Основы теории упругости
Лекция 2
Теория напряжений
Слайд 2
Внешние силы, которые действуют на твёрдое тело, можно разделить на две группы: поверхностные и массовые.
Поверхностные силы являются результатом взаимодействия двух тел. Примером поверхностных сил являются давление одного тела на другое при соприкосновении, давление здания на грунт, давление газа или жидкости на стенки сосуда и т. д.
Поверхностные силы характеризуются интенсивностью qv, т.е. величиной силы, приходящейся на единицу площади поверхности, на которой распределена эта сила. Интенсивность поверхностной силы также называется давлением. Размерность давления выражается в Н/м2 (или Па). Проекции (компоненты) давления qv на оси координат x, y, z обозначаются Xv, Yv, Zv, соответственно. Здесь ν – внешняя нормаль к поверхности тела, к которой приложена эта сила.
Массовые силы распределены по всей массе тела. Примером массовых сил являются сила тяжести, магнитные силы, силы инерции для тела, находящегося в движении, и т. д. Массовые силы, отнесённые к единице объёма (т. е. интенсивности массовых сил, называемые объёмными силами), также раскладывают на три проекции: X, Y, Z. Их размерность – Н/м3.
Проекция интенсивности внешней нагрузки считается положительной, если её направление совпадает с направлением соответствующей координатной оси. Поверхностные и массовые силы, так же как и параметры НДС, являются функциями координат точки.
В твёрдом теле всегда имеют место внутренние силы, которые выражают взаимодействие молекул между собой и обеспечивают существование твёрдого тела, его прочность. При действии на тело внешних сил оно деформируется. Вследствие этого возникают дополнительные внутренние силы.
Слайд 3
Для исследования возникающих в теле внутренних сил воспользуемся методом сечений, который применим к находящемуся в равновесии телу, нагруженному внешними силами (рис. 2.1).
Рисунок 2.1 – К определению понятия «метод сечений»
Мысленно рассечём тело произвольной плоскостью на две части A и B и отбросим часть B. Оставшаяся часть A также находится в равновесии под воздействием приложенных внешних сил F1, F2, F3,... и системы внутренних сил, распределённых по сечению и представляющих собой действие удалённой части B на часть A.
Выделим в плоскости сечения вокруг точки M элементарную площадку ΔA, весьма малую, по сравнению с размерами сечения, но довольно большую, по сравнению с расстояниями между отдельными молекулами тела.
Обозначим через ΔF главный вектор внутренних сил, пересекающих площадку ΔA. Тогда напряжением внутренних сил, или полным напряжением, pv в точке М тела на лежащей в плоскости сечения площадке ΔA с нормалью ν называется предел отношения
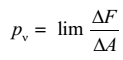
Аналогично можно определить полные напряжения в остальных точках этого и других сечений, проведённых через тело.
Полное напряжение является вектором: оно характеризуется величиной и направлением. В общем случае вектор полного напряжения наклонён к площадке ΔA, на которой он действует, и не совпадает с направлением нормали ν к площадке. Поэтому вместо полного напряжения рv удобнее рассматривать его составляющие в сечениях, параллельных координатным плоскостям.
Слайд 4
Для этого в окрестности точки O тела, нагруженного внешними силами, вырежем элементарный параллелепипед (рис. 2.2), рёбра dx, dy, dz, которого параллельны координатным осям x, y, z, а грани – параллельны координатным плоскостям xOy, xOz, yOz. На гранях этого параллелепипеда действуют полные напряжения, которые можно разложить на нормальную (нормальное напряжение) и касательную (касательное напряжение) составляющие к грани. В свою очередь, касательное напряжение можно разложить на две составляющие, параллельные координатным осям. В результате на каждой грани параллелепипеда действует по три напряжения – одно нормальное и два касательных. Напряжения обозначаются греческими буквами: σ − нормальные напряжения, τ − касательные напряжения.
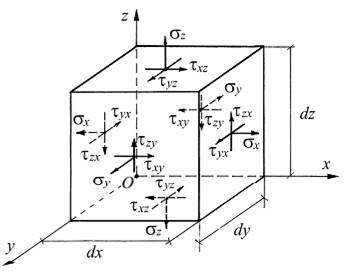
Рисунок 2.2 – Напряжения на гранях элементарного параллелепипеда
Первый индекс в обозначении напряжений указывает ось, параллельно которой направлено напряжение, а второй индекс – ось, параллельно которой направлена внешняя нормаль к грани параллелепипеда, на которой действует напряжение. Если сказать короче, то первый индекс указывает направление напряжения, а второй – площадку, на которой оно действует.
Примем следующее правило знаков для напряжений: для σ, если внешняя нормаль к площадке имеет положительное направление, то напряжение положительно. В случае τ, если его направление совпадает с положительным направлением соответствующей координатной оси. В соответствии с приведённым правилом знаков положительные нормальные напряжения являются растягивающими, а отрицательные – сжимающими. На рис. 2.2 показаны положительные направления напряжений. Напряжения, так же как и интенсивность поверхностной нагрузки, выражаются в Н/м2 (Па).
Совокупность напряжений, действующих на трёх взаимно перпендикулярных гранях параллелепипеда, – три нормальных напряжения (σx, σy, σz) и шесть касательных напряжений (τxy, τxz, τyz, τyx, τzx, τzy) – образует так называемый тензор напряжений, который характеризует напряжённое состояние в рассматриваемой точке O твёрдого тела.
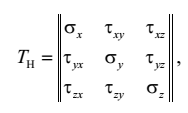(2.1)
Слайд 5
Дифференциальные уравнения равновесия (уравнения Навье)
Выясним, каким условиям должны быть подчинены напряжения на гранях элементарного параллелепипеда, чтобы каждый элемент тела в своём взаимодействии с соседними элементами был в равновесии, а, следовательно, было в равновесии и всё тело.
Ввиду бесконечной малости параллелепипеда на рис. 2.2, принято, что напряжения во всём его объёме остаются неизменяемыми (однородное напряжённое состояние). В действительности компоненты тензора напряжений на параллельных гранях, отстоящих друг от друга на бесконечно малом расстоянии, отличаются одно от другого на бесконечно малую величину. Таким образом, как бы ни были близки грани элементарного объёма, имеет место приращение напряжений, пропорциональное расстоянию между гранями и равное частному дифференциалу этого напряжения. Поэтому на рис. 1.4 изображено уточнённое распределение напряжений на гранях параллелепипеда.
Рисунок 2.3 – Компоненты тензора напряжений, параллельные оси х
Рассмотрим напряжения, параллельные оси х: σx, σy, σz.
Если на левой грани элемента с координатой х = 0 принять напряжение σx, то на правой грани, имеющей координату dx, функция σx получит приращение 
, равное частному дифференциалу этой функции по аргументу x. В итоге на правой грани параллелепипеда будет напряжение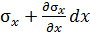 
.
Аналогично рассуждая, получим выражения для касательных напряжени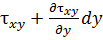й: 
и 
, а также для напряжений, параллельных осям y и z.
Кроме напряжений, на параллелепипед действуют массовые силы, компоненты которых на оси координат будут следующие:
X dx dy dz, Y dx dy dz, Z dx dy dz
Для тела, находящегося в равновесии, должны удовлетворяться шесть уравнений статики: три уравнения проекций сил на оси координат и три уравнения моментов этих сил относительно координатных осей.
Слайд 6
Уравнения равновесия проекций сил имеют вид:
(2.2)
Полученные три дифференциальных уравнения равновесия называются уравнениями Навье.
Если для параллелепипеда аналогично расписать три уравнения статики для моментов, то получим соотношения закона парности касательных напряжений:
Согласно этому закону по двум взаимно перпендикулярным площадкам составляющие касательных напряжений, перпендикулярные линиям пересечения этих площадок, равны между собой. Следует отметить, что следствием закона является симметрия тензора напряжений относительно главной диагонали.
Таким образом, вследствие парности касательных напряжений, вместо девяти неизвестных компонент тензора напряжений, которые характеризуют напряжённое состояние в точке тела и являются функциями координат этой точки, остаётся только шесть:
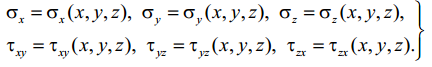(2.3)
Для отыскания шести неизвестных функций напряжений (2.3) имеются только три дифференциальных уравнения равновесия (2.2). Отсюда следует важный вывод: так как число неизвестных напряжений превышает число уравнений равновесия Навье, то задача теории упругости оказывается статически неопределимой. Недостающие уравнения можно получить, лишь изучая деформации и учитывая физические свойства тела.
Слайд 7
Напряжения на наклонных площадках. Условия на поверхности
Для исследования напряжённого состояния во всех точках тела необходимо уметь находить напряжения на площадке, наклонённой к осям координат.
Внутри нагруженного тела выделим в виде тетраэдра Оabc элементарный объём бесконечно малых размеров (рис. 2.4).
Рисунок 2.4 – Наклонная площадка abc
Три взаимно перпендикулярные грани Оab, Оbc, Оca тетраэдра параллельны координатным плоскостям, а четвёртая грань abc представляет собой наклонную площадку.
Предположим, что на трёх координатных гранях тетраэдра известны все компоненты тензора напряжений. Необходимо найти компоненты Xν, Yν, Zν полного напряжения pν на любой наклонной площадке с нормалью ν, направляющие косинусы которой равны:
Обозначим площадь грани abc через ΔA, тогда площади остальных граней тетраэдра определяются как проекции площади грани abc на соответствующие координатные плоскости:
пл. Оbc=ΔA l; пл. Оca=ΔA m; пл. Оab=ΔA n
На рассматриваемый тетраэдр действуют следующие нагрузки:
– на координатных площадках – шесть компонент напряжения: σx, σy, σz, τxy, τyz, τzy;
– на площадке abc – три компоненты полного напряжения: Xν, Yν, Zν. Действие объёмных сил не учитывается.
Составим уравнения статики для тетраэдра Оabc. Проецируя все силы на оси координат, получаем три уравнения равновесия элементарного тетраэдра:
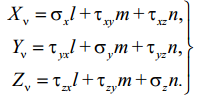(2.4)
Уравнения (2.4) позволяют определить компоненты полного напряжения pν на любой наклонной площадке с нормалью ν с помощью шести компонент тензора напряжений на площадках, параллельных координатным плоскостям.
Если наклонная площадка abc совпадает с поверхностью тела, то компоненты Xν, Yν, Zν полного напряжения pν являются компонентами давления qν от внешних сил, действующих на поверхности тела. Тогда уравнения (2.4) называются условиями на поверхности тела, так как в этом случае они связывают внешние силы с внутренними напряжениями.
Таким образом, при решении задачи теории упругости для равновесия тела под действием заданных внешних сил необходимо и достаточно, чтобы в каждой точке компоненты (2.1) тензора напряжений TH одновременно удовлетворяли дифференциальным уравнениям равновесия (2.2) внутри тела и условиям на его поверхности (2.4).
Главные напряжения. Инварианты тензора напряжений. Шаровой тензор и девиатор напряжений
Воспользуемся уравнениями (2.4) для вычисления напряжений на любой наклонной площадке в любой точке внутри тела, если известны шесть компонент (2.1) тензора напряжений на площадках, параллельных координатным плоскостям.
Полное напряжение на наклонной площадке определяется как геометрическая сумма компонент этого напряжения:
(2.5)
Разложим полное напряжение рν на составляющую σν по нормали к наклонной площадке (нормальное напряжение) и составляющую τν в плоскости наклонной площадки (касательное напряжение).
Нормальное напряжение σν равно сумме проекций компонент полного напряжения Xν, Yν, Zν на направление нормали ν к наклонной площадке (рис. 2.4):
Подставляя значения компонент Xν, Yν, Zν из (2.4), получаем:
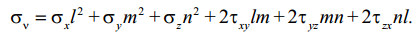(2.6)
Формула (2.6) позволяет определять нормальное напряжение на любой наклонной площадке с помощью шести компонент тензора напряжений на трёх площадках, параллельных координатным плоскостям.
Касательное напряжение на наклонной площадке определяется как геометрическая разность полного и нормального напряжений:
Слайд 9
Известно, что в каждой точке нагруженного тела существуют три взаимно перпендикулярные площадки, на которых касательные напряжения τxy, τyz, τzy равны нулю. Эти площадки называются главными, а направления нормалей к этим площадкам называются главными направлениями (или главными осями) тензора напряжений.
На главных площадках действуют главные нормальные напряжения σ1, σ2, σ3. Если главные напряжения различны, то имеется только три главных направления. Если два главных напряжения равны (например σ2=σ3), напряжённое состояние характеризуется осевой симметрией. Любая площадка, содержащая ось 1, − главная. Если все главные напряжения равны (σ1=σ2=σ3) напряжённое состояние характеризуется центральной симметрией. Любая площадка в данной точке является главной (случай гидростатического напряжённого состояния).
Из условия τν=0 с учётом (2.4), приходим к кубическому уравнению относительно искомого главного напряжения σ:
(2.7)
Решение этого уравнения в рассматриваемом случае даёт три вещественных корня (три главных напряжения): σ1, σ2, σ3.
Наибольший по абсолютной величине корень обозначается через σ1, а наименьший – через σ3. Поэтому σ1≥σ2≥σ3.
Слайд 10
Величины главных напряжений не зависят от положения координатных осей x, y, z, т. е. от выбора системы координат.
Поэтому коэффициенты уравнения (2.7)
(2.8)
должны сохранять постоянные значения при преобразовании осей координат, т. е. они являются инвариантами. Коэффициенты I1, I2, I3 называются, соответственно, первым, вторым и третьим инвариантом тензора напряжений.
Таким образом, инварианты тензора напряжений (2.8) – это характеристики напряжённого состояния, не зависящие от выбора системы координат.
Величина
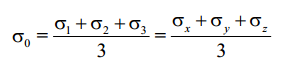(2.9)
называется средним нормальным напряжением.
Слайд 11
Инварианты тензора напряжений можно выразить через главные напряжения, для чего в формулах (2.8) касательные напряжения следует положить равными нулю, а нормальным напряжениям дать индексы 1, 2 и 3 главных напряжений. Тогда получим:
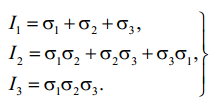(2.10)
Поэтому контролем правильности решения кубического уравнения (2.7) может служить равенство значений инвариантов I1, I2, I3, полученных по формулам (2.8) и (2.10).
В теории напряжений инварианты следует рассматривать как основные характеристики напряжённого состояния в точке. Компоненты же напряжений, как связанные с осями координат, являются вспомогательными характеристиками напряжённого состояния.
В сечении, делящем пополам углы между главными площадками, действуют главные касательные напряжения τ1, τ2, τ3:
Максимальным касательным напряжением называют величину
Для принятой выше нумерации осей наибольшее касательное напряжение равно полуразности наибольшего и наименьшего главного напряжения:
(2.11)
Это напряжение действует на площадке, которая делит пополам угол между площадками с наибольшим и наименьшим главными напряжениями.
Слайд 12
Так как тело по-разному сопротивляется равномерному всестороннему давлению и касательным напряжениям, то удобно представить тензор напряжений в виде суммы
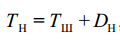(2.12)
где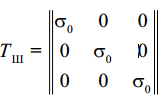 
- шаровой тензор напряжений, соответствующий среднему давлению в точке, а
- тензор, характеризующий напряжения сдвига в данной точке и называемый девиатором напряжений.
В заключение сформулируем следующее определение: напряжённым состоянием в точке называют совокупность напряжений, действующих по всевозможным площадкам, проведённым через эту точку.
Слайд 13
