ЛАБОРАТОРНАЯ РАБОТА
№ 26-1
по дисциплине «Цифровая обработка сигналов»
на тему:
«Анализ нерекурсивных цифровых фильтров
1-го и 2-го порядка»
Вариант № 5 а
Выполнил: студ. гр. БСС1402
Качан А.П.
Проверил: проф.
Волчков В. П.
(Осенний семестр)
Москва 2016
Цель работы
Провести экспериментальный анализ нерекурсивных (трансверсальных) цифровых фильтров (ЦФ) 1-го и 2-го порядка; исследовать частотные и временные характеристики цифровых фильтров, а также их взаимосвязь со значениями коэффициентов (параметров) ЦФ.
Выполнение домашнего задания
Исходные данные варианта
Исходные данные для расчетов и построение разностного уравнения полного ЦФ 1-го порядка приведены в таблице 1.
| № варианта | a1 | a2 | b0 | b1 | b2 | 
| 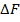 , Гц , Гц
|
| 7а | 0.4 | 0 - 8000 |
Табл. 1. Таблица исходных данных.
Записать разностное уравнение и системную функцию нерекурсивного ЦФ 1-го порядка.
| (1) |
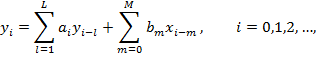
где { al } и { bm } – совокупности коэффициентов ЦФ, { xi-m } и { yi-l } – задержанные (соответственно на mи l периодов дискретизации) копии входного и выходного сигналов ЦФ
| (2) |
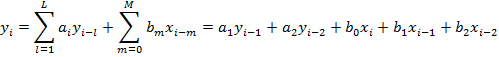
| (3) |

Системная функция H (z) ЦФ определяется отношением Z-преобразования отклика Y (z) и Z-преобразованием входного воздействия X(z).
| (4) |
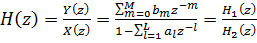
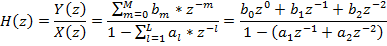

Системная функция ЦФ первого порядка в соответствии с исходными данными:
| (5) |
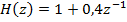
Изобразить структурную схему ЦФ.
Рекурсивные и полные ЦФ возможно реализовать в виде различных схем, отличающих методикой построения (программирования) и количеством использующихся элементов. При непосредственном (прямом) программировании по разностному уравнению строиться неканоническая структурная схема. Неканоническая схема для исследуемого фильтра приведена на рис. 1.
Рис. 1. Структурная схема цифрового нерекурсивного фильтра 1-го порядка.
(b0 =1; b1 = 0.4)
Рассчитать и построить импульсную реакцию и амплитудно-частотную характеристику ЦФ.
Выведем формулу и построим график реакции ЦФ 1-го порядка на единичный
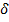 -импульс.
-импульс.
| (6) |

Заменим в формуле (3) 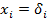 , тогда импульсная характеристика примет вид:
, тогда импульсная характеристика примет вид:
| (7) |
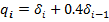
Подставив в (8) данные из таблицы 1, получаем импульсную реакцию ЦФ:

| (8) |
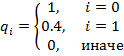
Рис. 2. Импульсная реакция цифрового фильтра 1-го порядка (b0=0;b1=0.4).
Рассчитать и построить амплитудно-частотную характеристику ЦФ.
Выведем формулу Амплитудно-частотной характеристики ЦФ 1-го порядка и построим ее график.
| (9) |
| (10) |

где 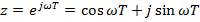
| (11) |

| (12) |
| (13) |
| (14) |
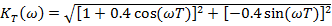 ;
;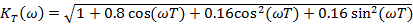 ;
;
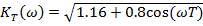
| (15) |
 (T=1.25*
(T=1.25* 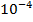 c,
c, 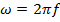 )
)
Рис. 3. АЧХ нерекурсивного цифрового фильтра 1-го порядка (b0 =0; b1 =0.4)






