Опр. Функция у = f (x) называется возрастающей на интервале (a<x<b), если для всех точек этого интервала при х2 > х1 выполняется неравенство f (x2) > f (x1).
Опр. Функция у = f (x) называется убывающей на интервале (a<x<b), если для всех точек этого интервала при х2 > х1 выполняется неравенство f (x2) < f (x1).
Простейшие элементарные функции
1. Линейная функция. 
График – прямая.
2. Степенная функция. 
График – парабола, гипербола.
3. Показательная функция. 
Графики всех показательных функций пересекают ось ординат в точке у=1.
4. Логарифмическая функция. 
5. Тригонометрические функции. y= cos x; y = sin x; y = tg x; y = ctg x.
6. Обратные тригонометрические функции. y= arccos x; y = arcsin x; y = arctg x; y = arcctg x.
Построение графиков функций
Опр. График функции у = f (x) – это множество всех точек (х,у) плоскости Оху, координаты которых связаны соотношением у = f (x), называемым уравнением графика функции.
Пределы, их свойства.
Опр. Пределом функции f(x) в точке х0 называется такое число b, если для любого (сколь угодно малого) числа Ɛ > 0 можно найти такое положительное число δ, что для любого числа х ≠ х0, удовлетворяющего неравенству 0< |х- х0 |< δ, выполняется отношение |у- b |< Ɛ.
Предел функции обозначается: 
Пример 5.1
Свойства пределов:
1. Если предел функции в точке х0 существует, то он единственный.
2. Предел постоянной равен этой постоянной. 
3. Предел алгебраической суммы нескольких функций равен алгебраической сумме пределов этих же функций.
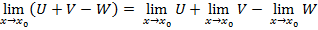
4. Предел произведения нескольких функций равен произведению пределов этих функций.
5. Предел частного двух функций равен частному пределов этих функций.
Следствия:
1. Постоянный множитель функции можно вынести за знак предела.
2. Предел многочлена и дробно-рациональных функций равен их значению в точке а, если а принадлежит области определения.
Опр. Функция f(x) называется бесконечно малой (бм), если предел функции, при х стремящимся к а, равен 0.
Опр. Функция f(x) называется бесконечно большой (бб), если предел функции, при х стремящимся к а, равен бесконечно большому числу или бесконечности.
Свойства:
1. Сумма нескольких бм(бб) величин равна бм(бб).
бм+бм+бм=бм бб+бб+бб=бб
2. Произведение бм(бб) на число с равно бм(бб).
бм · с = бм бб · с = бб
3. Произведение бм(бб) величин есть величина бм(бб).
бм · бм · бм=бм бб · бб · бб=бб
4. Сумма числа с и бм(бб) величин равна бм(бб).
бм + с = бм бб + с = бб
5. Частное некоторого числа с и бм равно бб.
6. Частное некоторого числа с и бб равно бм.
Замечательные пределы
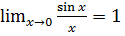- первый замечательный предел.
– второй замечательный предел.
Нахождение пределов.
Пример 6.1
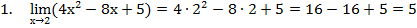
Очень часто при нахождении пределов дробно-рациональных функций получаются числовые неопределённости: 
В таких случаях для вычисления пределов функций выполняют равносильные преобразования алгебраических выражений:
1. Неопределённость 
раскрывается делением числителя и знаменателя на старшую степень аргумента (переменной).
Пример 6.2
2. Неопределённость 
раскрывается несколькими способами в зависимости от функции:
а) Разложить числитель и знаменатель на множители, сократить в полученную дробь на множитель стремящийся к нулю.
Пример 6.3
1) 3х2 + 10х – 8 = 0
3х2 + 10х – 8 = 3(х - 
)(х + 4) = (3х - 2)(х +4)
2) 
3) 
Ответ: 
б) Умножить числитель и знаменатель на множитель сопряжённый числителю или знаменателю, преобразовать полученное выражение и сократить на общий множитель стремящийся к нулю.
Опр. Сопряжёнными называются выражения, если они имеют противоположный знак действия.
(а + в) 
(а - в)
(а + в)(а - в) = 
Пример 6.4
Ответ: 2.
в) Для раскрытия неопределённости используют следующие отношения основанные на замечательных пределах, если х 
0, то под знаком предела можно выполнять равносильные замены: sin α = α, tg α = α, arcsin α = α, arctg α =α, ln(1 +α) = α.
Пример 6.5
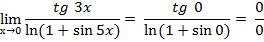
Ответ: 
