Интегрирование и дифференцирование
Решение алгебраических уравнений
Интегрирование и дифференцирование
Интегрирование и дифференцирование функций в пакете Mathcad осуществляется с использованием кнопки Calculus на панели инструментов.
Решение алгебраических уравнений
Численное решение систем уравнений в Mathcad. При этом должно быть задано некоторое начальное приближение для тех переменных, значение которых необходимо найти. Основываясь на этих начальных данных, Mathcad будет последовательно уточнять решение до тех пор, пока не подберет наиболее точные значения.
Решающий блок состоит из нескольких компонент, следующих на листе в строго определенном порядке:
1. Начальное приближение (присваивание начальных значений переменным).
2. Директива Given, которую необходимо набрать с клавиатуры.
3. Уравнения, которые необходимо решить. Уравнения вводятся в обычной математической форме, но вместо простого знака равенства используется оператор логического равенства (вводится путем нажатия Ctrl+=).
4. Обращение к функции Find. Аргументами функции являются имена переменных, относительно которых решается система. Функция возвращает вектор значений, где первый элемент соответствует первой переменной в списке аргументов, второй элемент — второй переменной и т. д. При этом решение системы может быть найдено как при помощи численного (знак «=»), так и с использованием символьного процессоров системы (знак «®»).
Пример 1. Решим систему нелинейных уравнений:
Данная система имеет два решения. Найдем одно из них (рис. 1) с начальным приближением x = 0; y = 0.
Рис. 1. Решение системы алгебраических уравнений в Mathcad
Последняя запись — вектор (–1; –2) есть значение, которое вернула функция Find, то есть одно из решений системы. Найти второе решение можно, если взять другое начальное приближение x = 2; y = 2. Тогда функция Find вернет вектор (2; 4).
В Mathcad существует возможность одновременно найти несколько решений. Для этого система уравнений и начальные приближения должны быть переписаны в векторной форме (рис. 2). Каждая переменная будет вектором, содержащим столько компонент, сколько решений находится. Допустим, что в уравнении присутствует выражение x*x. Если x = (x 1; x 2) — вектор, то 
. Нам же необходим результат поэлементного перемножения 
. Для этого существует специальная операция, записываемая как 
.
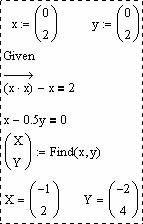
Рис. 2. Пример одновременного поиска нескольких решений
Изменения коснулись и части получения результата. В данном случае функция Find вернет вектор из двух элементов, которые мы обозначили как X и Y. Каждый из этих элементов есть вектор значений x или y для решений. Соответственно первое решение — (–1; –2); второе решение — (2; 4).
Также решение алгебраического уравнения в Mathcad может быть осуществлено с помощью функции root. Для этого необходимо задать начальное значение поиска неизвестной переменной этого уравнения. Затем привести уравнение к виду 
и определить в среде Mathcad полученную функцию 
. Решение уравнения будет найдено при помощи встроенной функции root(f(x),x). Если же уравнение имеет несколько решений, то необходимо задать интервал поиска корня в виде дополнительных параметров функции root: root(f(x),x,a,b), где a, b — границы интервала. Причем значения f (a) и f (b) должны иметь разный знак.
Решение задачи определения корней полинома в Mathcad осуществляется при помощи встроенной функции polyroots(v), где v — вектор-столбец коэффициентов полинома, первым элементом которого является свободный член полинома, вторым — коэффициент при x 1 и т. д.
Аналитическое решение систем уравнений в Mathcad. Данное решение используется для получения решений в общем виде. Обычно при этом система уравнений записывается только с использованием буквенных обозначений переменных, без конкретных чисел. Для получения аналитического решения (рис. 3, 4) используется оператор аналитического вычисления «®» вместо оператора числового вычисления «=».
Рис. 3. Пример аналитического решения системы нелинейных уравнений
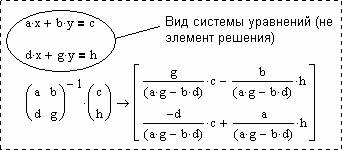
Рис. 4. Пример аналитического решения системы линейных уравнений
Следует обратить внимание, что здесь при решении системы нелинейных уравнений в блоке Given/Find уже нет необходимости указывать начальные приближения, поскольку решение идет не численными, а символьными методами (используется ядро математической системы Maple).
