В данном разделе лекции мы рассмотрим наиболее часто используемые команды, позволяющие выполнять над объектами (функциями, выражениями, рядами и.т.д) вычисления и преобразования, относящиеся к одному из разделов математики - математическому анализу. Многие из этих функций имеют как активную, так и пассивную (инертную) формы, которые различаются начертанием первой буквы имени команды (строчные - для активных команд, прописные - для инертных команд).
| Операции и функции математического анализа. | |
| Вычисление сумм рядов. | |
| < B> | Вычисление произведений. |
| Дифференцирование выражений. | |
| >Дифференциальный оператор. | |
| < B> | Вычисление интегралов. |
| Вычисление пределов функций. | |
| Разложение функции в ряд в виде степенного многочлена | |
| < B> | Разложение функции в ряд Тейлора |
| < B> | Разложение функции нескольких переменных в ряд Тейлора |
| < B> | Ассимптотическое разложение функции в ряд. |
| < B> | Позволяет найти экстремум выражения. |
| < B> | Определяет минимум функции. |
| Определяет максимум функции | |
| < B> | Исследует выражение на непрерывность. |
| < B> | Определяет точки, в которых нарушается непрерывность функции. |
| < B> | Находит особые (сингулярные) точки выражения. |

| Вычисление сумм рядов. |
Применение систем символьной математики особенно эффектно при решении задач математического анализа.
Вычисление суммы f(m)+f(m+1)+...+f(n-1)+f(n) является распространенной операцией математического анализа.
Для вычисляемой и инертной форм вычисления сумм служат следующие функции:
| sum(f,k) | sum(f,k=m..n) | sum(f,k=alpha) |
| Sum(f,k) | Sum(f,k=m..n) | Sum(f,k=alpha) |

| где: f-функция, задающая члены суммируемого ряда, k-индекс суммирования, m и n-целочисленные пределы изменения k, alpha-RootOf-выражение. Значение n может приниматься бесконечным, тогда для n используется константа infinity. |
Дополнительные возможности по работе с суммами обеспечивает инструментальный пакет sumtools.

| Вычисление произведений. |
Аналогичным образом для произведений членов f(i) некоторой последовательности, например вида f(m)*f(m+1)*...*f(n-1)*f(n) используются следующие функции:
| product(f,k) | product(f,k=m..n) | product(f,k=alpha) |
| Product(f,k) | Product(f,k=m..n) | Product(f,k=alpha) |

| Обозначение параметров этих функций и их назначение соответствуют приведенным для функции вычисления сумм. |

| Дифференцирование выражений. |
Вычисление производных функций n-го порядка -одна из самых распространенных задач математического анализа. Для ее реализации Maple V имеет следующие основные функции:
| diff(F,x1,x2,...,xn) | Diff(F,x1,x2,...,xn) |
| diff(F,[x1,x2,...,xn]) | Diff(F,[x1,x2,...,xn]) |
Здесь F -дифференцируемое алгебраическое выражение, в частности, функция F(x1,x2,...,xn) ряда переменных, по которым производится дифференцирование.
Функция Diff является инертной формой вычисляемой функции diff и может использоваться для естественного воспроизведения производных в документах.
Первая из этих функций (в вычисляемой и в инертной форме) вычисляет частные производные для выражения F по переменным x1,x2,...,xn. В простейшем случае diff(F(x),x) вычисляет первую производную функции F(x) по переменной x. При n большем 1 вычисления производных выполняются рекурсивно, например diff(f(x,y),x,y) эквивалентно diff(diff(f(x,y),x),y).
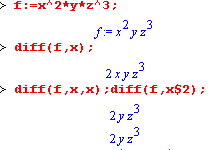
| Оператор $ можно использовать для вычисления производных высокого порядка. Для этого после имени соответствующей переменной ставится этот оператор и указывается порядок производной, например diff(f(x),x$4). |

| Дифференциальный оператор. |
Для создания функции с производными может также использоваться дифференциальный оператор D. Порою он позволяет создавать более компактные выражения, чем функции diff и Diff.

| Дифференциальный оператор можно записывать в следующих формах: D(f) или D[i](f), где параметр f-выражение или имя функции. i-положительное целое число, выражение или последовательность. |

| Оператор D(f) просто вычисляет имя производной от f. В форме D(f)(x) этот оператор подобен diff(f(x),x). |

| Вычисление интегралов. |
Для вычисления неопределенных и определеных интегралов Maple V предоставляет следующие функции:
| int(f,x) | int(f,x=a..b) | int(f,x=a..b,опция) |
| Int(f,x) | Int(f,x=a..b) | Int(f,x=a..b,опция) |
Здесь: f -подынтегральная функция,
x -переменная, по которой выполняются вычисления,
a и b - нижний и верхний пределы интегрирования (эти пределы могут быть и аналитическими выражениями, и бесконечностью, обозначаемой как infinity)
опция -опционально заданное условие.
По умолчанию команда интегрирования проверяет выражение на непрерывность в области интегрирования и вычисляет интеграл как сумму отдельных определенных интегралов на промежутках непрерывности функции. Опция continuous отключает этот режим и вычисляет интеграл как разность значений первообразной подынтегральной функции в точке начала и конца промежутка интегрирования.
Еще одна опция CauchyPrincipalValue вычисляет несобственные интегралы первого и второго рада в смысле главного значения Коши.
Если Maple не может найти замкнутую форму выражения для определенного интеграла, то команда интегрирования в области вывода повторяет саму себя. В подобных случаях можно вычислить значение определенного интеграла численным способом с помощью команды evalf(). Синтаксис подобной конструкции следующий:
evalf(int(f,x=a..b));
evalf(Int(f,x=a..b));
evalf(Int(f,x=a..b, digits, flag));
где digits задает число значащих цифр при вычислении приближенного значения интеграла,
flag - параметр, позволяющий явно задать метод численного интегрирования.

| При численном интегрировании по умолчанию используется квадратурная формула Кленшо-Куртиса (Clenshaw-Curtis). Если в подынтегральном выражении встречается сингулярность, то применяется специальная методика символьного анализа для ее разрешения. Для задач с неустранимыми сингулярностями используется адаптивный метод двойных экспоненциальных квадратур. Параметр flag, явно задающий метод численного интегрирования, может принимать значения, представленные в таблице: |
| Значения параметра flag. | |
| Значение | Смысл |
| _Ccquad | Применяется только квадратура Кленшо-Куртиса без вызова процедуры обработки сингулярности. |
| _Dexp | Применяется адаптивный метод двойных экспоненциальных квадратур. |
| _Ncrule | Применяется метод квадратурной формулы Ньютона-Кортеса, являющийся методом фиксированного порядка, и не эффективен для высоких точностей. |
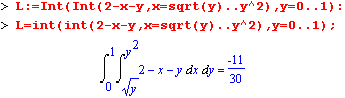
| Функции int и Int могут использоваться для вычисления кратных интегралов. Для этого они используются неоднократно. В пакете student имеются дополнительные функции интегрирования, которые дополняют уже описанные возможности. |

| Вычисление пределов функций. |
Для вычисления предела функции f в точке x=a используются следующие функции:
| limit(f,x=a) | limit(f,x=a,dir) |
| Limit(f,x=a) | Limit(f,x=a,dir) |

| Здесь: f-алгебраическое выражение, x-имя переменной, а- точка, в которой ищется предел (может быть бесконечность (как положительная, так и отрицательная)) dir -опция, указывающая на направление поиска предела (left-слева, right-справа, real-в области вещественных значений, complex-в области комплексных значений). |

| Разложение функции в ряд. |
Система Maple предлагает множество функций для разложений функций во всевозможные ряды. Познакомимся с некоторыми из них.
Команда series() дает разложение функции в форме степенного многочлена в окрестности некоторой точки. Её синтаксис:
series(выражение, условие)
series(выражение, условие, n)

| выражение- разлагаемое выражение, условие- уравнение вида x=a или имя переменной (например, x) n - неотрицательное число, задающее число членов ряда (по умолчанию = 6, можно переустановить системной переменной Order) |
Если в качестве параметра условие задано имя переменной, то будет построено разложение функции в рад по этой переменной в области точки с ее нулевым значением. Задав условие в виде равенства x=a, будем получать разложение функции по переменной x в окрестности точки x=a.
Остаточная погрешность при разложении функции в степенной ряд задается членом вида O(xn). При точном разложении этот член отсутствует. В общем случае для его удаления можно использовать функцию convert(выражение, polynom).
Для разложения функции в широко распространенный ряд Тейлора используется команда taylor(). Ее синтаксис:
taylor(выражение, усоловие, n)
Значения параметров команды те же, что и для команды series().
Для разложения в ряд Тейлора функции нескольких переменных используется команда mtaylor() в виде:
mtaylor(выражение, список) или mtaylor(выражение, список, n) или mtaylor(выражение, список, n, вес)
выражение - разлагаемое выражение
список - список имен или равенств
n - число, задающее порядок разложения
вес - список целых чисел, задающий "вес" каждой переменной списка - второго параметра команды.
Для вычисления ассимптотического разложения функции (в виде ряда)используется команда asympt() в форме:
asympt(f, x) или asympt(f, x, n)
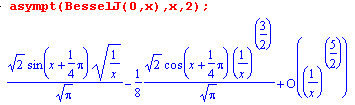
| f- функция переменной x или алгебраическое выражение x - имя переменной, по которой производится разложение n- положительное целое число (порядок разложения) |
Помимо указанных выше Maple имеет множество функций для иных разложений в ряд. Например в пакете расширения numapprox имеется функция laurent(), позволяющая получить разложение в ряд Лорана, функция chebyshev() дает разложение в форме полиномов Чебышева. Для использования в вычислениях разложений функций в ряды по ортогональным полиномам можно воспользоваться пакетом orthopoly, расширенные средства по реализации степенных разложений сосредоточены в пакете расширений powseries.

| Поиск экстремумов, анализ функций не непрерывность. |
Фуекция extrema() позволяет найти экстремумы выражения или функции, а также вывести координаты точек экстремумов. Её синтаксис
extrema(expr, условия, переменная, 'nv');
expr - выражение, экстремум которого следует найти,
условия - ограничения (по области и др.) задаются в виде множества уравнений или неравенств,
переменные - переменные, по которым ищется экстремум, задаются в виде множества (необязательный параметр)
'nv' - имя переменной, которой будут присваиваться координаты точек экстремума (необязательный параметр).
Для поиска максимального и минимального значений функции или выражения в Maple предназначены функции maximize () и minimize(). Их синтаксис:
minimize(expr, vars, опция);
maximize(expr, vars, опция);
expr - выражение, экстремум которого следует найти,
vars - список или множество переиенных
опция - параметр, указывающий область изменения независимых переменных выражения.
-
Параметр опция может принимать значения: 'infinity' - поиск максимума или минимума выполняется по всей числовой прямой, или представляет собой множество уравнений вида x=a..b, определяющих область изменения независимых переменных.
Функция iscont() позволяет исследовать выражение (функцию) на непрерывность. Синтаксис этой команды:
iscont(expr, x=a..b)
iscont(expr, x=a..b,'closed')
expr - выражение, исследуемое на непрерывность,
x - независимая переменная
a..b - промежуток изменения независимой переменной
'closed' - параметр, указывающий, что конечные точки также должны проверяться.
Если выражение непрерывно, возвращается логическое значение true, иначе - false.
Другая функция discont() позволяет определить точки, в которых нарушается непрерывность функции f(x). Она вычисляет все точки в пределах изменения x от минус бесконечности до плюс бесконечности. Обращение к этой команде:
discont(f(x),x)
Многие операции, например, интегрирования и дифференцирования, чувствительны к особенностям функций, в частности, к ее разрывам и особым точкам. Команда singular(expr, vars) позволяет найти особые (сингулярные) точки выражения expr, в которых оно испытывает разрывы.






