Перечень обязательных практических работ.
| № п/п | Наименование обязательной практической работы | Форма/место выполнения |
| 1. | Практическая работа 1. «Вычисление производных функций.» | Проводится в аудитории |
| 2. | Практическая работа 2. «Вычисление неопределенных и определенных интегралов» | Проводится в аудитории |
| 3. | Практическая работа 3. «Вычисление вероятностей событий. Характеристики случайных величин» | Проводится в аудитории |
| Практическая работа 4. «Составление дискретных и интервальных статистических рядов. Построение гистограммы. Статистические оценки.» | Проводится в аудитории |
Перечень вопросов промежуточной аттестации.
1. Предел функции.
2. Теоремы о пределах
3. Методы нахождения пределов.
4. Производная функции и её геометрический и физический смыслы.
5. Формулы дифференцирования.
6. Дифференциал функции.
7. Первообразная. Неопределенный интеграл и его свойства.
8. Методы интегрирования.
9. Определенный интеграл. Площадь криволинейной трапеции.
10. Методы нахождения определенного интеграла.
11. Определение вероятности события.
12. Основные теоремы теории вероятностей. Теорема сложения.
13. Теорема умножения вероятностей.
14. Формула полной вероятности.
15. Формулы Байеса.
16. Повторные независимые испытания. Схема Бернулли.
17. Случайные величины и срособы их задания.
18. Математическое ожидание случайной величины.
19. Дисперсия и среднеквадратическое отклонение случайной величины.
20. Понятие ковариации и корреляции.
21. Выборочный метод. Выборка.
22. Дискретный статистический ряд. Полигон.
23. Интервальный статистический ряд. Гистограмма и алгоритм её построения.
24. Точечные статистические оценки генеральных параметров.
25. Интервальная статистическая оценка математического ожидания.
26. Статистические гипотезы.
27. Правило принятия статистической гипотезы.
28. Основы корреляционно-регрессионного анализа.
Задания для домашних контрольных работ (при их наличии в рабочем учебном плане).
Контрольное задание №1.
Номера задач, соответствующие каждому варианту, определяются последней цифрой электронного пропуска. Допустим, пропуск имеет номер 12304057, следовательно, студенту необходимо решить все задачи, номера которых заканчиваются цифрой7, т.е. задачи 7, 17, 27, 37,....
В задачах 1-10 найти заданные пределы.
1.  2.
2. 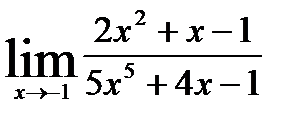
3.  4.
4. 
5.  6.
6. 
7.  8.
8. 
9.  10.
10. 
В задачах 11-20 требуется найти производные заданных функций.
11. y=(x5+8x)sin2x 12. y=e2x(x3+  )
)
13. y=(x+1)2tg8x 14. y= 
15. y=x3·ctg2x 16. y= 
17. y=  18. y=lncos3x
18. y=lncos3x
19. y=aeax+xe-ax 20. y=ex/a·sin(x/a)
В задачах 21-30 требуется найти дифференциалы заданных функций.
21. y=  22. y=cos32x
22. y=cos32x
23. y= x·3x 24. y=ln(lnx)
25. y=lntg2x 26. y=sin 3x+5
27. y=ln3(x/3) 28. y=ln(sinx+2cosx)
29. y=sin2x·cos2x 30. y=  + arctg
+ arctg 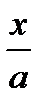
В задачах 31-40 требуется исследовать с помощью производной заданные функции на возрастание, убывание, экстремумы, промежутки выпуклости и вогнутости графика функции и наличие точек перегиба.
31. y =  32. y =
32. y = 
33. y =  34. y =
34. y = 
35. y =  36. y =
36. y = 
37. y =  38. y =
38. y = 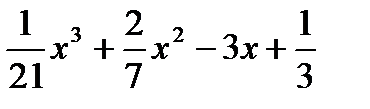
39. y =  40. y =
40. y = 
В задачах 41-50 требуется найти частные производные, частные и полные дифференциалы заданных функций.
41. z=arctg  42. z=ex/y
42. z=ex/y
43. z=sin2(x+y)-sin2x 44. z=x3y
45. z=x2·sin  46. z=
46. z= 
47. z=arcsin  48. z=
48. z= 
49. z=  ·sin
·sin  50. z=e(x/y)·lny
50. z=e(x/y)·lny
Контрольное задание № 2
В задачах 41-50 требуется вычислить указанные неопределенные интегралы способом непосредственного интегрирования.
41. 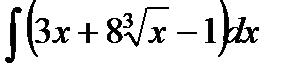 42.
42. 
43.  44.
44. 
45.  46.
46. 
47.  48.
48. 
49. 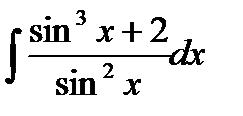 50.
50. 
В задачах 51-60 вычислить указанные неопределенные интегралы методом подстановки.
51. 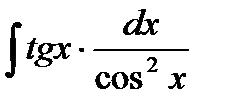 52.
52. 
53.  54.
54. 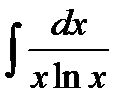
55.  56.
56. 
57. 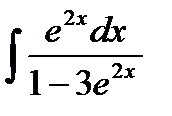 58.
58. 
59.  60.
60. 
В задачах 61-70 вычислить указанные определенные интегралы.
61. 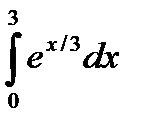 62.
62. 
63.  64.
64. 
65.  66.
66. 
67.  68.
68. 
69.  70.
70. 
Индивидуальное задание №3
В задачах 71-80 найти вероятности событий, используя классическое определение вероятности и теоремы сложения и умножения.
71. В аптеке работают 4 мужчины и 12 женщин. По табельным номерам наудачу отобраны 8 человек. Какова вероятность того, что среди отобранных лиц окажутся 3 мужчины?
72. Брошены две игральные кости. Какова вероятность выпадения на двух костях в сумме 6 очков?
73. Из пяти карточек с буквами А,Б,В,Г,Д наугад одна за другой выбираются три и располагаются в ряд в порядке появления. Какова вероятность, что получится слово ДВА?
74. В цехе работают 6 мужчин и 4 женщины. По табельным номерам наудачу отобраны 7 человек. Найти вероятность того, что среди отобранных лиц окажутся 3 женщины.
75. В группе 12 студентов, среди которых 8 отличников. По списку наудачу отобраны 9 студентов. Найти вероятность того, что среди отобранных студентов 5 отличников.
76. На стеллаже библиотеки в случайном порядке расставлено 15 учебников, причем, 5 из них в переплете. Библиотекарь берет наудачу 3 учебника. Найти вероятность того, что хотя бы один из взятых учебников окажется в переплете.
77. В ящике 10 деталей, из которых 4 окрашены. Сборщик наудачу взял три детали. Найти вероятность того, что хотя бы одна из взятых деталей окрашена.
78. В читальном зале имеются 6 учебников по теории вероятностей, из которых три в переплете. Библиотекарь наудачу взял два учебника. Найти вероятность того, что оба учебника окажутся в перепрлете.
79. Студент знает 20 из 25 вопросов программы. Найти вероятность того, что студент знает предложенные ему экзаменатором 3 вопроса.
80. В мешочке содержится 10 одинаковых кубиков с номерами от 1 до 10. Наудачу извлекают по одному 3 кубика. Найти вероятность того, что последовательно появятся кубики с номерами 1, 2, 3, если кубики извлекают: а) без возвращения, б) с возвращением.
В задачах 81-90 найти математическое ожидание, дисперсию и среднее квадратическое отклонение дискретной случайной величины X, заданной законом распределения.
81.
| xi | 0,5 | 1,0 | 1,7 | 2,0 | 2,4 | 2,8 |
| pi | 0,1 | 0,15 | 0,2 | 0,22 | 0,18 | 0,15 |
82.
| xi | 1,5 | 3,2 | 5,1 | 7,4 | 8,9 | 10,5 |
| pi | 0,05 | 0,09 | 0,15 | 0,21 | 0,29 | 0,21 |
83.
| xi | |||||||
| pi | 0,03 | 0,06 | 0,11 | 0,17 | 0,23 | 0,22 | 0,18 |
84.
| xi | ||||||||
| pi | 0,02 | 0,08 | 0,14 | 0,17 | 0,19 | 0,16 | 0,13 | 0,11 |
85.
| xi | 10,1 | 10,8 | 11,6 | 12,5 | 13,6 | 14,8 |
| pi | 0,12 | 0,15 | 0,19 | 0,23 | 0,17 | 0,14 |
86.
| xi | 10,1 | 10,3 | 10,5 | 10,6 | 10,8 |
| pi | 0,1 | 0,2 | 0,3 | 0,2 | 0,2 |
87.
| xi | 0,5 | 1,5 | 2,6 | 3,8 | 4,3 |
| pi | 0,1 | 0,2 | 0,4 | 0,2 | 0,1 |
88.
| xi | -4,7 | -4,5 | -4,2 | -3,9 | -3,4 |
| pi | 0,11 | 0,13 | 0,22 | 0,24 | 0,3 |
89.
| xi | ||||||
| pi | 0,15 | 0,20 | 0,25 | 0,20 | 0,15 | 0,05 |
90.
| xi | |||||||
| pi | 0,12 | 0,13 | 0,18 | 0,20 | 0,15 | 0,17 | 0,05 |
Индивидуальное задание №4.
Составить интервальный вариационный ряд распределения и построить гистограмму и кумуляту для следующих данных:
| 11,70 | 9,03 | 13,70 | 12,31 | 6,68 | 5,60-k/10 | 8,06 | 12,90 |
| 7,35 | 7,76 | 12,30 | 5,91 | 6,23 | 12,37 | 11,50 | 8,69+k/10 |
| 11,35 | 13,70 | 11,11 | 9,74 | 12,33 | 14,75 | 6,86 | 12,90 |
| 13,90 | 9,70 | 12,00 | 13,56 | 6,67 | 12,75 | 15,33 | 9,73+N/10 |
| 11,00 | 15,30 | 9,50 | 11,99 | 14,40 | 10,36 | 13,00 | 10,60+N/10 |
| 9,75 | 10,79 | 14,10 | 12,05 | 11,25 | 15,67 | 14,67 | 15,95 |
| 15,21 | 16,00 | 12,41 | 9,02 | 16,20 | 9,32 | 8,81 | 10,11+k/10 |
| 13,57 | 10,32 | 13,85 | 13,60 | 16,60 | 15,05 | 12,97 | 13,60 |
| 9,21 | 17,00+k/10 | 12,80 | 17,60 | 10,81 | 16,95 | 9,85 | 10,70+N/10 |
| 14,90 | 15,95 | 13,40 | 16,80 | 6,96 | 12,03 | 12,00 | 11,50 |
| 12,90 | 7,39 | 16,10 | 9,35 | 13,75 | 8,80 | 13,01 | 8,64+(N+k)/10 |
| 11,80 | 10,48 | 15,85 | 11,56 | 12,56 | 11,67 | 12,27 | 12,07 |
| 10,51 | 12,09 | 12,31 | 9,76 |
Здесь N – число букв в ФИО; k - номер фамилии студента в журнале. Объем выборки определяется формулой:
n=100-[(N+k)/3], где [ ] означают целую часть числа. Число классов, величину частичного интервала, середины и границы частичных интервалов определять с точностью до тысячных.
По гистограмме определить моду Мо. По кумуляте определить медиану, квартили.
Рассчитать точечные оценки для генеральных параметров и интервальную оценку для математического ожидания.
Проверить гипотезу о нормальном распределении генеральной совокупности (χ2 Пирсона).
5. Форма аттестации – контрольная работа и дифференцированный зачёт вопросам в аудитории.
Список источников информации (методические указания, методические пособия, учебные пособия, учебники, интернет-ресурсы).
Основные источники:
1.1.Григорьев В П, Дубинская Т Н «Элементы высшей математики» 8-е издание Москва. Изд центр «Академия». 2013.
1.2.Григорьев В П, Сабурова Т Н «Сборник задач по высшей математике». Учебное пособие для СПО. Москва. Изд центр «Академия». 2010 год
1.3.Теория вероятностей и математическая статистика: учебник для студ. учреждений сред. проф. образования / М.С. Спирина, П.А. Спирин. – М.: Издательский центр «Академия», 2007. – 352 с. ISBN 978-5-7695-2768-
Дополнительные источники:
1.4.Филимонов Е.В. Математика для ССУЗов. – Ростов на Дону, Феникс, 2005.
1.5.Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. – М.: Высшая школа, 2004.
1.6.Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Высшая школа, 2009.
1.7.Колмогорова А.В. Математика. – СПб.: Петровский колледж, 2012
Преподаватель А.В. Гармашов
Старший методист Н.Н. Скрыпникова






