Кулачковым называется механизм, имеющий в составе кулачок – ведущее звено с криволинейной рабочей поверхностью. Такие механизмы применяются для преобразования равномерного вращательного движения ведущего звена – кулачка в возвратное (колебательное) движение ведомого звена – толкателя. На рис.1 показана схема дискового кулачкового механизма со штанговым толкателем. Закон движения толкателя теоретически может быть любым, поскольку задается профилем кулачка. Вследствие этого кулачковые механизмы воспроизводят наиболее разнообразные классы законов движения. Этим и объясняется их широкое распространение в технике, особенно в машинах-автоматах, несмотря на большое удельное давление от динамических нагрузок, прежде всего инерционных, в высших кинематических парах (пара кулачок – толкатель) и повышенный износ этих пар. Последнее обстоятельство ограничивает возможности применения кулачковых механизмов в тяжелонагруженных и быстроходных устройствах.
При проектировании профиля кулачка обычно задаются законом движения толкателя. Выбор закона движения определяется, главным образом, теми требованиями, которые предъявляет технологический процесс к движению толкателя. В качестве требуемого закона движения можно принять определенный тип кривой перемещения, скорости или ускорения. Динамика кулачковых механизмов в основном определяется законами изменения ускорений (так как с ускорением толкателя связаны пропорциональные ему и массе толкателя силы инерции, учитывать которые приходится при расчете замыкающих пружин, при определении напряжений в деталях механизма и т.д.), поэтому обычно в качестве закона движения толкателя задаются кривой (или уравнением) относительных ускорений толкателя. Технологические соображения в большинстве случаев заставляют обращаться к сложным законам движения.
В диаграмме аналога ускорения толкателя приведен закон движения толкателя. Представленные в виде безразмерных коэффициентов относительных значений ускорений νа и угла поворота Ку на фазе удаления. Для приведенных примеров в начале, а также в промежуточных положениях ускорение может изменяться скачком на конечную величину (мягкий удар за счет мгновенного изменения силы инерции). Для ряда законов ускорение меняется скачком в конце фазы удаления, в других случаях скачки на графиках ускорений могут отсутствовать: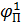 
= 
.
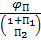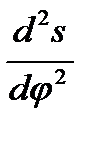
jп jвв jo jнв
jпI
а 1
| j, t |
0 а2 360о
jпI = jп /(1+ a 1/ a 2)
Рис.1. Диаграмма аналога ускорения толкателя
Кулачковый механизм со штанговым толкателем (рис.2) преобразует равномерное вращение кулачка 1 (n1 = const) в возвратно-поступательное движение штангового толкателя 2. Закон движения толкателя определяется профилем кулачка.
При движении толкателя на фазе подъема сила реакции R12 между кулачком и роликом 3 толкателя направлена под углом Ɵ к скорости толкателя ν2 (направление скорости совпадает с осью штанги). Этот угол называется углом давления. Обратный ход толкателя происходит под действием пружины 4. Величина допускаемого угла давления Ɵдоп лимитирует коэффициент полезного действия (КПД) механизма и определяет размеры кулачка.
Закон движения толкателя задан графиком функции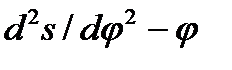 
аналога линейного ускорения толкателя, приведенным на рис.3.
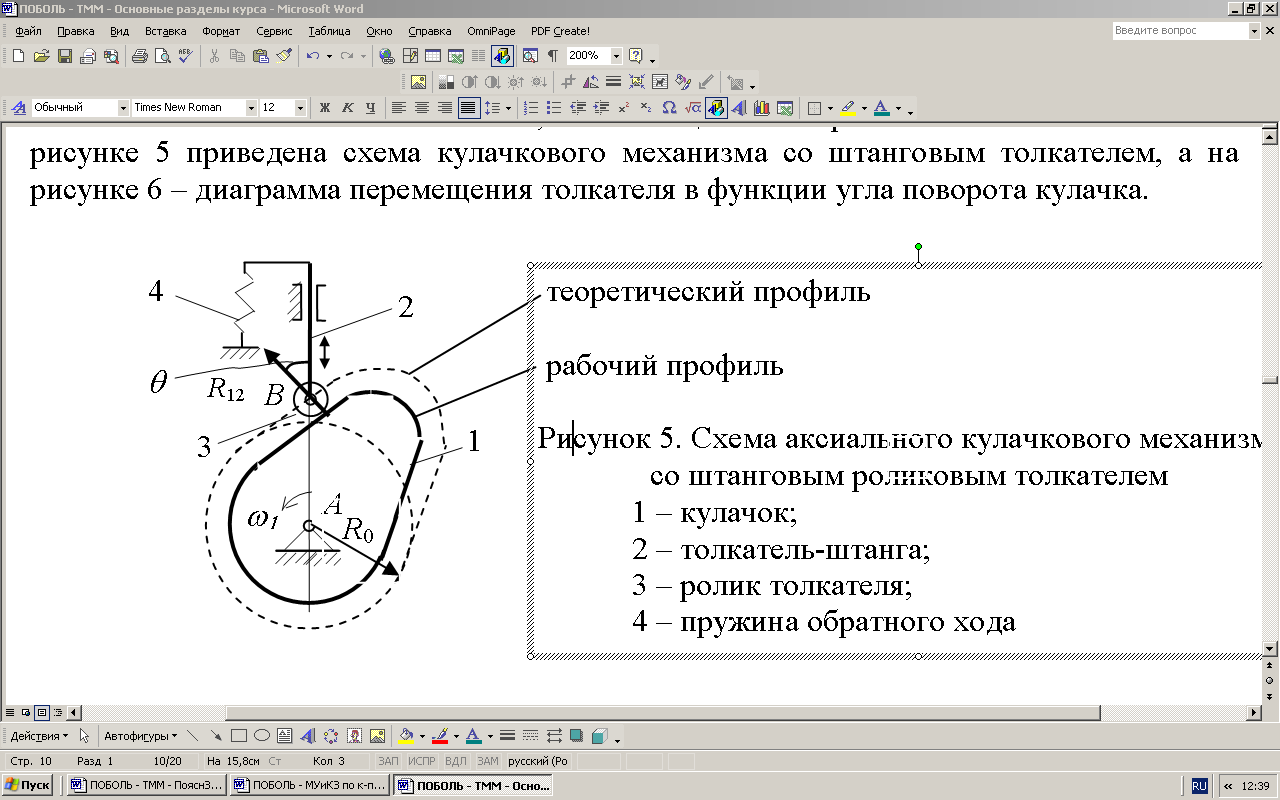
| теоретический профиль рабочий профиль |
Рис.2. Схема кулачкового механизма со штанговым толкателем
Цикл движения толкателя, соответствующий одному обороту кулачка φ1 = 3600, в общем случае разделяется на 4 фазы: подъема (удаления), верхнего выстоя, опускания (приближения) и нижнего выстоя, чему соответствуют фазовые углы подъема φП, верхнего выстоя φВВ, опускания φО и нижнего выстоя φНВ, показанные на циклограмме (рис.3). Законы движения выходного звена на фазах его подъема и опускания, определяемые формой профиля кулачка, и величины фазовых углов задаются по кинематическим и динамическим условиям.
| jнв |
| Н |
| j1 = 3600 |
| j |
| 0 |
| jо |
| jп |
| jвв |
| s |
Рис.3. Циклограмма перемещения толкателя
Закон движения толкателя определяется формой и размерами выступающей части теоретического профиля кулачка, который отстоит от рабочего профиля на величину радиуса ролика толкателя rрол. При отсутствии ролика на конце толкателя теоретический профиль совпадает с рабочим.
При проектировании кулачкового механизма законы движения толкателя, определяющие профиль кулачка, задают (выбирают) в зависимости от требований технологического процесса, при этом возможны два варианта:
- толкатель должен перемещаться по определенному закону, связанному с выполнением технологической операции (например, рабочие органы в станках-автоматах, швейных машинах);
- толкатель должен перемещаться на заданную величину хода за определенное время, при этом закон движения не влияет на технологический процесс.
В первом случае закон движения толкателя однозначно определяется технологическим процессом, а во втором случае его выбирает конструктор с учетом заданных условий (ход, скорость вращения кулачка). При прочих равных условиях выбирается такой закон перемещения толкателя, при котором обеспечиваются наилучшие условия работы механизма.
В большинстве случаев при выборе этих законов стремятся задать движение толкателя с наименьшими ускорениями, что позволяет работать с наименьшими нагрузками. В результате уменьшаются силы инерции и реакций в кинематических парах и, как следствие, их износ, потери на трение, а также вибрации и шум при эксплуатации машин.
Рассмотрим типовые законы движения толкателя, ограничившись фазой подъема, поскольку на фазе опускания зависимости аналогичны. При равномерном вращении кулачка ω1 = const, текущий угол поворота (в радианах) в функции времени t равен φ = ω1t, а длительность подъема зависит от величины фазового угла подъема φП и равна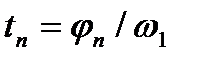 
.
1. Закон движения с постоянной скоростью и бесконечными значениями ускорения толкателяв начале и конце фазы(рис.6 а).
Диаграммы перемещения 
, скорости 
и ускорения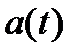 
толкателя для этого закона показаны на рис.5,а. Перемещение возрастает линейно до максимума, равного ходу толкателя H, при постоянной скорости 
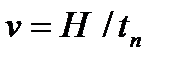.В начале и конце фазы, когда скорость резко изменяет свое значение, ускорение теоретически бесконечно 
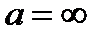, а практически, вследствие влияния упругости звеньев оно конечно, но достигает очень больших значений. Это явление называется «жестким ударом» и вызывает появление значительных нагрузок, что обуславливает интенсивный износ механизмов. Применение таких законов нежелательно, а в быстроходных механизмах недопустимо.
2. Закон движения с постоянным ускорением (рис.6,б).
В начале, середине и конце фазы подъема происходит «мягкий удар», когда ускорение резко изменяет свое значение, при этом в середине фазы сменяется и знак ускорения, равного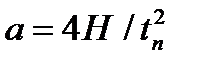 
. Скорость толкателя в начале фазы равна нулю и возрастает линейно до значения 
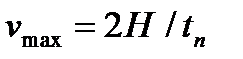в середине фазы, а затем падает линейно до нуля в конце фазы подъема. Перемещение изменяется по параболической зависимости
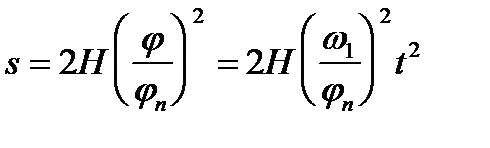при 
;
при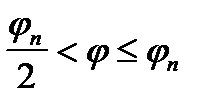 
. (4)
3. Закон косинусоидального ускорения (рис.6,в).
При движении толкателя с косинусоидальным ускорением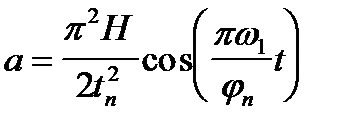 
, как и в случае постоянного ускорения, в точках разрыва кривой ускорения наблюдается «мягкий удар», связанный с экстремальными нагрузками. При этом реальные значения ускорений и нагрузок значительно превосходят расчетные из-за влияния колебательных процессов, связанных с упругостью звеньев.
4. Закон синусоидального ускорения (рис.6,г).
Наилучшие условия работы при законе с синусоидальным ускорением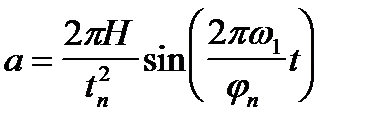 
, когда происходит плавное изменение ускорения от нуля до максимума и далее вновь до нуля.Законы с плавным изменением ускорения (синусоидальный, описанные полиномами) оптимальны для кулачковых механизмов, в связи с чем кулачки с такими профилями получили наибольшее распространение.
В быстроходных кулачковых механизмах, где закон перемещения толкателя задается технологическим процессом, в целях снижения ускорений вводят специальные участки профиля кулачков для плавного перехода к движению из состояния покоя на фазах выстоя и обратно.
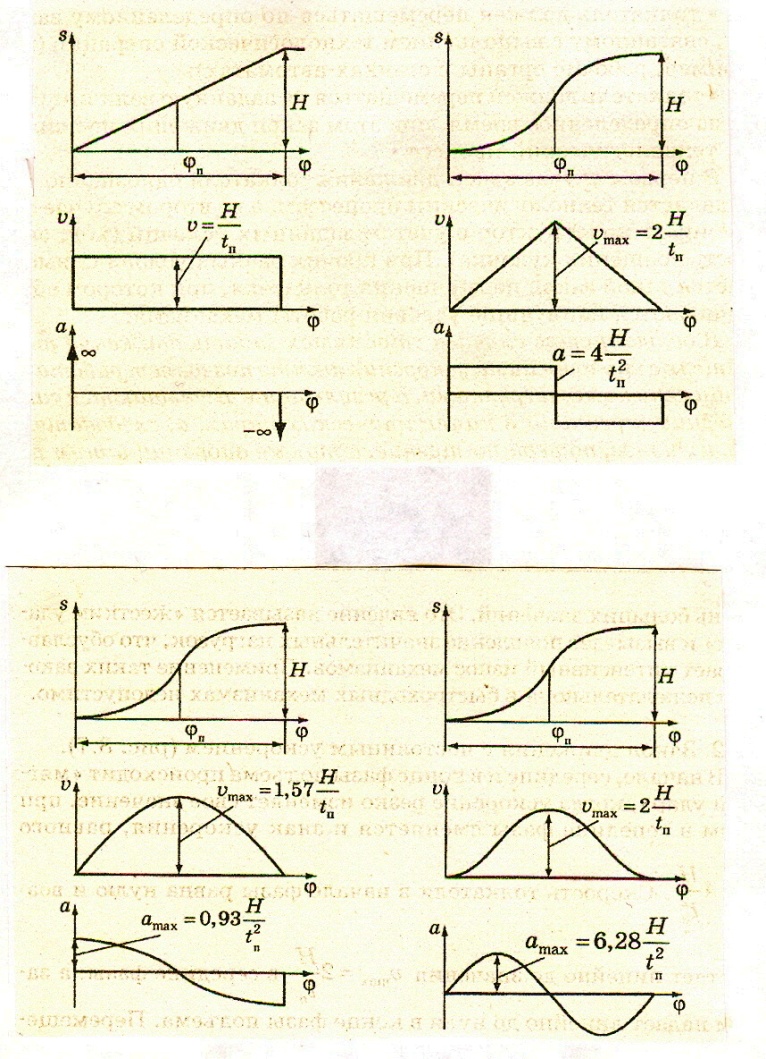
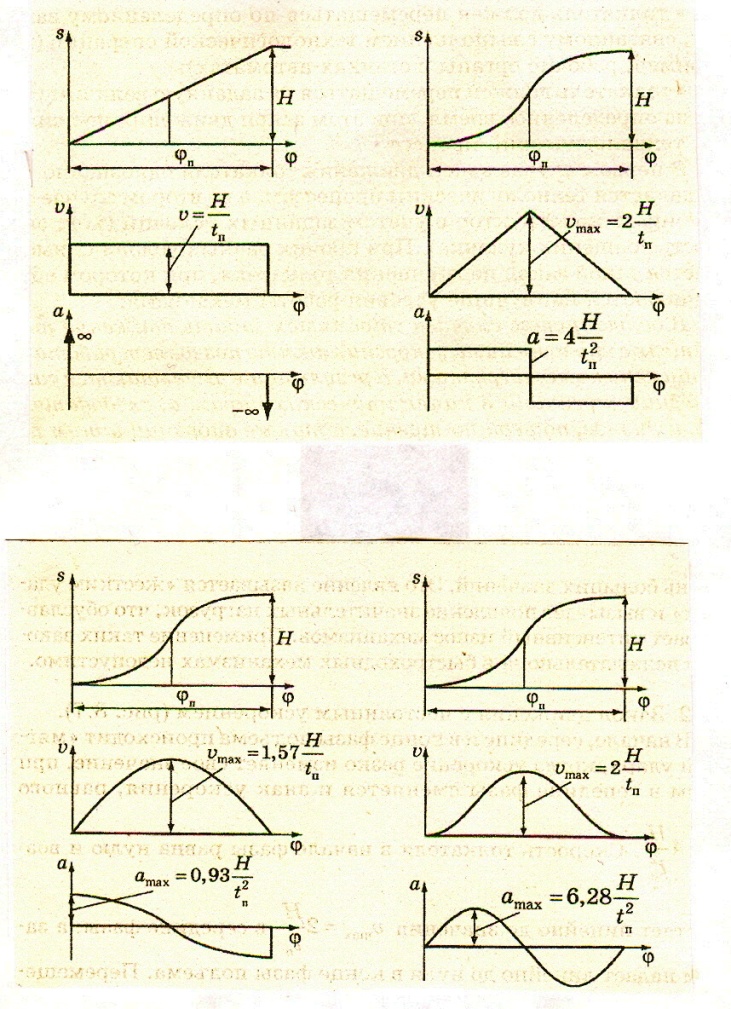
Рис.4. Диаграммы кинематических характеристик толкателей на фазе подъёма
а – с постоянной скоростью; б – с постоянным ускорением; в – с косинусоидальным ускорением; г – с синусоидальным ускорением.
В настоящем курсовом проекте задан параболический закон движения толкателя при постоянстве ускорения (пункт 2, рис.6 б).
Характер движения толкателя определяется формой и размерами теоретического профиля кулачка, который отстоит от рабочего профиля на величину радиуса ролика толкателя rрол. При анализе характеристик движения выходного звена за нулевое положение принимается начало фазы его подъема (при выходе из контакта с участком минимального радиуса теоретического профиля R0), соответствующее крайнему нижнему положению. При повороте кулачка, вращающегося с постоянной частотой n1, на фазовый угол подъема φп толкатель перемещается в крайнее верхнее положение. Величина перемещения из крайнего нижнего в крайнее верхнее положение носит название хода толкателя: линейного H или углового ψ. С этого момента начинается участок профиля кулачка постоянного радиуса, соответствующий фазе верхнего выстоя с фазовым углом φвв, - при прохождении этого угла поворота кулачка толкатель неподвижен. Затем следует фаза опускания с фазовым углом φo - на участках подъема и опускания кулачек имеет профиль переменного радиуса. Наконец, следует фаза нижнего выстоя с фазовым углом φнв,которой соответствует участок профиля кулачка постоянного радиуса - наименьшего.
Размеры кулачка определяются величиной минимального радиуса R0 теоретического профиля (называемого также центровым, поскольку он является геометрическим местом положения центров ролика толкателя при обкатке его по рабочему профилю кулачка), c которой суммируются соответствующие величины линейного перемещения толкателя.
Величина минимального радиуса R0 назначается из условия выполнения заданных ограничений по углу давления кулачка на ведомое звено – толкатель по уравнению (5). Углом давления Ɵ называется угол, образованный реактивной силой R12, с которой кулачек действует на толкатель, и скоростью v2 центра ролика толкателя (смотри рисунки). Угол давления Ɵ на ведомый толкатель равен углу между нормалью n-n к теоретическому профилю кулачка в точке контакта с осью ролика толкателя и осью штангового толкателя или перпендикуляром к оси коромысла - эти направления соответствуют направлениям скоростей соответствующих толкателей. Как видно из приведенных рисунков (см. рис.3 и 4), с увеличением углов давления растут составляющие реактивной силы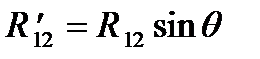 
, вызывающей прижатие штангового толкателя к направляющим или коромыслового толкателя к оси его поворота. В результате действия этого прижатия возникают силы трения между толкателем и направляющими или осью, определяющие величину коэффициента полезного действия (КПД) кулачкового механизма.
2.3. Определение величины минимального радиуса. Профилирование кулачка. Определения максимального значения угла давления Ɵmax кулачка на толкатель и сравнение его с допускаемым Ɵдоп..
Величина КПД связана с габаритами кулачкового механизма и прежде всего с величиной минимального радиуса RO теоретического профиля кулачка и кинематическими характеристиками механизма (линейным перемещением s и аналогом линейной скорости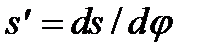 
). Установлена зависимость угла давления от этих параметров, которая для центральных механизмов со штанговым толкателем имеет вид
,=> 
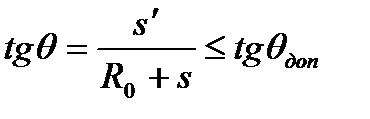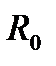(5)
где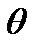 
- текущее значение угла давления, град;
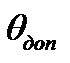- значение допускаемого угла давления, град;
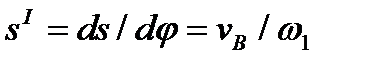- аналог скорости толкателя в некотором положении, мм;
s - перемещение толкателя в этом положении, мм;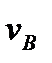 
- скорость толкателя (оси ролика), мм/с;
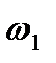- угловая скорость кулачка, рад/с;
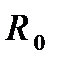- минимальный радиус теоретического профиля, мм.
Наименьшие значения КПД при одинаковых размерах имеют место в центральных механизмах со штанговым толкателем, а наибольшие - в коромысловом.
По заданному закону ускорения толкателя для ряда положений механизма рассчитываем и строим (путем последовательного интегрирования диаграммы ускорения) диаграммы изменения скорости и перемещения центра ролика толкателя в функции угла поворота кулачка φ и времени t и определяем величины перемещений и скорость для расчетных положений:
ω1 =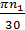 
сек-1,
где n1 – частота вращения кулачка.
ω1 =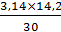 
= 1,5 сек-1
Находим длительность подъема фазового угла:
tn =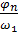 
с,
где φn – фазовый угол поворота кулачка,
ω1 – угловая скорость кулачка
tn =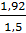 
= 1,28 с
В начале, середине и конце фазы подъема происходит «мягкий удар», когда ускорение резко изменяет свое значение, при этом в середине фазы сменяется и знак ускорения, равного:
a =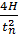 
,
где Н – ход толкателя,
tn – длительность подъема фазового угла
a =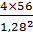 
= 136,7 мм/с2
Скорость толкателя в начале фазы равна нулю и возрастает линейно до значения νmax = 
в середине фазы, а затем падает линейно до нуля в конце фазы
νmax =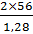 
= 87,5 мм/с
Рассчитываем диаграмму перемещения толкателя, которая изменяется по параболической зависимости:
S2 = 2H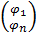 
2,
где Н – ход толкателя,
φ1 – фазовый угол поворота в рабочем ходе,
φn – фазовый угол поворота кулачка
S2 = 2×56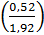 
2 = 8,2 мм
Определяем величину максимального радиуса R0 с учетом закона движения толкателя и величины допускаемого угла давления Ɵдоп:
tg Ɵ =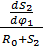 
≤ tg Ɵдоп
Из этого условия выводим максимальный радиус R0
R0 =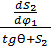 
= 
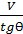- s,
где tgƟ – угол давления,
S2 – зависимость перемещения толкателя,
dS2|dφ1 – ускорение профиля кулачка
R0 =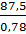 
- 8,2 = 104 мм
где Ɵ принимается за максимальный угол давления, который равен допускаемому углу давления Ɵдоп
