пределение параметров парной линейной регрессии

Рассмотрим методику построения уравнения парной регрессии в случае, когда функция отклика y предполагается линейно зависящей от фактора x. Если случайные величины X и Y представлены выборочными совокупностями (x 1, x 2,…, xn), и (y 1, y 2,…, yn) их опытных значений, объема n каждая, то для наглядности рекомендуется построить точки Mi (i =1,2,…, n) с координатами (xi, yi), на плоскости xy. Расположение этих точек даёт представление о виде искомой зависимости y = f (x). Если коэффициент детерминации близок к единице, то расположение точек должно подтвердить предположение о линейной зависимости случайных величин X и Y, и уравнение регрессии следует искать в виде уравнения прямой: y = kx + b, (1) параметры k и b которой подлежат определению. Подбор параметров k и b осуществляется, как обычно, на основе так называемого «метода наименьших квадратов» (МНК). Суть метода наименьших квадратов состоит в отыскании таких значений параметров k и b уравнения (1), которые будут минимизировать функцию Необходимое условие экстремума функции многих переменных – это равенство нулю её частных производных по переменным k и b в точке экстремума. Дифференцируя функцию S (k, b) по k и по b, и приравнивая полученные частные производные к нулю, получим следующую систему для нахождения неизвестных a и b: (2) Решив систему (2), находим значения неизвестных k и b, которые минимизируют функцию S (k, b) и могут быть представлены в следующем виде: (3) Напомним, что черта над каждой из переменных означает ее среднее выборочное. Подставляя найденные значения k и b в выражение (1), получаем искомое уравнение регрессии.

Метод наименьших квадратов является одним из наиболее распространенных и наиболее разработанных вследствие своей простоты и эффективности методов оценки параметров линейныхэконометрических моделей. Вместе с тем, при его применении следует соблюдать определенную осторожность, поскольку построенные с его использованием модели могут не удовлетворять целому ряду требований к качеству их параметров и, вследствие этого, недостаточно “хорошо” отображать закономерности развития процесса .

Рассмотрим процедуру оценки параметров линейной эконометрической модели с помощью метода наименьших квадратов более подробно. Такая модель в общем виде может быть представлена уравнением (1.2):

y_t = a₀ + a₁ х_1t +...+ a_n х_nt + ε_t.

Исходными данными при оценке параметров a₀ , a₁ ,..., a_n является вектор значений зависимой переменной y = (y₁, y₂,..., y_T )' и матрица значений независимых переменных

в которой первый столбец, состоящий из единиц, соответствует коэффициенту модели .

Название свое метод наименьших квадратов получил, исходя из основного принципа, которому должны удовлетворять полученные на его основе оценки параметров: сумма квадратов ошибки модели должна быть минимальной.

Коэффициент детерминации (R2{\displaystyle R^{2}} — R-квадрат) — это доля дисперсии зависимой переменной, объясняемая рассматриваемой моделью зависимости, то есть объясняющими переменными. Более точно — это единица минус доля необъяснённой дисперсии (дисперсии случайной ошибки модели, или условной по факторам дисперсии зависимой переменной) в дисперсии зависимой переменной. Его рассматривают как универсальную меру зависимости одной случайной величины от множества других. В частном случае линейной зависимости R2{\displaystyle R^{2}} является квадратом так называемого множественного коэффициента корреляциимежду зависимой переменной и объясняющими переменными. В частности, для модели парной линейной регрессии коэффициент детерминации равен квадрату обычного коэффициента корреляции между y и x. Истинный коэффициент детерминации модели зависимости случайной величины y от факторов x определяется следующим образом:

R2=1−V(y|x)V(y)=1−σ2σy2,{\displaystyle R^{2}=1-{\frac {V(y|x)}{V(y)}}=1-{\frac {\sigma ^{2}}{\sigma _{y}^{2}}},}

где V(y|x)=σ2{\displaystyle V(y|x)=\sigma ^{2}} — условная (по факторам x) дисперсия зависимой переменной (дисперсия случайной ошибки модели).

В данном определении используются истинные параметры, характеризующие распределение случайных величин. Если использовать выборочную оценку значений соответствующих дисперсий, то получим формулу для выборочного коэффициента детерминации (который обычно и подразумевается под коэффициентом детерминации):

R2=1−σ^2σ^y2=1−SSres/nSStot/n=1−SSresSStot,{\displaystyle R^{2}=1-{\frac {{\hat {\sigma }}^{2}}{{\hat {\sigma }}_{y}^{2}}}=1-{\frac {SS_{res}/n}{SS_{tot}/n}}=1-{\frac {SS_{res}}{SS_{tot}}},}

где SSres=∑t=1net2=∑t=1n(yt−y^t)2{\displaystyle SS_{res}=\sum _{t=1}^{n}e_{t}^{2}=\sum _{t=1}^{n}(y_{t}-{\hat {y}}_{t})^{2}} — сумма квадратов остатков регрессии, yt,y^t{\displaystyle y_{t},{\hat {y}}_{t}} — фактические и расчётные значения объясняемой переменной.

SStot=∑t=1n(yt−y¯)2=nσ^y2{\displaystyle SS_{tot}=\sum _{t=1}^{n}(y_{t}-{\overline {y}})^{2}=n{\hat {\sigma }}_{y}^{2}} — общая сумма квадратов.

y¯=1n∑i=1nyi{\displaystyle {\bar {y}}={\frac {1}{n}}\sum _{i=1}^{n}y_{i}}

В случае линейной регрессии с константой SStot=SSreg+SSres{\displaystyle SS_{tot}=SS_{reg}+SS_{res}} , где SSreg=∑t=1n(y^t−y¯)2{\displaystyle SS_{reg}=\sum _{t=1}^{n}({\hat {y}}_{t}-{\overline {y}})^{2}} — объяснённая сумма квадратов, поэтому получаем более простое определение в этом случае — коэффициент детерминации — это доля объяснённой суммы квадратов в общей:

R2=SSregSStot{\displaystyle R^{2}={\frac {SS_{reg}}{SS_{tot}}}}

Необходимо подчеркнуть, что эта формула справедлива только для модели с константой, в общем случае необходимо использовать предыдущую формулу.

Оценка статистической значимости параметров уравнения регрессии

С помощью МНК мы получили лишь оценки параметров уравнения регрессии, которые характерны для конкретного статистического наблюдения (конкретного набора значений x и y). Если оценку параметров произвести по данным другого статистического наблюдения (другому набору значений x и y), то получим другие численные значения , . Мы предполагаем, что все эти наборы значений x и y извлечены из одной и той же генеральной совокупности. Чтобы проверить, значимы ли параметры, т.е. значимо ли они отличаются от нуля для генеральной совокупности используют статистические методы проверки гипотез.
В качестве основной (нулевой) гипотезы выдвигают гипотезу о незначимом отличии от нуля параметра или статистической характеристики в генеральной совокупности. Наряду с основной (проверяемой) гипотезой выдвигают альтернативную (конкурирующую) гипотезу о неравенстве нулю параметра или статистической характеристики в генеральной совокупности. В случае если основная гипотеза окажется неверной, мы принимаем альтернативную. Для проверки этой гипотезы используется t -критерий Стьюдента.
Найденное по данным наблюдений значение t -критерия (его еще называют наблюдаемым или фактическим) сравнивается с табличным (критическим) значением, определяемым по таблицам распределения Стьюдента (которые обычно приводятся в конце учебников и практикумов по статистике или эконометрике). Табличное значение определяется в зависимости от уровня значимости (a) и числа степеней свободы, которое в случае линейной парной регрессии равно (n -2), n -число наблюдений.
Если фактическое значение t -критерия больше табличного (по модулю), то основную гипотезу отвергают и считают, что с вероятностью (1-a) параметр или статистическая характеристика в генеральной совокупности значимо отличается от нуля.
Если фактическое значение t -критерия меньше табличного (по модулю), то нет оснований отвергать основную гипотезу, т.е. параметр или статистическая характеристика в генеральной совокупности незначимо отличается от нуля при уровне значимости a.
Для параметра b критерий проверки имеет вид:
,
где - оценка коэффициента регрессии, полученная по наблюдаемым данным;
– стандартная ошибка коэффициента регрессии.
Для линейного парного уравнения регрессии стандартная ошибка коэффициента вычисляется по формуле:
.

Числитель в этой формуле может быть рассчитан через коэффициент детерминации и общую дисперсию признака-результата: .
Для параметра a критерий проверки гипотезы о незначимом отличии его от нуля имеет вид:
,
где - оценка параметра регрессии, полученная по наблюдаемым данным;
– стандартная ошибка параметра a.
Для линейного парного уравнения регрессии:
.
Для проверки гипотезы о незначимом отличии от нуля коэффициента линейной парной корреляции в генеральной совокупности используют следующий критерий:
, где r_yx - оценка коэффициента корреляции, полученная по наблюдаемым данным; m _r – стандартная ошибка коэффициента корреляции r_yx.
Для линейного парного уравнения регрессии:
.
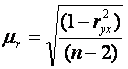В парной линейной регрессии между наблюдаемыми значениями критериев существует взаимосвязь: t _{( b =0)} = t _{(r=0 )}.

дной из центральных задач эконометрики является прогнозирование значений зависимой переменной при определенных значениях объясняющих переменных. Различают точечное и интервальное прогнозирование. При этом возможно предсказать условное математическое ожидание зависимой переменной (т.е. ср. значение), либо прогнозировать некоторое конкретное значение (т.е. индивидуальное).

Пусть имеется уравнение регрессии . Точечной оценкой М(У│Х=хр) = р = . Так как и имеют нормальное распределение (в силу нормальности ), то 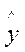р является случайной величиной с нормальным распределением.

,

М( р) = М() =

D( р) = D() + D() + xp2D() + 2cov(, )xp = +

+ xp2 -2xp = ( + xp2 - 2 xp )│ =

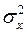= ( + - 2 xp + xp2) = .

- стандартная ошибка положения линии регрессии. Так как она минимальна при хр = , то наилучший прогноз находится в центре области наблюдений и ухудшается по мере удаления от центра.

Случайная величина имеет распределение Стьюдента с (n-2) степенями свободы. Поэтому, задавая = Р( <tкр(, n-2)), можно построить доверительный интервал для М(У│Х = хр), то есть положения линии регрессии (рис. 1.): ()

Рис. 1. Доверительные интервалы положения линии регрессии – сплошная линия и индивидуального значения – пунктирная линия.

Фактические значения у варьируются около среднего значения р. Индивидуальные значения у могут отклоняться от р на величину случайной ошибки . Пусть yi - некоторое возможное значение у при хр. Если рассматривать yi как случайную величину У, а р – как случайную величину Ур, то можно отметить, что:

Y ~ N(, Yp ~ N( ).

Y и Yp независимы и, следовательно, U = Y - Yp ~ N с параметрами

M(U) = 0; D(U) = .

Значит случайная величина, имеющая распределение Стьюдента с (n-2) степенями свободы. Аналогично строится доверительный интервал индивидуального значения.

Пример. Стандартная ошибкасреднего расчетного значения

.

При , . При , . Следовательно, и, т.к. , то и

.

Стандартная ошибка индивидуального расчетного значения

,

и .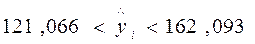

Фактические значения результативного признака отличаются от теоретических, рассчитанных по уравнению регрессии. Для сравнения используются величины отклонений, выраженные в процентах к фактическим значениям. Поскольку может быть как положительной, так и отрицательной величиной, ошибки аппроксимации для каждого наблюдения принято определять в процентах по модулю.

Для того чтобы иметь общее суждение о качестве модели из относительных отклонений по каждому наблюдению, находят среднюю ошибку аппроксимации как среднюю арифметическую простую.

.

Допустимый предел 8 – 10 %, при котором подбор модели к исходным данным считается хорошим.

Возможно и другое определение средней ошибки аппроксимации:

.

Рассчитаем среднюю ошибку аппроксимации для нашего примера.

 

 

№	y
		31,053	1,053	0,035
		67,895	2,105	0,030
		141,579	8,421	0,056
		104,737	4,737	0,047
		178,421	8,421	0,049
		104,737	4,737	0,047
		141,579	8,421	0,056
	0,322

 

Окончательно получим: , что говорит о хорошем качестве уравнения.

Выборочный коэффициент вариации определяется отношением выборочного среднего квадратического отклонения к выборочной средней, выраженным в процентах:

и .

Коэффициент вариации – безразмерная величина, удобная для сравнения величин рассеивания двух и более выборок, имеющих разные размерности. Совокупность данных считается однородной и пригодной для использования МНК и вероятностных методов оценок статистических гипотез, если значение коэффициента вариации не превосходит 35 %.

Для нашего примера:

,

.

Различают два класса нелинейных регрессий:

1. Регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам, например

§ полиномы различных степеней – , ;

§ равносторонняя гипербола – ;

§ полулогарифмическая функция – .

2. Регрессии, нелинейные по оцениваемым параметрам, например

§ степенная – ;

§ показательная – ;

§ экспоненциальная – .

Регрессии нелинейные по включенным переменным приводятся к линейному виду простой заменой переменных (линеаризация), а дальнейшая оценка параметров производится с помощью метода наименьших квадратов. Рассмотрим некоторые функции.

Парабола второй степени приводится к линейному виду с помощью замены: . В результате приходим к двухфакторному уравнению , оценка параметров которого при помощи МНК, приводит к системе следующих нормальных уравнений:

А после обратной замены переменных получим

(1.17)

Парабола второй степени обычно применяется в случаях, когда для определенного интервала значений фактора меняется характер связи рассматриваемых признаков: прямая связь меняется на обратную или обратная на прямую.

Равносторонняя гипербола приводится к линейному уравнению простой заменой: . Система линейных уравнений при применении МНК будет выглядеть следующим образом:

(1.18)

Аналогичным образом приводятся к линейному виду зависимости , и другие.

Несколько иначе обстоит дело с регрессиями нелинейными по оцениваемым параметрам, которые делятся на два типа: нелинейные модели внутренне линейные (приводятся к линейному виду с помощью соответствующих преобразований, например, логарифмированием) и нелинейные модели внутренне нелинейные (к линейному виду не приводятся).

К внутренне линейным моделям относятся, например, степенная функция – , показательная – , экспоненциальная – , логистическая – , обратная – .

К внутренне нелинейным моделям можно, например, отнести следующие модели: , .

Среди нелинейных моделей наиболее часто используется степенная функция , которая приводится к линейному виду логарифмированием:

,

где . Т.е. МНК мы применяем для преобразованных данных:

а затем потенцированием находим искомое уравнение.

Широкое использование степенной функции связано с тем, что параметр в ней имеет четкое экономическое истолкование – он является коэффициентом эластичности.

Коэффициент эластичности показывает, на сколько процентов измениться в среднем результат, если фактор изменится на 1%. Формула для расчета коэффициента эластичности имеет вид:

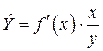. (1.19)

Так как для остальных функций коэффициент эластичности не является постоянной величиной, а зависит от соответствующего значения фактора , то обычно рассчитывается средний коэффициент эластичности:

. (1.20)

Приведем формулы для расчета средних коэффициентов эластичности для наиболее часто используемых типов уравнений регрессии:

Австралийский экономист А В Филлипс в 1958 году доказал, что между инфляцией и безработицей существует обратная связь При высоком безработице инфляция низкая и наоборот Эта взаимосвязь в общем виде и он отразил в кривиивих.

А В Филипс выяснил, что \"в Великобритании существует зависимость между скоростью изменения номинальной заработной платы и доли безработных в общей численности рабочей силы, такая зависимость оставалась сти ийкою на протяжении 1861-1957 лет \"-1957 років":

_{щ =} ^^{( Л} ₌ ^ ^ ^

И ^)

где ю - скорость изменения ставок заработной платы си и 5 - спрос и предложение и - доля безработных в общей численности рабочей силы, / - форма функции

Если учесть изменения стоимости жизни (в процентах) и обозначить его P, то зависимость будет иметь вид:

ю = f (u) kP

где k - положительная постоянная величина

Если k = 1, то формуле выражается зависимость между изменением реальной заработной платы ю, выраженной в процентах, и долей безработных u если k 1, это означает, что увеличение заработной платы не полностью компенсирует повышение цен и реальная заработная плата снижается

Кривые Е Энгеля

На основе изучения семейных расходов (бюджетов) Энгель сформулировал закономерность, названную его именем: отношение части доходов, предназначенной для закупки продуктов, к общему доходу изм меншуеться вместе с ростом доход.

На величину спроса на данный товар влияют различные факторы, но в первую очередь цена P и доход m В первом приближении спрос d можно рассматривать как функцию цены и дохода: d = f (P, m)

Спрос можно представить графически в трех измерениях как некоторую поверхность D (рис 65) Предположим, что цена является постоянной: P = P₁, тогда для этой цены спрос d = f (P₁, m) и является функцией дохода m На рис 65 изображением функций, для которых P = const, будут кривые, полученные путем пересечения поверхности D плоскостями, перпендикулярными к оси OP, на которой отложены величины цены P Это и есть кривые Энгеля

На рис 66 в двух измерениях представлены кривые Энгеля для постоянных P, P₂, P₃. Они выражают зависимость спроса от дохода в данной цены

Если мы предположим, что доход является постоянным: m = m₁, то спрос d = f (P, m₁) является функцией цены Изображением таких функций является кривые, которые образуются путем пересечения поверхности D плоскостями, перпендикулярными к оси Om

На рис 67 представлены кривые, выражающие зависимость спроса от цены за допущение, что доход является постоянным, равным соответственно m₁, m₂, m₃....

С помощью кривых Энгеля, составленных на основе семейных бюджетов, можно количественно оценить влияние роста национального дохода на увеличение потребления

Уравнение нелинейной регрессии, так же как и в линейной зависимости, дополняется показателями корреляции:

= 1- ; .

Величину R2 для нелинейных связей называют индексом детерминации, а R – индексом корреляции. Чем ближе значение R2 к 1, тем связь рассматриваемых признаков теснее, тем более надежно уравнение регрессии.

Если после преобразования уравнение регрессии (нелинейное по объясняющим переменным) принимает форму линейного парного уравнения регрессии, то для оценки тесноты связи может быть использован линейный коэффициент корреляции R yx = ryz, где z – преобразованная величина признака-фактора, например z = 1/ x или z = ln x.

Если преобразования в линейную форму связаны с результативным признаком (нелинейность по параметрам), то линейный коэффициент корреляции по преобразованным значениям признаков дает лишь приближенную оценку тесноты связи. Он численно не совпадает с R, R 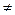r, так как r рассчитывается между ln y и ln x, а коэффициент детерминации использует суммы квадратов отклонений признака y, а не его логарифма.

R2 для нелинейной регрессии имеет тот же смысл, что и коэффициент детерминации.

Оценка существенности индекса корреляции производится так же, как и оценка надежности коэффициента корреляции. Индекс корреляции R используется для проверки существенности уравнения нелинейной регрессии в целом по F – критерию Фишера:

F = , где n – число наблюдений, р – число параметров при х.

Индекс детерминации R2 можно сравнивать с коэффициентом детерминации r 2 для обоснования возможности применения линейной функции. Чем больше кривизна линии регрессии, тем величина коэффициента детерминации r 2 меньше индекса детерминации R2. Близость этих показателей означает, что нет необходимости усложнять форму уравнения регрессии и можно использовать линейную функцию. Практически, если величина (R2 – r 2) 0,1, то предположение о линейной форме связи считается оправданным. В противном случае проводится оценка существенности различий R2, вычисленных по одним и тем же исходным данным, через t – критерий Стьюдента:

,

где 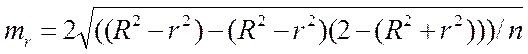- ошибка разности между R2 и r 2.

Если tнабл > tкр, то различия между рассматриваемыми показателями корреляции существенны и замена нелинейной регрессии уравнением линейной функции невозможно. Если t < 2, то различия между R и r несущественны, и, следовательно, возможно применение линейной регрессии, даже если есть предположение о некоторой нелинейности рассматриваемых соотношений признаков фактора и результата.

Если R2 и r 2 приблизительно равны, используют стандартную процедуру, известную под названием теста Бокса-Кокса. Тест включает следующие шаги:

1) определяется среднее геометрическое y в выборке;

2) пересчитываются наблюдения 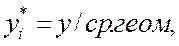где - пересчитанные значения для i-го наблюдения;

3) оценивается регрессия для 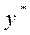вместо y и для логарифмической модели ln y * вместо ln y;

4) определяют величину , где z – отношение значений суммы квадратов отклонений в пересчитанных регрессиях, n – число наблюдений.

Эта статистика имеет распределение с 1-й степенью свободы. Если < кр(1, ), то разница значима. Модель с меньшей суммой квадратов отклонений обеспечивает лучшее соответствие.

(3.45)

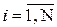- номер опыта;

j - номер объясняющей переменной;

Коэффициент эластичности показывает: на сколько единиц (либо процентов) в долях от среднего значения измениться выходная величина , если объясняющая переменная хj измениться на одну единицу (либо процент) в долях от среднего значения .

Таким образом, Э j измеряет чувствительность к вариации хj.

Замечание. В учебниках по эконометрике почему-то умалчивается вопрос: в долях от чего измеряются вариации и хj? Без этой информации определения для Э j становиться для студентов малопонятным.

 

Бета-коэффициент выражается формулой

(3.46)

Это 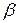– коэффициент отличается от коэффициента эластичности только масштабами нормировки хj и : вместо средних взяты их средние квадратические отклонения.

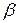– коэффициент показывает: на сколько % в долях от Sy измениться , если хj измениться на 1% в долях от .

(3.47)

 

Дельта-коэффициент определяется по формуле

 

(3.48)

 

Здесь – коэффициент парной корреляции между j -м фактором и зависимой переменой Y.

Дельта-коэффициент показывает долю влияния каждого фактора в суммарном влиянии всех факторов на зависимую переменную Y.

Построение модели множественной регрессии является одним из методов характеристики аналитической формы связи между зависимой (результативной) переменной и несколькими независимыми (факторными) переменными.

Модель множественной регрессии строится в том случае, если коэффициент множественной корреляции показал наличие связи между исследуемыми переменными.

Общий вид линейной модели множественной регрессии:

yi=

где yi – значение i-ой результативной переменной,

x1i…xmi – значения факторных переменных;

– неизвестные коэффициенты модели множественной регрессии;

– случайные ошибки модели множественной регрессии.

При построении нормальной линейной модели множественной регрессии учитываются пять условий:

1) факторные переменные x1i…xmi – неслучайные или детерминированные величины, которые не зависят от распределения случайной ошибки модели регрессии

2) математическое ожидание случайной ошибки модели регрессии равно нулю во всех наблюдениях:

3) дисперсия случайной ошибки модели регрессии постоянна для всех наблюдений:

4) между значениями случайных ошибок модели регрессии в любых двух наблюдениях отсутствует систематическая взаимосвязь, т.е. случайные ошибки модели регрессии не коррелированны между собой (ковариация случайных ошибок любых двух разных наблюдений равна нулю):

Это условие выполняется в том случае, если исходные данные не являются временными рядами;

5) на основании третьего и четвёртого условий часто добавляется пятое условие, заключающееся в том, что случайная ошибка модели регрессии – это случайная величина, подчиняющейся нормальному закону распределения с нулевым математическим ожиданием и дисперсией G2:

Общий вид нормальной линейной модели парной регрессии в матричной форме:

Y=X*

Где

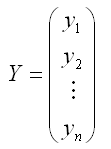
– случайный вектор-столбец значений результативной переменной размерности (n*1);

– матрица значений факторной переменной размерности (n*(m+1)). Первый столбец является единичным, потому что в модели регрессии коэффициент умножается на единицу;

– вектор-столбец неизвестных коэффициентов модели регрессии размерности ((m+1)*1);

– случайный вектор-столбец ошибок модели регрессии размерности (n*1).

Включение в линейную модель множественной регрессии случайного вектора-столбца ошибок модели обусловлено тем, что практически невозможно оценить связь между переменными со 100-процентной точностью.

Условия построения нормальной линейной модели множественной регрессии, записанные в матричной форме:

1) факторные переменные x1j…xmj – неслучайные или детерминированные величины, которые не зависят от распределения случайной ошибки модели регрессии. В терминах матричной записи Х называется детерминированной матрицей ранга (k+1), т.е. столбцы матрицы X линейно независимы между собой и ранг матрицы Х равен m+1<n;< em=""></n;<>

2) математическое ожидание случайной ошибки модели регрессии равно нулю во всех наблюдениях:

3) предположения о том, что дисперсия случайной ошибки модели регрессии является постоянной для всех наблюдений и ковариация случайных ошибок любых двух разных наблюдений равна нулю, записываются с помощью ковариационной матрицы случайных ошибок нормальной линейной модели множественной регрессии:

где

G2

In – единичная матрица размерности (n*n).

4) Х случайной величиной, подчиняющейся многомерному нормальному закону распределения с нулевым математическим ожиданием и дисперсией G2:

В нормальную линейную модель множественной регрессии должны входить факторные переменные, удовлетворяющие следующим условиям:

1) данные переменные должны быть количественно измеримыми;

2) каждая факторная переменная должна достаточно тесно коррелировать с результативной переменной;

3) факторные переменные не должны сильно коррелировать друг с другом или находиться в строгой функциональной зависимости.