Аксіоми статики
Аксіома 1 (про рівновагу абсолютно твердого тіла під дією двох сил)
Вільне абсолютно тверде тіло знаходиться у рівновазі під дією двох сил, тоді коли сили діють по одній прямій у протилежні сторони й мають рівні модулі.

{F1,F2} ∾ 0 коли: F1=F2; лінії дії сил F1 й F2 співпадають.
Аксіома 2( про приєднання й відкидання системи сил, яка еквівалентна нулю)
Дія даної системи сил на абсолютно тверде тіло не зміниться, якщо до неї приєднати або від неї прибрати систему сил еквівалентну нулю.
{F1,F2…Fn} ∾{F1,F2…Fn, Q1,Q2...Qn}, якщо {Q1,Q2...Qn} ∾ 0.
Аксіома 3 (паралелограма сил)

Дві сили, прикладені в одній точці тіла, еквівалентні рівнодіючій, прикладеній у тій самій точці яка визначається як діагональ паралелограма, побудованого на силах, як на сторонах.
{F1, F2}∾ R якщо:
- R=F1+F2,
- Сила F1,F2,R прикладені в одній точці.
Аксіома 4 (дія й протидія)
Сили взаємодії двох тіл рівні за величиною й спрямовані по одній прямій в протилежні сторони.
Тобто: дія тіла 1 на тіло 2 (сила F12) дорівнює й протилежно спрямована дії тіла 2 на тіло 1(сила F21)
а)F21= -F12
б) лінії дії F21 й F12 співпадають
Якщо на переміщення точок тіла накладаються обмеження, то тіло називається невільним, або зв’язаним. Матеріальні тіла, які обмежують переміщення даного тіла, називаються зв’язками.
Сила з якою зв’язок діє на дане тіло, називається реакцією зв’язків.
Зв’язки бувають внутрішніми й зовнішніми.
Внутрішнім зв’язком називається зв’язок, який накладає обмеження тільки на відносне розміщення точок розглядаємої системи. У протилежному випадку зв’язок буде зовнішнім.
(Тіла які належать даній системі - внутрішні, тіла які не належать даній системі- зовнішні). Наприклад, для залізничного вагона рельси - зовнішній зв’язок, а з’єднання візка вагона з низом-внутрішній.
Аксіома 5 (про зв’язки)
Рівновага тіла непорушиться,якщо накладені на неї зв’язки замінити реакціями зв’язків.
Наслідки з аксіом
Наслідок 1
Силу, прикладену до абсолютно твердого тіла, можна переносити у будь-яку точку її лінії дії. При цьому дія сили на тіло не змінюється.
Наслідок 2
(Теорема трьох сил, або необхідні умови рівноваги тіла, яке знаходиться під дією трьох непаралельних сил). Якщо вільне тіло знаходиться у стані рівноваги під дією трьох непаралельних сил, які лежать в одній площині, то лінії дії цих сил перетинаються в одній точці.

Тема 1.2 Плоска система збіжних сил.
Засоби визначення рівнодіючої сили.

Правило багатокутника
R=F1+F2+F3+F4
Вектор R є геометричною сумою векторів.
{F1, F2, F3, F4} ∾ R
У відношенні до силового багатокутника вектор R є його замінюючою стороною (або просто змінюючою). Вимірюючи довжину вектора R й кута  , визначаємо величину й напрямок рівнодіючої системи сил яка розглядається.
, визначаємо величину й напрямок рівнодіючої системи сил яка розглядається.
3. Аналітичний засіб знаходження рівнодіючої сили.
{F1, F2,…Fn}- система збіжних сил на площині.
На підставі теореми із п.1 ця система має рівнодіючу R, яка є геометричною сумою сил системи.
n
R= 
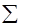 Fk
Fk
R=1
R  й R
й R  - проекції рівнодіючих на осі декартової прямокутної системи.
- проекції рівнодіючих на осі декартової прямокутної системи.
X1,Y1,X2,Y2,…XnYn- проекції сил F1,F2…Fn на ті самі осі. Тоді за теоремою про проекції суми векторів
n
Rx=X1+X2+…Xn= 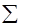 Xr
Xr
R=1
n
Ry=Y1+Y2+…+Y3= 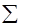 Yr
Yr
R=1
R=  =
= 
 cos
cos  =
= 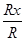 cos
cos  =
= 
 - кути, які утворюються рівнодіючою R, з координатними вісями Ox та Oy.
- кути, які утворюються рівнодіючою R, з координатними вісями Ox та Oy.






