Қыздырғыштарды жылулық есептеуде олардың термиялық кедергісін және жұмыс температурасын немесе меншікті беттік қуатын анықтайды.
Біз жалпы әдістемелік принципін және қарапайым мысалдарды қарастырамыз.
Қыздырғыштардан жылу беріліс күрделі сипатты болады. Өйткені температуралық өріс күрделі келеді және бір құрылғыдан жылу беріліс жылу өткізгіштікпен, конвекциямен және сәулеленумен болады.
1.1. Жылу өткізгіштікпен жылу беріліс. Қыздырғыш қыздырылатын материалмен тікелей түйісіп тұрса немесе олардың арасындағы орта инфрақызыл сәулелерін өткізбейтін болса қыздырғыштан жылу беріліс жылу өткізгіштікпен жүзеге асырылады. Осы жылу беріліс тәсілінде берілетін қуат Фурье заңымен анықталады. Қыздырғыш шексіз өлшемді пластина түрінде орындалған және қалыңдығы  бірқалыпты қабатпен қоршалған болатын идеал жағдайда Фурье заңы былай жазылады [1,2,3,4]:
бірқалыпты қабатпен қоршалған болатын идеал жағдайда Фурье заңы былай жазылады [1,2,3,4]:
 , (1)
, (1)
мұндағы  – қыздырылатын материалдың жылу өткізгіштік коэффициенті,
– қыздырылатын материалдың жылу өткізгіштік коэффициенті,  ;
;
 – қыздырғыштың температурасы,
– қыздырғыштың температурасы,  ;
;
 – қыздырылатын материалдың сыртқы бетінің температурасы,
– қыздырылатын материалдың сыртқы бетінің температурасы,  ;
;
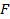 – жылу беріліс бетінің (қыздырғыштың актив бетінің) ауданы,
– жылу беріліс бетінің (қыздырғыштың актив бетінің) ауданы, 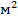 .
.
Меншікті беттік қуат ( ) [1,2,3,4]:
) [1,2,3,4]:
 , (2)
, (2)
Мынадай белгілер енгіземіз:
 – қыздырғыштан қыздырылатын ортаға бағытталған температуралық арын,
– қыздырғыштан қыздырылатын ортаға бағытталған температуралық арын,  ;
;
 – қалыңдығы
– қалыңдығы  бір қабат жазық қабырғаның
бір қабат жазық қабырғаның  -ның термиялық кедергісі,
-ның термиялық кедергісі,  ;
;
Сонда:
 , (2 а)
, (2 а)
Қабырғаның толық термиялық кедергісі  және меншікті беттік қуаты
және меншікті беттік қуаты  белгілі болғанда қыздырғыштың температурасын
белгілі болғанда қыздырғыштың температурасын  , анықтауға болады [1,2,3,4]:
, анықтауға болады [1,2,3,4]:
 , сонда
, сонда  ,
,
немесе температура  және термиялық кедергі
және термиялық кедергі  белгілі болғанда, қыздырғыштың актив бетін анықтауға болады:
белгілі болғанда, қыздырғыштың актив бетін анықтауға болады:
 , сонда
, сонда  , (3)
, (3)
Нақты қыздырғыш қондырғыларда термиялық кедергі күрделі тәуелділікпен анықталады. Термиялық кедергі мына параметрлерге тәуелді анықталады:
1) қыздырғыш кедергілердің пішініне;
2) қыздырғыш кедергілердің геометриялық өлшемдеріне;
3) электрлік оқшауламасына;
4) қыздырылатын материалдың біртектілігіне.
Қыздырғыштардың құрастырымдылық орындалуына сәйкес термиялық кедергіні анықтауға арналған формулалар арнайы әдебиеттерде беріледі.
Қыздырғыштар көп қабатты центрлес цилиндрлер түрінде дайындалады. Мысалы, түтікті электр қыздырғыштар (1-сурет).
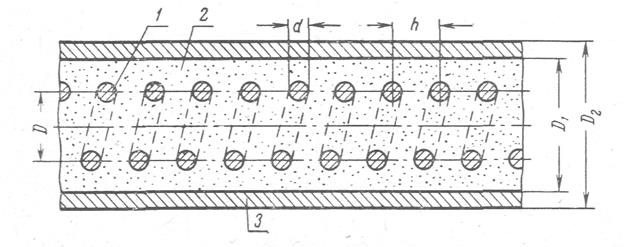
1-сурет. Түтікті электр қыздырғыштың құрылысы:
1-спираль; 2-толтырғыш; 3-түтік
Металл түтіктің (3) ішінде түтіктен толтырғышпен (2) оқшауланған нихром спираль (1) орналасқан.
Қыздырғыштың  ұзындығына есептегенде, спиральмен түтікке бағытталған жылу ағынына толтырғыштың келтіретін термиялық кедергісі мына тәуелділікпен (жартылай эмперикалық) анықталады [1,2,3,4]:
ұзындығына есептегенде, спиральмен түтікке бағытталған жылу ағынына толтырғыштың келтіретін термиялық кедергісі мына тәуелділікпен (жартылай эмперикалық) анықталады [1,2,3,4]:
 , (4)
, (4)
мұндағы λ1 – толтырғыштың жылу өткізгіштік коэффициенті, Вт/м · 0С;
D – спилальдің орташа диаметрі, м;
h – спираль орамасының адымы, м;
Ұзындығы 1м сыртқы бір қабатты цилиндр қабырғаның термиялық кедергісі [1,2,3,4]:
 , (5)
, (5)
мұндағы D1 және D2 – цилиндр қабырғаның ішкі және сыртқы диаметрлері, м;
λ2 – қабырға материалының жылу өткізгіштік коэффициенті, Вт/м · 0С;
Спиральден қыздырғыштың сыртқы бетіне бағытталған жылу ағынына толтырғыш пен түтік қабырғасының көрсететін қосынды термиялық кедергісі [1,2,3,4]:

 , (6)
, (6)
Қыздырғыштың 1м ұзындығынан алынатын қуат (Вт/м) [1,2,3,4]:
 , (7)
, (7)
мұндағы ∆t – спираль мен түтіктің сыртқы бетінің температураларының айырымы, 0С.
Спираль сымының меншікті беттік қуатын анықтау үшін былай істейміз. Сымның беті диаметрі DЭ эквиваленттік цилиндрдің бетіне тең. Бұл цилиндрге ұзындығы 1м толтырғыштың термиялық кедергісі
 , (8)
, (8)
Түрлендірулер орындаймыз:
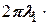
 ;
;  ;
;
 ,
,
Немесе
 , (9)
, (9)
Меншікті термиялық кедергі (сым бетінің 1м2-нен жылу ағынына)
 , (10)
, (10)
ал меншікті беттік қуат
 , (11)
, (11)
МЫСАЛ
Түтікті электр қыздырғыштың (ТЭҚ) спиралінен қыздырғыштың сыртқы бетіне бағытталған жылу ағынына көрсетілетін термиялық кедергіні анықтау керек (1-сурет). ТЭҚ-тың параметрлері: d=0,5 мм, D=5 мм, h = 2 мм, D1 = 10 мм, D2 = 13 мм. Толтырғыштың жылу өткізгіштік коэффициенті λ1 = 1,5 Вт/(м· оС), сыртқы түтігінің жылу өткізгіштік коэффициенті λ2 = 40 Вт/(м · оС).
Ұзындығы 1 м толтырғыштың термиялық кедергісін (4) өрнек бойынша анықтаймыз:

мұндағы  ;
;  ;
;  ;
;
Ұзындығы 1 м түтіктің термиялық кедергісіне (5) өрнек бойынша анықтаймыз:
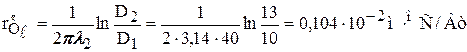
Жылу –өткізгіштіктің жалпы термиялық кедергісін (6) өрнек бойынша анықтаймыз:

(9) өрнек бойынша баламалық (эквиваленттік) цилиндрдің диаметрін анықтаймыз:
 .
.
(10) өрнек бойынша меншікті термиялық кедергіні (1 м2 – беттен тер-миялық кедергіні) анықтаймыз:

Конвективтік жылу беріліс
Конвективті жылу алмасуда қыздырғыштан қыздырылатын ортаға жылылық беріліс қыздырғыштың жанында (маңында) табиғи немесе амалсыз үзіліссіз қозғалыс жасайтын сұйықтың немесе газдың бөлшектерімен жүзеге асырылады. Қарапайым жағдайда қыздырғыштың жылу ағыны Ньютон формуласымен анықталады:
 , (12)
, (12)
мұндағы α – қыздырғыш бетінен газ немесе сұйық ортаға жылу бергіштік коэффициеті, Вт/м2 · 0С;
Жылу бергіштік коэффициенті көптеген себепкер шарттарға тәуелді келеді, олардың ішіндегі негізгілері:
1) конвекцияның түрі (табиғи немесе амалсыз)
2) қыздырғыштың температурасы;
3) қыздырғыштың пішіні;
4) қыздырғыштың геометриялық өлшемдері;
5) қоршаған сұйықтың немесе газдың жылдамдығы мен қасиеттері.
Жылу алмасудың әртүрлі жағдайларына жылу бергіштік коэффи-циентінің мәндерін негізінде тәжірибе арқылы анықтайды. Зерттеу нәти-желерін ұқсастық теория көмегімен өңдейді және критерийлер теңдеулері түрінде көрсетеді. Мысалы, газ ағынында көлденең орналасқан түтікті қыздырғыштардан жылу бергіштік мына теңдеумен көрсетіледі [1,2,3,4]:
 , (13)
, (13)
 - Нуссельт критерийі;
- Нуссельт критерийі;
 - Рейнольдс критерийі;
- Рейнольдс критерийі;
 - Прандтль критерийі,
- Прандтль критерийі,
мұндағы α – жылу бергіштік коэффициенті;
D – қыздырғыштың сыртқы диаметрі;
λ – газдың жылу өткізгіштік коэффициенті;
ω – қыздырғыштар шоғының енсіз (ең кіші) қимасындағы газ жылдамдығы;
ν– газдың кинематикалық тұтқырлығы;
a – газдың температура өткізгіштік коэффициенті;
С – тұрақты; n және m – дәрежелер көрсеткіштері.
Көлденең газ ағынында шахмат тәртібімен орналасқан тегіс түтікті қыздырғыштарға, жоғарыда келтірілген (13) өрнек негізінде, жылу бергіштік коэффициенттері мына формуламен анықталады. 
сонда  (14)
(14)
 болғанда
болғанда  , (15)
, (15)
 , (16)
, (16)
мұндағы  – қыздырғыштардың диаго-наль адымы (2, а -сурет); С – бойлық бағыттағы қыздырғыштар қатарының санына түзету коэффициенті (2, б-сурет).
– қыздырғыштардың диаго-наль адымы (2, а -сурет); С – бойлық бағыттағы қыздырғыштар қатарының санына түзету коэффициенті (2, б-сурет).
 С – түзету коэффициенті
С – түзету коэффициенті
Z- қатарлар саны
2-сурет. Ауа ағыны көлденең бағытталғанда түтікті электр
қыздырғштан жылу берілісті есептеуге:
а – қыздырғыштардың орналасу сұлбасы;
б – бойлық қатарлар санына түзету коэффициенті
Конвективтік жылу алмасуда меншікті беттік қуат, Вт/м2:
 , (17)
, (17)
∆t=t-t0; rT=1/α - түйіспелік кедергі деп аталатын, қабырға – сұйық немесе қабырға – газ шекарасындағы конвекцияның термиялық кедергісі, м2 · оС/Вт.
Конвективтік жылу алмасуда қыздырғыштың актив бетінң ауданы, м2, былай анықталады:
 , (18)
, (18)
Цилиндр пішінді денелерге конвекцияның ұзындық термиялық кедергісі, (м· оС/Вт):
 , (19)
, (19)
 Түтікті қыздырғыштардың спиральдеріне толық ұзындық термиялық кедергі жылу өткізгіштіктің және конвекцияның термиялық кедергілерінің қосындысы ретінде анықталады (м · оС/Вт):
Түтікті қыздырғыштардың спиральдеріне толық ұзындық термиялық кедергі жылу өткізгіштіктің және конвекцияның термиялық кедергілерінің қосындысы ретінде анықталады (м · оС/Вт):
 , (20)
, (20)
ал меншікті термиялық кедергі (м2 · оС/Вт):

 (21)
(21)
Меншікті беттік қуат (Вт/м2):
 , (22)
, (22)
мұндағы ∆t – спираль мен қыздырылатын орта температураларының айырымы.
Ауа еркін айналып ағатын ашық сым спиральге жылу бергіштікті мына формула бойынша есептеуге болады:
 , (23)
, (23)
Түрлендірулер орындағанда
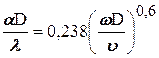 ;
;  , (24)
, (24)
 ; сонда
; сонда  , (25)
, (25)
МЫСАЛ
Ауа ағыны тегіс түтікті қыздырғышты көлденең бағытта айналып аққан жағдайда қыздырғыш спиралінің температурасын және меншікті беттік қуатын анықтау керек (1-сурет). Ауа ағынның жылдамдығы ω=10м/с, ауаның орташа температурасы t0=30оС. Түтікті электр қыздырғыштың (ТЭҚ) сыртқы бетінің температурасы t2=400оС. Қыздырғыштар шахмат ретімен (тәртібімен) орналастырылған. Қыздырғыштар шоғының параметрлері (2-сурет): D = D2 = 13 мм, S1 = 26 мм, S2 = 13 мм, ауа ағынының бағыты бойынша қыздырғыштар қатарының саны Z = 5.
Қыздырғыштар шоғының диогональдық адымын анықтаймыз:
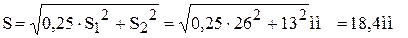
Өлшемсіз параметрді анықтаймыз:

(14) өрнек бойынша жылу бергіштік коэффициентін «α» анықтаймыз. Қажетті параметрлер:
Температура t0=30оС болғанда ауаның физикалық сипаттамалары: жылу өткізгіштік коэффициенті λ=2,58·10-2 Вт/(м· оС), кинематикалық тұт-қырлығы ν =1,66· 10-5 м2/С, Прандтль критерийі Рr=0,702. 2,б-суретте келтірілген график бойынша Z = 5 болғанда, түзететін коэффициенттің мәні С = 0,9.
Сонда (14) өрнек бойынша

Қыздырғыштың меншікті түйіспелік термиялық кедергісін анықтай-мыз:

Ұзындығы 1 м қыздырғыштың түйіспелік кедергісін анықтаймыз:

Ұзындығы 1 м қыздырғыштың жалпы термиялық кедергісін анық-таймыз:


мұндағы  - ұзындығы 1 м толтырғыштың термиялық кедергісі, 1-мысалдан алынды.
- ұзындығы 1 м толтырғыштың термиялық кедергісі, 1-мысалдан алынды.
(17) өрнек бойынша жалпы меншікті термиялық кедергіні анық-таймыз:
 ,
,
мұндағы Dэ = 3,5 мм баламалық цилиндрдің диаметрі, 1-мысалдан алынды.
Қыздырғыштың сыртқы бетіндегі меншікті қуатты анықтаймыз:

Ұзындығы 1 м қыздырғыштың меншікті қуатын анықтаймыз:

Спиральдің температурасын анықтаймыз:

Спиральдің температурасын мына формуламен де есептеуге болады
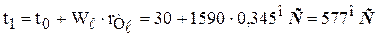
Спиральдің меншікті беттік қуатын анықтаймыз:
 ,
,
 мұндағы: rТ=0,123·10-2 м2· оС/Вт – жылу өткізгіштіктің термиялық кедер-гісін, 1-мысалдан алынды.
мұндағы: rТ=0,123·10-2 м2· оС/Вт – жылу өткізгіштіктің термиялық кедер-гісін, 1-мысалдан алынды.






