Пусть задача ЛП задана в стандартной форме. Геометрически ОДР образуется пересечением m множеств, каждое из них определяется неравенством: ai1x1+ai2x2+...+ainxn≥bi и представляет собой полупространство, лежащее по одну сторону от гиперплоскости ai1x1+ai2x2+...+ainxn=bi
Пересечение полупространств является областью допустимых решений (и чаще всего выпуклым многогранником, если область ограничена и не пуста).
Линии уровня c1x1+c2x2+...+cnxn=const образуют семейство параллельных гиперплоскостей.
Вектор нормали к этим плоскостям c={c1, c2,…,cn}T перпендикулярен этим параллельным плоскостям и определяет направление возрастания линейной формы.
 |  | ||||
 | |||||
Задача Задача имеет Задача имеет Задача
неразрешима единственное решение множество решений неограничена
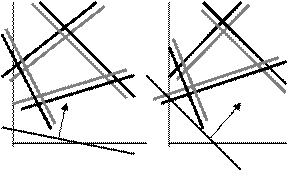
Рис.4.1. Иллюстрация существования решений задачи ЛП.
Множество точек, заданных неравенствами, может быть пустым, ограниченным и неограниченным (соответственно, задача ЛП может не иметь решения, иметь одно решение, иметь бесконечное множество решений или быть неограниченной). На рис.4.1 показаны эти случаи для задачи с двумя переменными; сплошные линии соответствуют ограничениям, серым цветом показаны полуплоскости, удовлетворяющие ограничениям; линии со стрелками соответствуют нормали к линии функции цели.
Следует иметь в виду, что оптимум задачи ЛП достигается только в ограниченной точке допустимого множества. В отличии от задач нелинейного программирования в задаче ЛП оптимум всегда является глобальным.
Графическое решение задачи линейного программирования:
Геометрический метод применяется для решения задачи ЛП двух переменных, т. к. только в этом случае можно построить наглядно ОДР на плоскости. Метод состоит из двух этапов. На первом строится ОДР как пересечение полуплоскостей, каждая из которых задана неравенством – ограничением. После второго строится прямая c1x1+c2x2=a, где a -произвольное число. Мысленно сдвигаем эту прямую параллельно самой себе вправо – вверх, если мы максимизируем целевую функцию и влево – вниз, если минимизируем. Движение продолжается до тех пор, пока прямая ещё будет принадлежать ОДР. Точное решение получаем из решения системы двух уравнений, задающих соответствующие прямые, пересечение которых даёт решение на графике. Пример: решить графически задачу ЛП:
f=x1+x2→max
-3x1+2x2≤6
x1+2x2≥2
0≤x1≤3, x2≥0
x2
 |
А
3
2
-2 -1 0 1 2 3 x1
Для графического решения задачи построим по двум точкам прямые 2x2-3x1=6; x1+2x2=2; x1=3. После этого штрихуем те полуплоскости, которые удовлетворяют неравенствам (на рис. серыми линиями)и строим ОДР как пересечение заштрихованных полуплоскостей. Затем рисуем линию уровня x1+x2=2 (вместо цифры 2 можно было подставить любую).
Так как задача ставится на максимум целевой функции, мысленно сдвигаем прямую, соответствующую целевой функции, вверх-вправо, пока она еще будет принадлежать области, ограниченной серыми линиями. Очевидно, решение находится в точке А. Для нахождения точного решения нужно решить систему из двух уравнений:
3x1+2x1=6
x1=3
Точное решение: x1=3; x2=7,5
Задания к лабораторным работам по теме "Линейное программирование"
Решить графическим методом следующие задачи линейного программирования:
1. f=x1+x2®max 2. f=x1-2x2®min
-3x1+2x2£6 x1-x2£1
x1+2x2³2 x1+x2³2
0£x1£3 x1-2x2£2
x2³0 x1³0; x2³0
3. f=x1+2x2®min 4. f=6x1+7x2®max
x1³2 x1-1³0
x1+3x2£3 x2-1³0
x1-x2+1£0 x1+x2-3³0
-6x1-7x2+42³0
5. f=3x1+2x2®max 6. f=x1+2x2®max
x1+x2£1 x1-x2£1
3x1+4x2£12 x1-2x2£1
x1³0; x2³0 x1³0; x2³0
7. f=4x1+5x2®max 8. f=x1+x2®min
2x1+3x2£6 5x1-2x2£4
-x1+x2³3 -x1+2x2£4
x1³0; x2³0 x1+x2³4
9. f=2x1+3x2®max 10. f=x1+3x2®min
8x1+5x2£11 3x1-x2³0
-x1+3x2£1 2x1-x2£6
2x1+7x2³7 x1+x2£0; x1£2
x1³0; x2³0 3x1-x2³-4
11. f=3x1+x2®min 12. f=x1+x2®max
0£x1£2 0,5£x1+x2£1
x1+x2-2³0 x1-2x2£1
x1-x2+1£0 3x1+2x2£3
x1³0; x2³0
13. f=x1+x2®max 14. f=2x1+x2®min
x1+x2-5³0 2x1-x2³-2
x1-x2-5³0 x1-x2³-2
x1£7 x1£1; 2x1-x2³3
