Сущность и значение моделирования, требования к нему. Основные типы факторных детерминированных моделей. Способы преобразования факторных моделей. Правила моделирования.
Одной из задач факторного анализа является моделирование взаимосвязей между результативными показателями и факторами, которые определяют их величину.
Моделирование - это один из важнейших методов научного познания, с помощью которого создается модель (условный образ) объекта исследования. Сущность его заключается в том, что взаимосвязь исследуемого показателя с факторными передается в форме конкретного математического уравнения.
В факторном анализе различают модели детерминированные (функциональные) и стохастические (корреляционные). С помощью детерминированных факторных моделей исследуется функциональная связь между результативным показателем (функцией) и факторами (аргументами).
При моделировании детерминированных факторных систем необходимо выполнять ряд требований.
1. Факторы, включаемые в модель, и сами модели должны иметь определенно выраженный характер, реально существовать, а не быть придуманными абстрактными величинами или явлениями.
2. Факторы, которые входят в систему, должны быть не только необходимыми элементами формулы, но и находиться в причинно-следственной связи с изучаемыми показателями. Иначе говоря, построенная факторная система должна иметь познавательную ценность. Факторные модели, которые отражают причинно-следственные отношения между показателями, имеют значительно большее познавательное значение, чем модели, созданные при помощи приемов математической абстракции. Последнее можно проиллюстрировать следующим образом. Возьмем две модели:
1)ВП=ЧР х ГВ:
2)ГВ=ВП/ЧР, где ВП - валовая продукция предприятия; ЧР - численность работников на предприятии; ГВ — среднегодовая выработка продукции одним работником.
В первой системе факторы находятся в причинной связи с результативным показателем, а во второй — в математическом соотношении. Значит, вторая модель, построенная на математических зависимостях, имеет меньшее познавательное значение, чем первая.
3. Все показатели факторной модели должны быть количественно измеримыми, т.е. должны иметь единицу измерения и необходимую информационную обеспеченность.
4. Факторная модель должна обеспечивать возможность измерения влияния отдельных факторов, это значит, что в ней должна учитываться соразмерность изменений результативного и факторных показателей, а сумма влияния отдельных факторов должна равняться общему приросту результативного показателя.
В детерминированном анализе выделяют следующие типы наиболее часто встречающихся факторных моделей.
1. Аддитивные модели:

Они используются в тех случаях, когда результативный показатель представляет собой алгебраическую сумму нескольких факторных показателей.
2. Мультипликативные модели:

Этот тип моделей применяется тогда, когда результативный показатель представляет собой произведение нескольких факторов.
3. Кратные модели:

Они применяются тогда, когда результативный показатель получают делением одного факторного показателя на величину другого.
4. Смешанные (комбинированные) модели - это сочетание в различных комбинациях предыдущих моделей:
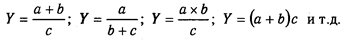
Моделирование мультипликативных факторных систем в АХД осуществляется путем последовательного расчленения факторов исходной системы на факторы-сомножители. Например, при исследовании процесса формирования объема производства продукции (см. рис. 5.2) можно применять такие детерминированные модели, как:

Эти модели отражают процесс детализации исходной факторной системы мультипликативного вида и расширения ее за счет расчленения на сомножители комплексных факторов. Степень детализации и расширения модели зависит от цели исследования, а также от возможностей детализации и формализации показателей в пределах установленных правил.
Аналогичным образом осуществляется моделирование аддитивных факторных систем за счет расчленения одного или нескольких факторных показателей на составные элементы.
Как известно, объем реализации продукции равен:
VРП = VBП - VИ,
где VBП - объем производства; VИ - объем внутрихозяйственного использования продукции.
В хозяйстве продукция использовалась в качестве семян (С) и кормов (К). Тогда приведенную исходную модель можно записать следующим образом: VРП = VBП - (С + К).
К классу кратных моделей применяют следующие способы их преобразования: удлинения, формального разложения, расширения и сокращения.
Первый метод предусматривает удлинение числителя исходной модели путем замены одного или нескольких факторов на сумму однородных показателей. Например, себестоимость единицы продукции можно представить в качестве функции двух факторов: изменения суммы затрат (3) и объема выпуска продукции (VBП). Исходная модель этой факторной системы будет иметь вид

Если общую сумму затрат (3) заменить отдельными их элементами, такими, как заработная плата (3П), сырье и материалы (СМ), амортизация основных средств (А), накладные расходы (HP) и др., то детерминированная факторная модель будет иметь вид аддитивной модели с новым набором факторов:

где Х1 — трудоемкость продукции; Х2 - материалоемкость продукции; Х3 - фондоемкость продукции; Х4 - уровень накладных расходов.
Способ формального разложения факторной системы предусматривает удлинение знаменателя исходной факторной модели путем замены одного или нескольких факторов на сумму или произведение однородных показателей. Если В = L+М+N+Р,то

В результате, получили конечную модель того же вида, что и исходной факторной системы (кратную модель). На практике такое разложение встречается довольно часто. Например, при анализе показателя рентабельности производства (R):
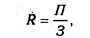
где П — сумма прибыли от реализации продукции; 3 — сумма затрат на производство и реализацию продукции. Если сумму затрат заменить на отдельные ее элементы, конечная модель в результате преобразования приобретет следующий вид:

Себестоимость одного тонно-километра зависит от суммы затрат на содержание и эксплуатацию автомобиля (3) и от его среднегодовой выработки (ГВ). Исходная модель этой системы будет иметь вид: С ткм = 3 / ГВ. Учитывая, что среднегодовая выработка машины в свою очередь зависит от количества отработанных дней одним автомобилем за год (Д), продолжительности смены (П) и среднечасовой выработки (ЧВ), мы можем значительно удлинить эту модель и разложить прирост себестоимости на большее количество факторов:

Метод расширения предусматривает расширение исходной факторной модели за счет умножения числителя и знаменателя дроби на один или несколько новых показателей. Например, если в исходную модель
Y=A/B
ввести новый показательс, то модель примет вид

В результате получилась конечная мультипликативная модель в виде произведения нового набора факторов.
Этот способ моделирования очень широко применяется в анализе. Например, среднегодовую выработку продукции одним работником (показатель производительности труда) можно записать таким образом: ГВ = ВП /ЧР. Если ввести такой показатель, как количество отработанных дней всеми работниками (D), то получим следующую модель годовой выработки:

где ДВ — среднедневная выработка; Д - количество отработанных дней одним работником.
После введения показателя количества отработанных часов всеми работниками (Г) получим модель с новым набором факторов: среднечасовой выработки (ЧВ), количества отработанных дней одним работником (Д) и продолжительности рабочего дня (Я):

Способ сокращения представляет собой создание новой факторной модели путем деления числителя и знаменателя дроби на один и тот же показатель:
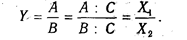
В данном случае получается конечная модель того же типа, что и исходная, однако с другим набором факторов.
И снова практический пример. Как известно, экономическая рентабельность работы предприятия рассчитывается делением суммы прибыли (П) на среднегодовую стоимость основного и оборотного капитала предприятия (KL):
R = П / KL.
Если числитель и знаменатель разделим на объем реализации продукции (товарооборот), то получим кратную модель, но с новым набором факторов: рентабельности продаж и капиталоемкости продукции:

И еще один пример. Фондоотдача (ФО) определяется отношением валовой (ВП) или товарной продукции (ТП) к среднегодовой стоимости основных производственных фондов (ОПФ):
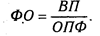
Разделив числитель и знаменатель на среднегодовое количество рабочих (ЧР), получим более содержательную кратную модель с другими факторными показателями: среднегодовой выработки продукции одним рабочим (ГВ), характеризующей уровень производительности труда, и фондовооруженности труда (Фв):

Необходимо заметить, что на практике для преобразования одной и той же модели может быть последовательно использовано несколько методов. Например:
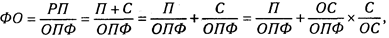
где ФО - фондоотдача; РП - объем реализованной продукции (выручка); С - себестоимость реализованной продукции; П - прибыль; ОПФ —среднегодовая стоимость основных производственных фондов; ОС — средние остатки оборотных средств.
В этом случае для преобразования исходной факторной модели, которая построена на математических зависимостях, использованы способы удлинения и расширения. В результате получилась более содержательная модель, которая имеет большую познавательную ценность, так как учитывает причинно-следственные связи между показателями. Полученная конечная модель позволяет исследовать, как влияют на фондоотдачу рентабельность основных средств производства, соотношения между основными и оборотными средствами, а также коэффициент оборачиваемости оборотных средств.
Таким образом, результативные показатели могут быть разложены на составные элементы (факторы) различными способами и представлены в виде различных типов детерминированных моделей. Выбор способа моделирования зависит от объекта исследования, поставленной цели, а также от профессиональных знаний и навыков исследователя.
Процесс моделирования факторных систем - очень сложный и ответственный момент в АХД. От того, насколько реально и точно созданные модели отражают связь между исследуемыми показателями, зависят конечные результаты анализа.






