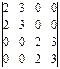 анықтауышының мәні жататын аралық: D) (-3; 2).F) (-2; 2).
анықтауышының мәні жататын аралық: D) (-3; 2).F) (-2; 2).
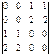 анықтауышының мәні жататын аралық: D) (-4; 2).F) (-4; 4).
анықтауышының мәні жататын аралық: D) (-4; 2).F) (-4; 4).
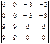 анықтауышының мәні жататын аралық: А) (-3; 3).F) (-6; 6).
анықтауышының мәні жататын аралық: А) (-3; 3).F) (-6; 6).
Диагоналдық матрица: E) 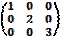 .
.
Матрицаны элементар түрлендіру дегеніміз: A) матрицаның екі жолын ауыстыру.B) матрицаның бір жолы мен бір бағанын ауыстыру.F) матрицаның бір жолын бір санға қосып, басқа жолға көбейту.
n – ші ретті анықтауыштың бүйір диоганаль бойындағы элементтердің көбейтіндісі мынадай таңбамен анықталады: A) Теріс таңбамен.F) 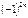 таңбамен.
таңбамен.
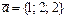 және
және 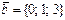 векторларының скаляр көбейтіндісінің мәні қай аралыққа тиісті: E)
векторларының скаляр көбейтіндісінің мәні қай аралыққа тиісті: E) 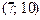 .
.
Егер  ,
, 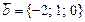 болса, онда: B)
болса, онда: B) 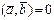 .D)
.D) 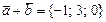 .H) ортогональ векторлар.
.H) ортогональ векторлар.
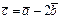 векторының ұзындығы қай аралыққа тиісті, егер
векторының ұзындығы қай аралыққа тиісті, егер 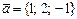 және
және 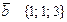 векторлары берілсе:. C)
векторлары берілсе:. C) 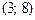 .D)
.D) 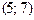 .
.
Ортогональ болатын векторлар жұбы: A) 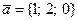 және
және 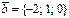 .E)
.E) 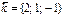 және
және 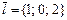 .
.
Ортогональ болатын векторлар жұбы: B) 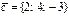 және
және 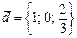 .
.
Коллинеар болатын векторлар жұбы: C) 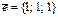 және
және 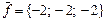 .E)
.E) 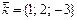 және
және 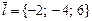 .
.
Коллинеар болатын векторлар жұбы H) 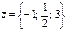 және
және 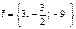 .
.
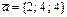 және
және 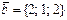 векторларының арасындағы бұрыштың косинусының мәні мына аралыққа тиісті: B)
векторларының арасындағы бұрыштың косинусының мәні мына аралыққа тиісті: B) 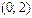 .
.
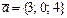 және
және 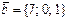 векторларының арасындағы бұрышы: C)
векторларының арасындағы бұрышы: C) 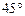 .D)
.D) 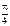 .
.
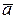 және
және 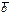 векторларының векторлық көбейтіндісінен шығатын вектор.........: A) осы векторлардың ұзындықтарымен олардың арасындағы бұрыштың синусының көбейтіндісіне тең.D)
векторларының векторлық көбейтіндісінен шығатын вектор.........: A) осы векторлардың ұзындықтарымен олардың арасындағы бұрыштың синусының көбейтіндісіне тең.D) 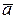 және
және 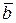 векторларының әрқайсысына перпендикуляр.F) бағыты «оң қол ережесіне» сәйкес.
векторларының әрқайсысына перпендикуляр.F) бағыты «оң қол ережесіне» сәйкес.
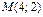 нүктесі
нүктесі 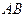 кесіндісің ортасы болады, егер
кесіндісің ортасы болады, егер 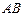 кесіндісінің нүктелері мына түрде болса: B)
кесіндісінің нүктелері мына түрде болса: B) 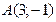 ,
, 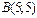 .
.
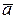 ,
, 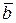 ,
, 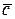 векторлары компланар дейміз, егер: A)
векторлары компланар дейміз, егер: A) 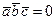 .F) олар параллель болатын жазықтық табылады.
.F) олар параллель болатын жазықтық табылады.
Бірлік вектор дегеніміз: B) 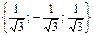 .E)
.E) 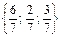 .G)
.G) 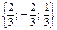 .
.
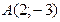 және
және 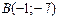 нүктелерінің арақашықтығы мына санға бөлгіш болады: A) 15.
нүктелерінің арақашықтығы мына санға бөлгіш болады: A) 15.
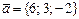 векторының ұзындығы қай аралыққа тиісті: B)
векторының ұзындығы қай аралыққа тиісті: B)  .D)
.D) 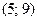 .E)
.E) 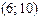 .
.
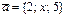 және
және 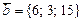 векторлары коллинеар болса,
векторлары коллинеар болса, 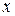 - тің мәні қай аралыққа тиісті: A)
- тің мәні қай аралыққа тиісті: A) 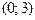 .B)
.B) 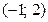 .H)
.H) 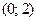 .
.
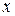 -тің қандай мәнінде
-тің қандай мәнінде 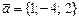 және
және 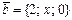 векторлары ортогональ болады: C) 0,5.F)
векторлары ортогональ болады: C) 0,5.F) 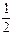 .
.
Егер 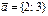 ,
, 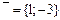 ,
, 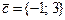 векторлары берілсе,
векторлары берілсе, 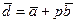 және
және 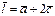 векторлары коллинеар болғанда,
векторлары коллинеар болғанда, 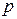 коэффициентінің мәні мына аралықта жатады: F)
коэффициентінің мәні мына аралықта жатады: F) 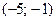 .
. 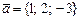
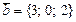
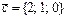 векторлары арқылы салынған параллелепипедтің көлемі мына санның бөлгіші болады: B) 54.D) 33.E) 48.
векторлары арқылы салынған параллелепипедтің көлемі мына санның бөлгіші болады: B) 54.D) 33.E) 48.
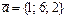 ,
, 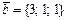 ,
, 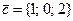 векторлары арқылы салынған тетраэдр көлемінің мәні келесі аралыққа тиісті: D)
векторлары арқылы салынған тетраэдр көлемінің мәні келесі аралыққа тиісті: D) 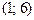 .G)
.G) 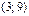 .
.
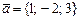 және
және 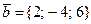 векторларының векторлық көбейтіндісі болатын
векторларының векторлық көбейтіндісі болатын 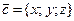 векторының координаталары мына теңдіктерді қанағаттандырады: C)
векторының координаталары мына теңдіктерді қанағаттандырады: C) 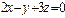 .F)
.F) 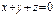 .
.
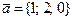 және
және 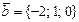 векторларының векторлық көбейтіндісі болатын
векторларының векторлық көбейтіндісі болатын 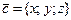 векторының координаталары мына теңдіктерді қанағаттандырады: B)
векторының координаталары мына теңдіктерді қанағаттандырады: B) 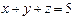 .F)
.F) 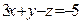 .
.
Егер 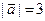 ,
, 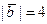 ,
, 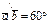 , онда
, онда 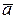 және
және 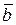 векторларының скалярлық көбейтіндісі келесі сандарға қалдықсыз бөлінеді: G) 12.H) 18.
векторларының скалярлық көбейтіндісі келесі сандарға қалдықсыз бөлінеді: G) 12.H) 18.
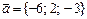 векторының орт векторы: B)
векторының орт векторы: B) 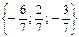 .G) ұзындығы 1-ге тең.
.G) ұзындығы 1-ге тең.
Берілгені: / 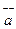 /=6,. /
/=6,. / 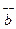 /=5,
/=5, 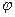 =
= 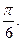
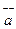 және
және 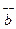 векторларының векторлық көбейтіндісінің модулі: C) 15.F)
векторларының векторлық көбейтіндісінің модулі: C) 15.F) 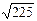 .
.
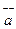 ={3,-1,-2} және
={3,-1,-2} және 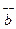 ={1,2,-1} векторларының векторлық көбейтіндісі: C) {5,1,7}.
={1,2,-1} векторларының векторлық көбейтіндісі: C) {5,1,7}.
Берілгені: 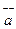 ={1,-1,3},
={1,-1,3}, 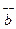 ={-2,2,1},
={-2,2,1}, 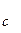 ={3,-2,5}.
={3,-2,5}. 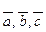
 векторларының аралас көбейтіндісі: D) -7.
векторларының аралас көбейтіндісі: D) -7.
A (3, -4) және B (-3,4) нүктелері берілген. / AB / кесіндісінің ұзындығы: B) 10.F) 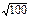
A (1,-3) және В (3,-5) нүктелері берілген. [ AB ] кесіндісінің ортасы: C) (2, -4).
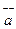 ={1,2,3} және
={1,2,3} және 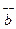 ={-2,1,2} векторларының векторлық көбейтіндісі: C) (1,-8,5).
={-2,1,2} векторларының векторлық көбейтіндісі: C) (1,-8,5).
Мына векторлар жұбы сызықтық тәуелді векторлар болады: C) 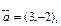
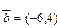 .F)
.F) 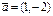 ,
, 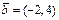 .G)
.G) 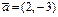 ,
, 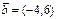 .
.
A(2,-3,4) және B(4,3,7) нүктелерінің ара қашықтығы: D) 7.F) 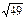 .
.
A(2,-3,5) және B(4,5,7) нүктелерінің ортасы: B) C(3,1,6).
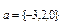 және
және 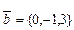 векторларының векторлық көбейтіндісі: C){6,9,3}.
векторларының векторлық көбейтіндісі: C){6,9,3}.
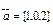
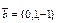 ,
, 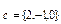 векторларының аралас көбейтіндісі: D) –5.
векторларының аралас көбейтіндісі: D) –5.






