Лабораторная работа №8. Исследование устойчивости цифровых систем
Цель работы: определение параметров замкнутой цифровой системы для обеспечения устойчивости путем математического моделирования.
Краткие сведения из теории
Передаточная функция разомкнутой импульсной системы, состоящей из идеального импульсного элемента и приведенной непрерывной части, может быть получена путем z-преобразования
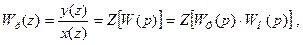
где у(z), х(z) - z-образы выходной и входной величин;
Wф(р) – передаточная функция формирующего звена;
Wн(р) - передаточная функция непрерывной части системы.
Передаточная функция замкнутой импульсной системы равна

где Woc – коэффициент передачи обратной связи.
В результате преобразований можно получить выражение
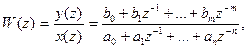
из которого следует

Переходя к оригиналу и считая, что у(z) является z-изображением ук, а х(z) - z-изображением хk, получим

Последнее выражение позволяет рассчитывать выходную величину по значениям входной величины, заданной в дискретные моменты времени.
Частотная характеристика импульсной системы определяется реакцией системы на гармоническое воздействие и получается из дискретной передаточной функции W(z) путем замены в выражении z = ехр(рТ) р на jω. Она может быть представлена аналогично частотной характеристики непрерывной системы в виде
W(jω) = A0(ω) exp(jφ(ω)),
где A0(ω) – модуль, φ(ω) – фаза частотной характеристики.
Модуль частотной характеристики равен

где Р(ω), Q(ω) – вещественная и мнимая части частотной характеристики, а ее фаза выражается соотношением

Особенностью частотных характеристик импульсных систем является их периодичность относительно частоты. Выражение z = exp(jωT) является периодической функцией частоты с периодом 2π/T. Очевидно, что для любой дискретной передаточной функции импульсной системы W(z) соответствует частотная характеристика, являющаяся периодической функцией частоты с тем же периодом.
Таким образом, для определения частотных свойств импульсной системы достаточно построить частотные характеристики на интервале ω = (0, 2π/T).
Об устойчивости разомкнутой импульсной системы можно судить по полюсам ПФ ее приведенной непрерывной части. Если приведенная непрерывная часть устойчива, то разомкнутая система будет устойчивой. Так как частотные характеристики импульсной системы аналогичны АФХ непрерывных систем, то и здесь применим критерий Найквиста:
замкнутая импульсная система устойчива, если частотная характеристика Wp (jω) устойчивой разомкнутой системы не охватывает точку (-1; j0) при изменении ω от 0 до ∞.
Чтобы замкнутая импульсная система была устойчивой при неустойчивой приведенной непрерывной части, необходимо, чтобы разность между числом положительных и отрицательных переходов частотной характеристики Wp(jω) отрезка действительной оси (-∞, -1) была равна s/2 (s – число полюсов с положительной действительной частью ПФ разомкнутой системы).
Другой метод основан на выделении областей устойчивости в плоскости комплексной величины z путем отображения линейной оси плоскости p (рис.1.а) на плоскость z. Для этой цели необходимо сделать подстановку p = jω в z-преобразование и менять частоту от -∞ до +∞, т.е. z = exp(jωT). При изменении частоты в этих пределах в плоскости z (рис.1.б) получаем окружность единичного радиуса, ограничивающую область устойчивости. Условием устойчивости будет нахождение особых точек (полюсов) ПФ замкнутой системы W(z) внутри этой окружности. Следовательно, корни характеристического уравнения 1+Wp(z) = 0 должны быть ограничены по модулю |z|<1.
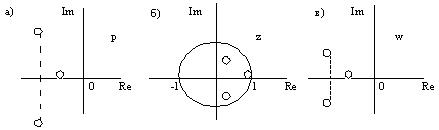
Рисунок 1 – Области устойчивости на плоскостях переменных p, z, w
Для характеристического уравнения первого порядка условие устойчивости
| a0|<1.
Для уравнения второго порядка
z2 + a1z + a0 = 0 (1)
Путем вычисления его корней получаются три условия устойчивости
1 + a1 + a0 > 0
1 - a1 + a0 > 0
a0<1 (2)
Для уравнения третьего порядка z3 + а2z2 + a1z + a0 = 0 условия устойчивости:
1 + а2 + a1 + a0 > 0
1 - а2 + a1 - a0 > 0
1 – а02 - a1 + a2а0 > 0.
Для более высокого порядка применяют w-преобразование, с помощью которого окружность единичного радиуса отображается на мнимую ось плоскости комплексной величины w. Для преобразования используется подстановка
 (3)
(3)
При подстановке z = exp(jωT) будем иметь
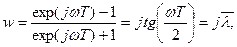
где  – относительная псевдочастота.
– относительная псевдочастота.
При малых частотах tg(ωT/2) ≈ ωT/2 и абсолютная псевдочастота λ = (2/Т) ∙ (ωT/2) = ω. При изменении частоты ω в пределах от -π/Т до π/Т псевдочастота изменяется от -∞ до ∞, а комплексная величина w движется по мнимой оси - j∞ до + j∞. Областью устойчивости в этом случае оказывается вся левая полуплоскость (рис.1,в). Поэтому для ПФ с w-преобразованием могут использоваться те же критерии устойчивости, что и для непрерывных систем.
Рассмотрим характеристическое уравнение второго порядка (1). С помощью подстановки выражения (3) оно преобразуется к виду
1 - a1 + a0) w2 + 2 (1- а0) w + 1 + a1 + a0 = 0. (4)
Применив условие критерия Гурвица (положительность коэффициентов), получаем формулу (2), получившую название критерия Шура-Кона. Использование w-преобразования дает возможность построить в функции псевдочастоты λ ЛАХ и ЛФХ для цифровых систем, аналогичные логарифмическим характеристикам непрерывных систем.
Задание
Дана следящая цифровая система, структурная схема которой имеет вид

Рисунок 2 - Структурная схема следящей цифровой системы
На рисунке 2 представлена исходная цифровая замкнутая САУ без квантования по уровню, где WНЧ – ПФ непрерывной части. ПФ приведенной непрерывной части WПНЧ получается путем перемножения ПФ непрерывной части и знаменателя ПФ АИМ – 1/р.
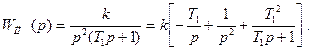
В соответствии с таблицей z-преобразования, получим ПФ приведенной непрерывной части
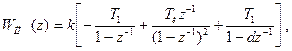
где d = ехр(-Ти /Т1).
Учитывая, что в z-преобразовании z = ехр(-рТ), тогда ПФ формирующего звена будет равна

Дискретная ПФ разомкнутой системы будет равна

После умножения на z2/z2, получим
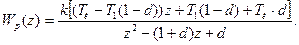
ПФ замкнутой цифровой системы равна
 (5)
(5)
Характеристическое уравнение замкнутой системы примет вид
 (6)
(6)
где 
Осуществив подстановку в формулу (6) вместо  , получим новое характеристическое уравнение в w-преобразованиях
, получим новое характеристическое уравнение в w-преобразованиях
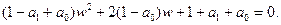
По критерию Шура-Кона для устойчивости системы коэффициенты характеристического уравнения должны быть положительными
 (7)
(7)
Подставляя в (7) а1 и а0, получим условия устойчивости



Из теории доказано, что функции kпр1 ∙ Ти и kпр2 ∙ Ти, зависящие от Ти/Т1, приблизительно равны 2. Тогда можно считать, что

Это выражение показывает, что предельный коэффициент усиления устойчивой системы обратно пропорционален длительности импульса форсирующего звена (модулятора) Ти.
Таким образом, для устойчивости следящей системы необходимо, чтобы коэффициент усиления непрерывной части находился в пределах
 (8)
(8)
Порядок выполнения работы
1). По заданным Т1 = 1с и Ти = 0,2с находим d = exp(-Ти/Т1) = 0,8187, kпр = 10 и по формуле (5) получим выражение для ПФ заданной следящей системы
 (9)
(9)
2). Изменяя k = 1, 5, 10 и внося эти значения в (9), получить ПФ и графики кривой разгона.

Рисунок 3 – Кривая разгона системы при К = 1

Р
Рисунок 4 – Кривая разгона системы при К = 5

Рисунок 5 – Кривая разгона системы при К = 10
3). Разделим (9) на z2 и получим ПФ системы
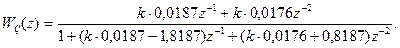 (10)
(10)
а).Составить схему по этой ПФ, используя составной блок с именем z^-1 и временем импульса Ти = 0,2с. Для создания блока z^-1 в меню Blocks-Time-unitDelay достаем блок 1/z, подсоединяем к нему на вход b блок pulse train, находящийся на панели инструментов, и выставляем к нем, в строке time between Pulses – Ти = 0,2с. Затем выделяем блоки и в меню Edit-Creat Compound Block открывается окно свойств, в котором набирается имя z^-1.

б).Плавно изменяя с помощью блока slider коэффициент k, получить кривые разгона с наилучшими показателями качества регулирования.

Рисунок 5 – Кривая разгона системы при К = 3,3
Блок Variable – задания переменных, выполняет функцию «беспроводной» связи и находится в.меню Blocks - Annotation - Variable

Курсор наводится на блок variable, нажимается пкм и в окне Set variable name записывается переменная, например, У – затем ОК. Далее берется следующий блок variable и присваивается тоже имя У, который можно перемещать в любую часть схемы.
Часто в моделях используется блок фиксации соединения wirePositioner, который позволяет удобно располагать блоки диаграммы (plot). Блок находится в меню Blocks - Annotation – wirePositioner. 
Содержание отчета
- цель работы;
- краткие сведения из теории;
- схемы и графики;
- выводы.
Контрольные вопросы
1).Чему равна ПФ замкнутой цифровой системы?
2).Чему равен выходной сигнал замкнутой цифровой системы, выраженный в разностном уравнении?
3).Действителен ли критерий Найквиста цифровых систем?
4).Что такое w-преобразование и когда оно применяется?
5).Основное достоинство и преимущество критерия Шура-Кона?
6).Что представляет собой абсолютная и относительная псевдочастота?






