In this book, three major approaches to linguistic description have been discussed till now, with different degree of detail: (1) generative approach developed by N. Chomsky, (2) the Meaning Û Text approach developed by I. Mel’čuk, and (3) constraint-based approach exemplified by the HPSG theory. In the ideal case, they produce equivalent results on identical language inputs. However, they have deep differences in the underlying ideas. In addition, they use similar terminology, but with different meaning, which may be misleading. In this section, we will compare their underlying ideas and the terminology. To make so different paradigms comparable, we will take only a bird’s-eye view of them, emphasizing the crucial commonalities and differences, but in no way pretending to a more deep description of any of these approaches just now.
Perhaps the most important commonality of the three approaches is that they can be viewed in terms of linguistic signs. All of them describe the structure of the signs of the given language. All of them are used in computational practice to find the Meaning corresponding to a given Text and vice versa. However, the way they describe the signs of language, and as a consequence the way those descriptions are used to build computer programs, is different. Generative idea. The initial motivation for the generative idea was the fact that describing the language is much more difficult, labor-consuming, and error-prone task than writing a program that uses such a description for text analysis. Thus, the formalism for description of language should be oriented to the process of describing and not to the process of practical application. Once created, such a description can be applied somehow.
Now, what is to describe a given language? In the view of generative tradition, it means, roughly speaking, to list all signs in it (in fact, this is frequently referred to as generative idea). Clearly, for a natural language it is impossible to literally list all signs in it, since their number is infinite. Thus, more strictly speaking, a generative grammar describes an algorithm that lists only the correct signs of the given language, and lists them all—in the sense that any given sign would appear in its output after a some time, perhaps long enough. The very name generative grammar is due to that it describes the process of generating all language signs, one by one at a time.
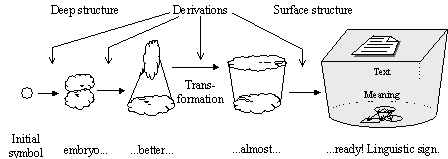FIGURE IV.16. Generative idea.
|
There can be many ways to generate language signs. The specific kind of generative grammars suggested by N. Chomsky constructs each sign gradually, through a series of intermediate, half-finished sign “embryos” of different degree of maturity (see Figure IV.16). All of them are built starting from the same “egg-cell” called initial symbol, which is not a sign of the given language. A very simple example of the rules for such gradual building is given on the pages 35 to 39; in this example, the tree structure can be roughly considered the Meaning of the corresponding string.
Where the infinity of generated signs comes from? At each step, called derivation, the generation can be continued in different ways, with any number of derivation steps. Thus, there exist an infinite number of signs with very long derivation paths, though for each specific sign its derivation process is finite.
However, all this generation process is only imaginable, and serves for the formalism of description of language. It is not—and is not intended to be—applied in practice for the generation of an infinitely long list of language expressions, which would be senseless. The use of the description—once created—for passing from Text to Meaning and vice versa is indirect. A program called parser is developed by a mathematician (not a linguist) by means of automatic “reversing” of the original description of the generative process.
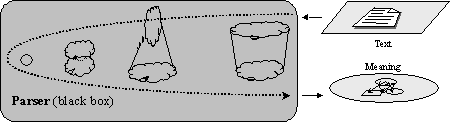FIGURE IV.17. Practical application of the generative idea.
|
This program can answer the questions: What signs would it generate that have the given Text as the signifier? What signs would it generate that have the given Meaning as signified? (See Figure IV.17.)
The parser does not really try to generate any signs, but instead solves such an equation using the data structures and algorithms quite different from the original description of the generating process.
The result produced by such a black box is, however, exactly the same: given a Text, the parser finds such Meaning that the corresponding sign belongs to the given language, i.e., would be generated by the imaginable generation algorithm. However, the description of the imaginable generation process is much clearer than the description of the internal structures automatically built by the parser for the practical applications.
Meaning Û Text idea. As any other grammar, it is aimed at the practical application in language analysis and synthesis. Unlike generative grammar, it does not concentrate on enumeration of all possible language signs, but instead on the laws of the correspondence between the Text and the Meaning in any sign of the given language. Whereas for a given text, a generative grammar can answer the question Do any signs with such Text exist, and if so, what are their Meanings?, a the MTT grammar only guarantees the answer to the question If signs with such Text existed, what would be their Meanings?
In practice, the MTT models usually can distinguish existing signs from ungrammatical ones, but mainly as a side effect. This makes the MTT models more robust in parsing.
Another idea underlying the MTT approach is that linguists are good enough at the intuitive understanding of the correspondence between Texts and Meanings, and can describe such correspondences directly. This allows avoiding the complications of generative grammars concerning the reversion of rules. Instead, the rules are applied to the corresponding data structures directly as written down by the linguist (such property of a grammar is sometimes called type transparency [47]). Direct application of the rules greatly simplifies debugging of the grammar. In addition, the direct description of the correspondence between Text and Meaning is supposed to better suite the linguistic reality and thus results in less number of rules.
Similarly to the situation with generative grammars, there can be many ways to describe the correspondence between Text and Meaning. The specific kind of the MTT grammars suggested by I. Mel’čuk describes such a correspondence gradually, through many intermediate, half-finished almost-Meanings, half-Meanings, half-Texts, and almost-Texts, as if they were located inside the same sign between its Meaning and Text (see Figure IV.18).
Since the MTT and the generative approach developed rather independently, by accident, they use similar terms in quite different and independent meanings. Below we explain the differences in the use of some terms, though these informal explanations are not strict definitions.
· In generative grammar (see Figure IV.16):
- Transformation: a term used in early works by N. Chomsky for a specific kind of non-context-free derivation.
- Deep structure, in the transformational grammar, is a half-finished sign with a special structure to which a transformation is applied to obtain a “readier” sign. It is nearer to the initial symbol than the surface structure.
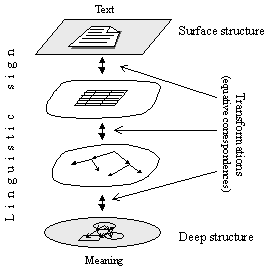FIGURE IV.18. Meaning Û Text idea.
|
- Surface structure is a half-finished sign obtained as the result of the transformation. It is nearer to the ready sign than the deep structure.
- Generation is used roughly as a synonym of derivation, to refer to the process of enumeration of the signs in the given language.
· In the MTT (see Figure IV.18):
- Transformation is sometimes used for equative correspondences between representations on different levels.
- Deep structure concerns the representation nearer to Meaning.
- Surface structure concerns the representation nearer to Text.
- Generation (of text) is used sometimes as a synonym of synthesis, i.e., construction of Text for the given Meaning.
Constraint-based idea. Similarly to the generative grammar, a constraint-based grammar describes what signs exist in the given language, however not by means of explicit listing (generation) of all such signs, but rather by stating the conditions (constraints) each sign of the given language must satisfy.
It can be viewed as if it specified what signs do not exist in the given language: if you remove one rule (generation option) from a generative grammar, it will generate less signs. If you remove one rule (constraint) from a constraint-based grammar, it will allow more signs (i.e., allow some signs that really are ungrammatical in the given language). Hence is the name constraint-based. (See also page 44.)
Since constraint-based grammars do not use the generation process shown on Figure IV.16, their rules are applied within the same sign rather than to obtain one sign from another (half-finished) one.
This makes it similar to the MTT. Indeed, though the constraint-based approach was originated in the generative tradition, modern constraint-based grammars such as HPSG show less and less similarities with Chomskian tradition and more and more similarity—not in the formalism but in meaningful linguistic structures—with the MTT.
A constraint-based grammar is like a system of equations. Let us consider a simple mathematical analogy.
Each sheet of this book is numbered at both sides. Consider the side with even numbers. Looking at the page number, say, 32, you can guess that it is printed on the 16-th sheet of the book. Let what you see be Text and what you guess be Meaning; then this page number corresponds to a “sign” <32, 16>, where we denote <T, M> a sign with the Text T and Meaning M. In order to describe such a “language”, the three approaches would use different mathematical constructions (of course, in a very rough analogy):
· Generative grammar is like a recurrent formula: The sign <2, 1> (analogue of the initial symbol) belongs to this “language”, and if < x, y > belongs to it, then < x + 2, y + 1> belongs to it (analogue of a generation rule). Note that some effort is needed to figure out from this description how to find a sheet number by a page number.
· The MTT grammar is like an algorithm: given the page number x, its sheet number is calculated as x /2; given a sheet number y, its page number is calculated as 2 ´ y. Note that we have made no attempt to describe dealing with, or excluding of, odd page numbers x, which in fact do not belong to our “language.”
· Constraint-based grammar is like an equation or system of equations. Just those signs belong to our “language,” for which x = 2 y. Note that this description is the most elegant and simple, completely and accurately describes our “language,” and requires less reversing effort for practical application than the first one. However, it is more complex than the second one.
Constraint-based idea is a very promising approach adopted by the majority of contemporaneous grammar formalisms. Probably with time, the linguistic findings of the MTT will be re-formulated in the form of constraint-based rules, possibly by a kind of merging of linguistic heritage of the MTT and formalisms developed in frame of HPSG. However, for the time being we consider the MTT more mature and thus richer in detailed description of a vast variety of linguistic phenomena. In addition, this approach is most directly applicable, i.e., it does not need any reversing.
As to the practical implementation of HPSG parsers, it is still an ongoing effort at present.
CONCLUSIONS
The definition of language has been suggested as a transformer between the two equivalent representations of information, the Text, i.e., the surface textual representation, and the Meaning, i.e., the deep semantic representation. This transformation is ambiguous in both directions: a homonymous Text corresponds to several different Meanings, and several synonymous Texts correspond to the same Meaning.
The description of the transformation process is greatly simplified by introducing intermediate levels of information representation, of which the main are morphologic and syntactic. At each level, some of the problems arising from synonymy and homonymy can be solved.
The general definitions of linguistic sign in Meaning Û Text Theory and in Head-driven Phrase Structure Grammar turned out to be in essence equivalent.
V. LINGUISTIC MODELS
THROUGHOUT THE PREVIOUS CHAPTERS, you have learned, on the one hand, that for many computer applications, detailed linguistic knowledge is necessary and, on the other hand, that natural language has a sophisticated structure, which is not easy to represent.
Thus, any application needs a description of language, i.e., the knowledge about its main properties. Such knowledge is organized in a model of language. The structure and degree of detail depend on the application’s needs.
Our objectives now are to discuss the problem of modeling in computational linguistics. We observe the modeling in general, describe shortly the neurolinguistic and psycholinguistic models, and then discuss the functional models of natural language, with a special emphasis on common features of these models.
