Лекция 5. Векторы и линейные операции над ними. Линейная зависимость и независимость векторов. Скалярное произведение векторов.
§ 5.1 Векторы: основные понятия.
В математике и ее приложениях различают два типа величин: скалярные и векторные.
Определение 5.1 Скалярной величиной или скаляром называется величина, которая полностью определяется одним числом, выражающим отношение этой величины к соответствующей единице измерения, например, масса тела, объем и др.
Другие величины, такие как скорость, ускорение, представляют собой величины, задание которых имеет смысл только тогда, когда кроме их численных значений указывается и их направление в пространстве. Такие величины называются векторными.
Определение 5.2 Направленный отрезок или упорядоченная пара точек, называется вектором.
Основные понятия:
Вектор с началом А и концом В будем обозначать  . Часто вектор обозначается одной буквой
. Часто вектор обозначается одной буквой  ,
,  и т.д. Если отрезок АВ соответствует вектору
и т.д. Если отрезок АВ соответствует вектору  , то будем писать
, то будем писать  =
=  .
.
Вектор  называется противоположным вектору
называется противоположным вектору  и обозначается
и обозначается 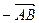 .
.
Если точки А и В совпадают, то вектор  называется нулевым, а при несовпадении этих точек – ненулевым.
называется нулевым, а при несовпадении этих точек – ненулевым.
Длиной  вектора
вектора  или его модулем называется длина
или его модулем называется длина  соответствующего направленного отрезка. Вектор, длина которого равна единице, называется единичным или ортом.
соответствующего направленного отрезка. Вектор, длина которого равна единице, называется единичным или ортом.
Вектор  =
=  называется параллельным прямой l (плоскости P), если либо он нулевой, либо прямая, проходящая через точки A и B, параллельна прямой l (плоскости P). Векторы, параллельные одной прямой, называются коллинеарными, а векторы, расположенные в одной плоскости или параллельные одной и той же плоскости, – компланарными. Нулевой вектор считается коллинеарным любому вектору, так как он не имеет определенного направления.
называется параллельным прямой l (плоскости P), если либо он нулевой, либо прямая, проходящая через точки A и B, параллельна прямой l (плоскости P). Векторы, параллельные одной прямой, называются коллинеарными, а векторы, расположенные в одной плоскости или параллельные одной и той же плоскости, – компланарными. Нулевой вектор считается коллинеарным любому вектору, так как он не имеет определенного направления.
Два вектора  и
и  называются равными, если они коллинеарны, одинаково направлены и равны по длине. Равенство векторов
называются равными, если они коллинеарны, одинаково направлены и равны по длине. Равенство векторов  и
и  записывают так:
записывают так:  =
=  .
.
Из определения равенства векторов следует, что при параллельном переносе вектора получается вектор, равный исходному. Поэтому начало вектора можно перемещать в любую точку пространства.
Линейные операции над векторами.
П.1 Умножение вектора на число.
Определение 5.3 Произведением вектора  на число
на число  называется вектор
называется вектор  , имеющий направление вектора
, имеющий направление вектора  , если
, если  , и противоположное направление, если
, и противоположное направление, если  . Длина этого вектора равна произведению длины вектора
. Длина этого вектора равна произведению длины вектора  на модуль числа
на модуль числа  .
.
Из определения следует, что вектор  коллинеарен вектору
коллинеарен вектору  . Результат умножения вектора
. Результат умножения вектора  на число
на число  записывается равенством
записывается равенством  .
.
Свойства произведения вектора на число:
1) для любых чисел  и
и  и любого вектора
и любого вектора  справедливо равенство
справедливо равенство  ;
;
2) если вектор  , то для любого коллинеарного ему вектора
, то для любого коллинеарного ему вектора  существует, и при этом только одно, число
существует, и при этом только одно, число  , удовлетворяющее равенству
, удовлетворяющее равенству  .
.




