Найти интегралы:
1) 
2) 
3) 
4) 
Сделаем замену переменной 
тогда 
5) 
Совершим замену переменной 
6) 
Применяя метод замены переменной
тогда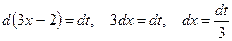 
7) 
Используя замену переменной 
тогда 
8) 
Произведем замену переменной 
тогда 
9) 
Сделаем замену переменной 
тогда
10) 
Произведем замену переменной 
тогда
11) 
Совершим замену переменной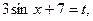 
тогда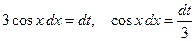 
12) 
Применяя метод замены переменной 
тогда 
13) 
Используя замену переменной тогда
14) 
Сделаем замену переменной 
тогда 
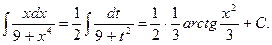
15) 
Произведем замену переменной 
тогда 
16) 
Совершим замену переменной 
тогда 
17) 
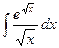
Применяя метод замены переменной 
тогда 
18) 
Используя замену переменной 
тогда 
19) 
Сделаем замену переменной тогда
20) 
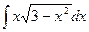
Произведем замену переменной 
тогда 
21) 
Применим формулу интегрирования по частям, полагая 
Тогда 
Положим 
и перейдем к непосредственному вычислению интеграла:
22) 
Выполним интегрирование по частям, полагая 
Тогда 
Вычислим исходный интеграл
23) 
Применим формулу интегрирования по частям, полагая 
Тогда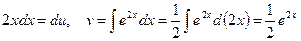 
.
Интеграл 
вычислим, применив еще раз формулу интегрирования по частям. Положим 
Тогда 
.
Исходный интеграл
24) 
Применим формулу понижения степени 
= 
25) 
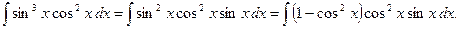
Сделаем замену переменной 
тогда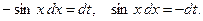 
26) 
Сделаем замену переменной 
, тогда 
27) 
Разложим подынтегральную функцию на простейшие дроби
Умножим обе части равенства на 
. Имеем 
Пусть 
, тогда 
. Пусть 
тогда 
.
Следовательно,
28) 
Разложим подынтегральную функцию на простейшие дроби:
Умножим обе части равенства на 
, получим 
.
Пусть 
, тогда 
.
Для нахождения 
и 
приравняем коэффициенты при степенях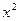 
и 
в обеих частях последнего равенства многочленов.
Получаем 
Исходный интеграл будет равен
+ 
Вычислить определенные интегралы.
29) 
30) 
31) 
Применим формулу интегрирования по частям, полагая 
.
Тогда 
.
32) 
Сделаем замену переменной 
то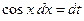 
.
33) Вычислить площадь фигуры, ограниченной линиями
Построим заданную фигуру (рис.1) и вычислим
.
34) Вычислить площадь фигуры, ограниченной графиками функций 
.
Построим графики заданных функций (рис.2)
Найдем точки пересечения графиков функций 
и 
: 
35) Вычислить объем тела, образованного вращением вокруг оси Oy фигуры, ограниченной графиками функций 
= 
36) Вычислить объем тела, образованного вращением вокруг оси Ox фигуры, ограниченной графиками функций 
Построим графики функций (рис.3)
, 
.
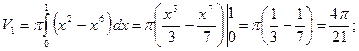
