Определение 3. Общим решением уравнения 
в некоторой области D плоскости 
называется функция 
, где C – произвольная постоянная, если выполняются следующие два условия:
1) для любого значения C функция является решением уравнения ;
2) для любой точки 
существует единственное значение постоянной 
такое, что справедливо равенство 
.
Если в общем решении зафиксирована константа C, то получившаяся функция называется частным решением. Задание начального условия позволяет определить значение постоянной C; она находится из равенства 
.
В некоторых случаях процесс решения приводит не к явному выражению для общего решения, а к соотношению вида 
, определяющему 
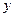как неявно заданную функцию от 
. Такое соотношение называется общим интегралом ДУ. Частное решение, представленное в неявном виде, называется частным интегралом.
3. Уравнения с разделяющимися переменными. Уравнением с разделяющимися переменными называется ДУ вида
(6)
или вида
. (7)
Уравнение (7) приводится к виду (6) умножением обеих его частей на 
. Уравнение (6) решается путем разделения переменных, для чего нужно поделить левую и правую часть (6) на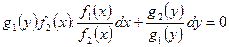 
. Интегрируя полученное ДУ, найдем общий интеграл уравнения (6). При разделении переменных предполагается, что 
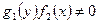. Если функции 
и 
имеют нули, то постоянные 
, где 
, могут являться решениями ДУ (6), что проверяется их подстановкой в (6). Эти дополнительные решения не всегда содержатся в общем интеграле уравнения (6).
4. Однородное уравнение. Функция 
называется однородной функцией n-го измерения, если при всех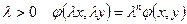 
. Однородным называется ДУ одного из двух видов: 1) 
, где 
однородные функции одного измерения; 2) 
, где 
однородная функция нулевого измерения. В частности, уравнение вида 
является однородным, так как 
однородная функция нулевого измерения: 
. Однородное ДУ интегрируется заменой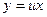 
, где 
новая неизвестная функция, отсюда 
. После подстановки этих выражений в ДУ получим уравнение с разделяющимися переменными относительно 
.
Рассмотрим уравнение вида
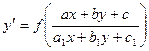. (8)
При
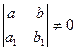
его можно свести к однородному с помощью замен 
. Постоянные 
и 
нужно выбрать так, чтобы уничтожить свободные члены в числителе и знаменателе дроби под знаком функции 
. В результате получим однородное уравнение 
. В случае
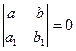
ДУ (8) приводится к уравнению с разделяющимися переменными подстановкой 
.
5. Уравнение Бернулли. Уравнением Бернулли называется ДУ вида
. (9)
Сделаем подстановку 
, здесь 
. Имеем 
; (9) запишется так: 
;
. (10)
Найдем какое-либо ненулевое решение вспомогательного ДУ 
(это уравнение с разделяющимися переменными, и оно имеет положительное частное решение 
). Подставив в (10) 
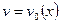, придем к уравнению с разделяющимися переменными 
или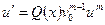 
. Если 
общее решение этого уравнения, то общее решение ДУ (9) найдем в виде 
.
6. Линейное ДУ первого порядка. Линейное ДУ первого порядка 
является частным случаем уравнения Бернулли (при m=0), поэтому для его интегрирования также можно применить подстановку .
7. Дифференциальное уравнение n-го порядка. Дифференциальным уравнением высшего (n-го) порядка называется уравнение вида
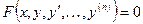(11)
(при условии, что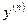 
присутствует в левой части (11)), 
. Решением ДУ (11) на интервале 
называется любая функция 
, определенная и раз дифференцируемая на , которая при подстановке в уравнение (11) обращает его в тождество на . Общее решение ДУ n-го порядка – это функция 
, которая при всех (допустимых) значениях 
является решением данного ДУ. При подстановке в общее решение вместо определенных числовых значений получаем частное решение ДУ. Начальные условия для ДУ n-го порядка имеют вид
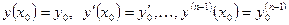, (12)
где 
заданные числа. Решить задачу Коши для ДУ высшего порядка – это значит найти его частное решение, удовлетворяющее заданным начальным условиям. Сформулируем теорему Коши для ДУ n-го порядка, разрешенного относительно n-ой производной
. (13)
Теорема Коши. Пусть функция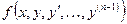 
определена, непрерывна и имеет непрерывные частные производные 
в открытой области D пространства 
. Тогда для любой точки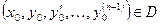 
существует решение 
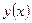задачи Коши (12), (13). Это решение единственно, т.е. если 
другое решение той же задачи Коши, то 
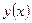для всех из пересечения интервалов, на которой определены и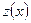 
.
Во многих случаях решение ДУ высшего порядка можно свести к решению ДУ более низкого порядка. Рассмотрим несколько типов ДУ, допускающих понижение порядка.
10. Уравнение вида 
. Интегрирование по обеих частей данного ДУ понижает его порядок на: 
. Применив этот прием раз, найдем выражение неизвестной функции 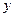через и произвольные постоянные , т.е. общее решение уравнения.
20. Уравнение вида 
(не содержащее явным образом функцию 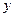и, возможно, несколько ее производных порядка ниже ). Подстановкой 
порядок ДУ понижается на 
единиц:
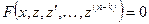. (14)
Пусть 
общее решение ДУ (14). Возвращаясь к функции 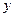, получаем уравнение типа 10 
, которое решается k-кратным интегрированием обеих частей.
30. Уравнение вида 
(не содержащее явно ). Подстановка 
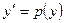понижает порядок уравнения на 1, поскольку при 
выражается через 
: 
и т.д.
Уравнение вида
(15)
называется линейным ДУ n-го порядка. Предполагается, что функции 
определены и непрерывны на некотором интервале . Если 
, уравнение (15) называется однородным, в противном случае – неоднородным.
Рассмотрим линейное однородное ДУ
, (16)
соответствующее неоднородному уравнению (15). Известно, что ДУ (16) всегда имеет n решений 
, образующих линейно независимую на систему функций. Такая система решений уравнения (16) называется фундаментальной. Это название объясняется тем фактом, что общее решение ДУ (16) имеет вид 
, где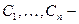 
произвольные постоянные. Общее решение линейного неоднородного уравнения (15) представляется формулой 
или 
, где 
какое-либо частное решение ДУ (15). Таким образом, для нахождения общего решения линейного неоднородного ДУ достаточно знать фундаментальную систему решений соответствующего ему однородного уравнения и одно (любое) частное решение 
неоднородного уравнения. Предположим, что фундаментальная система решений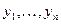 
ДУ уже известна. Универсальным способом нахождения является метод вариации произвольных постоянных, в котором частное решение (15) ищется в виде 
, где 
дифференцируемые функции аргумента 
. Производные этих функций находятся из системы линейных уравнений
которая имеет единственное решение. Зная 
, можно найти 
, а, значит, и 
.
Как видим, при решении линейного ДУ высшего порядка ключевую роль играет фундаментальная система решений соответствующего ему однородного ДУ. К сожалению, не существует общего метода построения фундаментальной системы ДУ (16). Такой метод можно указать в случае, когда в (16) функции 
постоянны, 
. Итак, рассмотрим линейное однородное ДУ с постоянными коэффициентами
, (17)
здесь 
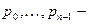постоянные числа. Все решения ДУ (17) определены на R. Характеристическим уравнением этого ДУ называется уравнение
. (18)
Как алгебраическое уравнение n-ой степени оно имеет n (вообще говоря, комплексных) корней. Пусть 
все корни уравнения (18), 
кратность корня 
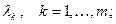тогда 
,
.
Каждому действительному корню 
поставим в соответствие 
функций 
, а каждой паре 
комплексно сопряженных корней (в этом случае 
) - 
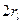функций 
(в частности, простому действительному корню соответствует одна функция 
, а простым комплексным корням 
две функции 
). Полученные таким образом n функций образуют фундаментальную систему решений ДУ (17). Если требуется решить линейное неоднородное ДУ с постоянными коэффициентами
, (19)
то его частное решение можно найти методом вариации произвольных постоянных, а в некоторых случаях – более простым методом неопределенных коэффициентов. Рассмотрим две ситуации, в которых применим последний метод.
1) Правая часть уравнения (19) имеет вид 
многочлен (здесь и далее индекс в обозначении многочлена указывает его степень). Тогда частное решение ДУ (19) следует искать в виде 
, где 
кратность корня 
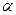характеристического уравнения (18), 
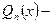многочлен с неопределенными (т.е. буквенными) коэффициентами.
2) Пусть в уравнении (19)
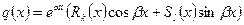, (20)
где 
многочлены. Обозначим через 
кратность корня 
уравнения (18), а через 
наибольшее из чисел 
. Тогда можно найти в виде 
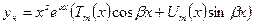, в котором 
многочлены с неопределенными коэффициентами.
Пояснения. 1. Если число 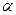в первой ситуации или во второй не является корнем уравнения (18), то множитель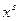 
в выражение не вводят (т.е. считают, что 
). 2. В виде (20) может отсутствовать 
(при 
) или 
(при 
). В первом случае полагают 
, во втором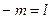 
. Подчеркнем, что в обоих случаях в выражение вводят и , и .
Пусть правая часть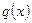 
уравнения (15) представляется в виде суммы нескольких функций: 
, и пусть 
частное решение ДУ
,
. Тогда сумма этих решений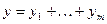 
является частным решением уравнения (15). Высказанное утверждение называется принципом суперпозиции решений и может быть использовано при решении линейных неоднородных ДУ.
ОБРАЗЦЫ РЕШЕНИЯ ПРИМЕРОВ
Дифференциальные уравнения 1-го порядка
