Метод эквивалентного генератора (МЭГ)

Метод контурных токов (МКТ)

Выбираем независимые контуры, т.е. ячейки, включающие в себя хотя бы одну ветвь, ранее не представленную в других контурах.

 

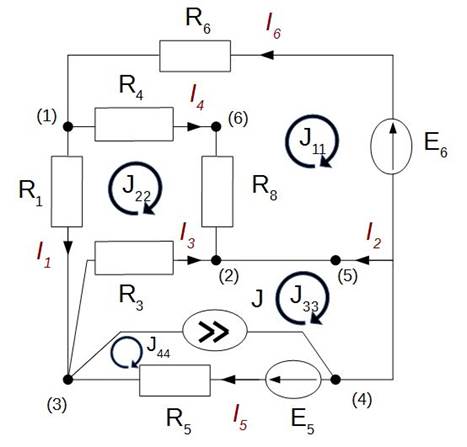
Число независимых контуров N определяется соотношением:

 

N = m-(n-1),

 

где m - число ветвей в схеме (их 8), n - число узлов в схеме (узлом считается соединение трёх и более ветвей, в нашем случае их 6).

 

На рисунке выше представлены произвольно выбранные независимые контуры и направления контурных токов в них. Ток J₄₄ протекает по ветви с источником тока,
и так как он единственный, то будет совпадать с заданным током источника.
Другими словами:

J₄₄ = J = 20 A

Следовательно, составлять уравнения по II-ому закону Кирхгофа имеет смысл лишь для трёх контуров. Для них данные уравнения примут вид:

J₁₁(R₄+R₆+R₈) - J₂₂(R₄+R₈) = -E₆

J₂₂(R₁+R₃+R₄+R₈) - J₁₁(R₄+R₈) - J₃₃R₃= 0

J₃₃(R₃+R₅) - J₂₂R₃= E₅ - JR₅

 

 

Рассчитаем систему уравнений методом Крамера и найдем контурные токи:

 

 

 

Теперь определим реальные токи в ветвях алгебраическим суммированием соответствующих контурных токов с учетом направления (контурные токи, совпадающие по направлению с направлением реального тока, учитываются
со знаком «+», встречные – со знаком «-»):

I₁=-J₂₂= 2.35 A I₄=J₂₂-J₁₁= 7.16 A

I₂=J₁₁-J₃₃= - 9.59 A I₅=J₃₃+J= 20.09 A

I₃=J₃₃-J₂₂= 2.43 A I₆=-J₁₁= 9.51 A

 

Проверка по первому закону Кирхгофа

I₁ = I₆ – I₄ = 9.51 – 7.16 = 2.35 А

I₂ = -I₃ – I₄ = -2.43 – 7.16 = -9.59 А

I₃ = I₁ + I₅ - J = 2.35 + 20.09 - 20 = 2.44 А

I₄ = I₆ – I₁ = 9.51 – 2.35 = 7.16 А

I₅ = -I₆ – I₂ + J = -9.51 + 9.59 + 20 = 20.08 А

I₆ = I₁ + I₄ = 2.35 + 7.16 = 9.51 А

Проверка по второму закону Кирхгофа

(1ый контур): -I₄(R₄+R₈) - I₆R₆ = -E₆ => -7.16*(21+9)-9.51*30 =-500

(2ой контур): I₄(R₄+R₈) - I₃R₃ - I₁R₁ = 0 => 7.16*(21+9)-2.43*40-2.35*50 = 0

(3ий контур): I₃R₃ + I₅R₅ = E₅ => 2.43*40+20.09*30 = 700

Все три выражения тождественны (с учётом небольшой погрешности вычислений), а значит токи найдены верно.

Составление баланса мощности

P_потр = I₁²R₁ + I₃²R₃ + I₄²(R₄+R₈) + I₅²R₅ + I₆²R₆

P_потр = 276.1 + 236.2 + 1537.97 + 12108.2 + 2713.2 = 16871 Вт

P_ген = E₅I₅ + E₆I₆ + J(I₅R₅-E₅)

P_ген = 14063 + 4755 – 1946 = 16872 Вт

P_потр = Р_ген

Баланс мощности составлен, с учётом погрешности мощность генерируемая равна мощности потребляемой.

Метод узловых потенциалов (МУП)

Количество уравнений для схемы в МУП равно n-1, где n - число неустранимых узлов (в нашем случае n =3).

Выбор узла, потенциал которого равен 0, обычно произволен. Однако, в нашем случае предлагается принять равным нулю потенциал 4-го узла.

Токи в ветвях с ненулевыми сопротивлениями определяются с помощью обобщенного закона Ома по найденным значениям потенциалов узлов цепи. Ток в ветви с сопротивлением, равным нулю, определяется из уравнения по I-му закону Кирхгофа, составленного для любого из узлов, к которым присоединена идеальная ветвь.

φ₂ = φ₄ = 0

φ₁(G₁+G₄₈+G₆)- φ₃(G₁)= E₆G₆

φ₃(G₁+G₃+G₅)- φ₁(G₁)= E₅G₅ - J

 

 

Теперь рассчитаем систему уравнений методом Крамераи найдем потенциалы:

 

 

 

т.е. φ₁ = 214.7 В
φ₃ = 97.4 В

 

Применяем обобщенный закон Ома и находим токи:

Для тока I₂ из уравнения по I-ому закону Кирхгофа для
второго узла:
- I₂ – I₄ – I₃ = 0
откуда I₂ = -I₄-I₃ = -7.159 - 2.435 = -9.59 А

 

 

 

 

Метод эквивалентного генератора (МЭГ)

По теореме об активном двухполюснике любая схема может быть представлена одной ветвью с ЭДС Е_экв и сопротивлением R_экв (параметрами эквивалентного генератора) относительно ветви с сопротивлением R и искомым током I. В результате, исходная схема преобразуется в одноконтурную, благодаря чему искомый ток определится

по формуле:

 

 

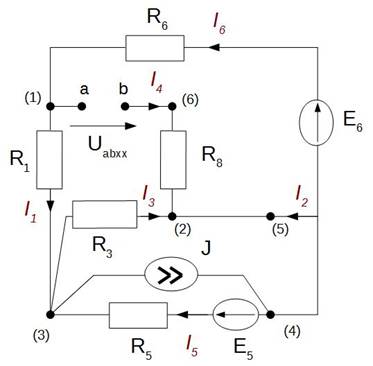1) Сначала определяем ЭДС эквивалентного генератора Е_экв. Для этого размыкается ветвь с искомым током. Любым удобным способом рассчитывается полученная схема и определяется напряжение холостого хода U_abxx в разрыве ветви с искомым током. Полученное напряжение и будеть определять величину и направление ЭДС эквивалентного генератора E_экв=U_abxx

 

 

В данной схеме удобнее искать U_abxx по методу двух узлов (частный случай метода узловых потенциалов). Для этого удаляем ветвь с разрывом, составляем уравнение напряжения на контуре по II-ому закону Кирхгофа через напряжение U_xx и ток I_6x и записываем уравнение напряжения U₃₄.

E_экв = U_хх
U_хх+I_6xR₆ = E₆
=> U_xx = E₆ – I_6xR₆

где I_6x = (-U₃₄ + E₆)/(R₁+R₆) = 4.54 А

U₃₄ = φ₃(G₁₆+G₃+G₅) — φ₄*0 = E₆G₁₆ + E₅G_{5 –} J

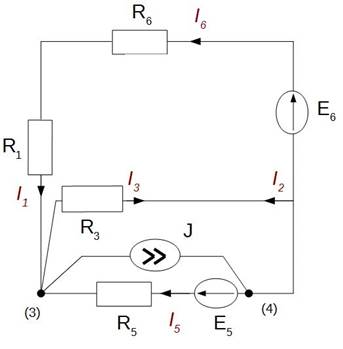возвращаясь к исходному,
Е_экв = U_xx = E₆ – I_6xR₆ = 363.3 В

 

 

2) Находим внутреннее сопротивление эквивалентного генератора R_экв.

Рассматриваемая схема преобразуется в пассивную, для чего все источники энергии удаляются из схемы, но сохраняются их внутренние сопротивления (на месте источника ЭДС остаются «провода», а на месте источников тока сохраняется «разрыв»). Рассчитывается входное сопротивление R_вх пассивной схемы относительно зажимов ветви с искомым током (без учета сопротивления этой ветви), определяющее сопротивление эквивалентного генератора (R_экв=R_вх=R_ab)_.

 

 

Зная E_экв и находим по описанной выше формуле:

= 7.16 А

Вывод: в результате выполнения расчетно-графического задания №1, мною были приобретены необходимые навыки анализа линейных электрических цепей постоянного тока, разработано умение применять различные методы для расчёта токов в электрических цепях (МКТ, МУП, МЭГ), а также умение проверять правильность расчетов при помощи законов Кирхгофа и составления баланса мощности.