Фермиондарға спиндері жартылай бүтін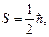 
, … барлық бөлшектер (электрондар, протондар, нейтрондар және т.б.) жатады. Бозондар – спиндері бүтін 
, 
, 
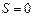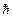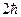, … бөлшектер (фотондар, фонондар, мөзондар және т.б.). Бұл жерде сыртқы магнит өрісі бағыты бойынша спиндерінің проекциялары көрсетілген. Себебі тәжірибе барысында тек қана проекцияларын ғана өлшейді, сондықтан көбінесе «спин» деп бұл шамалардың модулін емес, ал проекциясын айтады.
Фермиондар – Паули принципіне бағынатын өте айқын жекеше көрінетін бөлшектер. Бозондар керісінше, ұжымға бірігуге ұмтылады. Олар бір күйге шексіз орналаса алады, ол күйдегі бөлшектер көп болған сайын оған орналасуға тырысатын бөлшектер саны да соғұрлым көп болады. Ұжымның тұтастығына бөлшектер спецификасының қандай әсерлері бар? Бөлшектер спецификасы көріну үшін, оларды бір-бірімен кездесулері неғұрлым жиі болуы керек. «Кездесу» дегенді екі бөлшектің бір күйде немесе өте жақын күйлерде болуы деп түсіну керек.
бірдей бөлшектер 
күйде болсын дейік. Микробөлшектер өте сирек кездеседі, егер мына шарт орындалса
(3.5)
Бұл жағдайларда фермиондар мен бозондар спецификасын көрсетпейді, себебі әрбір бөлшек үшін көптеген еркін күйлер бар. Тұтас ұжым қасиеттері микробөлшектердің спецификасына байланысты болмайды. Мұндай ұжымдар азғындалмаған, ал (3.5) шарты азғындалмау шарты деп аталады.
Егер 
болса, онда күйді бірлеп немесе ұжымдап толтыру мүмкін болады. Бөлшектер спецификасы толық түрде көрінеді, егер тұтас ұжым қасиеттеріне жеткілікті түрде әсер ететін болсақ. Осындай ұжымдар азғындалған деп аталады.
Азғындалмаған ұжымдар қасиеттерін зерттейтін физикалық статистика классикалық статистика (Максвелл-Больцман статистикасы) деп аталады. Азғындалған ұжымдар қасиеттерін зерттейтін физикалық статистика кванттық статистика деп аталады. Фермиондардың квангтық статистикасы- Ферми-Дирак статистикасы, бозондардың статистикасы – Бозе-Эйнштейн статистикасы.
Бөлшектер санын азайтсақ немесе күй санын арттырсақ, онда азғындалған ұжым азғындалмаған ұжымға айналады. Бұл жағдайда бөлшектер спецификасына байланыссыз, ұжым Максвелл-Больцман статистикасына бағынады.
Таралу функциясы
Ұжым күйін сипаттау үшін оның термодинамикалық параметрлерін көрсету керек. Ұжымдағы бөлшектердің күйін білу үшін, олардың координаталары мен импульстерінің құраушыларын (немесе координаталар және импульстермен анықталатын бөлшектер энергияларын) көрсету қажет.
Осы екі түрлі шамалар арасындағы байланыс статистикалық таралу функциясы көмегімен іске асады, оны көбінесе энергия арқылы жазады:
(3.6)
Ол жүйедегі энергиялары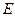 
ден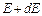 
-ге дейінгі бөлшектер санын көрсетеді, ал бөлшектердің күйі 
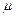және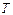 
параметрлерімен беріледі. Осындай функцияны толық статистикалық таралу функциясы деп атайды. Жазылуды жеңілдету үшін 
және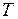 
белгіленулері индекс түрінде жазылады.
Толық таралу функциясын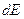 
интервалына сәйкес келетін күйлер саны 
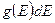-нің осы күйлердің бөлшектермен толтырылу ықтималдығы 
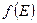көбейтіндісі ретінде де көрсетуге болады:
(3.7)
Көбінесе толық таралу функциясын 
деп те жазады, оны (3.7) теңдеуінің екі жағын да 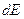-ге қысқарту арқылы алуға болады.
Физикада осы 
- таралу функциясы деп атайды. толтырылу ықтималдығы, сонымен қоса энергиясы 
-ге тең бір күйдегі бөлшектердің орташа санын да көрсетеді.
Мысалы. Жатақханадағы студенттердің толық таралу функциясын анықтау үшін этаждардағы бөлмелердің таралу функциясы 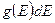-ны осы бөлмелердің толтырылу ықтималдылығы 
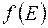-ге көбейтеміз.
