Учебная программа
«прикладная математика»
| № | Тема | Всего часов | Аудиторные | СР | Знания, умения | ||
| лек | лаб | ||||||
| ВТОРОЙ СЕМЕСТР | |||||||
| Введение 1. Латинский и греческий алфавиты 2. Координаты точки. Расстояния и углы, выраженные в координатах 3. | |||||||
Теория функций, графики, уравнения, неравенства
1. Функциональная зависимость. Способы задания функций.
2. Правая декартова система координат.
3. Линейная, квадратичная, показательная и логарифмическая функции, графики.
4. Линейные, квадратичные, показательные и логарифмические уравнения и неравенства, графические решения.
5. Функции второго порядка.
6. Дирак и его дельта функция.
7. Преобразования графиков функций: 
| |||||||
Тригонометрические функции.
1. Основные формулы.
2. Координатная плоскость, углы и их измерение, тригонометрические функции угла, радианная система измерения углов (дуг).
4. Основные теоремы тригонометрии: теорема синусов, теорема синусов, формулы приведения, тригонометрические функции двойного угла.
5. Прикладные аспекты основных теорем тригонометрии.
6. Тригонометрические функции числового аргумента:  ,  ,  ,  .
7. Графики тригонометрических функций.
8. Простейшие тригонометрические уравнения, общий случай тригонометрических уравнений, понятие арксинуса, арксинуса, арктангенса и арктангенса числа  для записи корней тригонометрических уравнений, тригонометрические уравнения, сводящиеся к простейшим.
| |||||||
| Уравнения движения точки. 1. Параметрическое задание функций. 2. Система параметрических уравнений, исключение параметра, приведение к каноническому виду. 3. Приложение тригонометрических функций (задачи на нахождение траектории движения точки при параметрическом задании движения). 4. Приложения тригонометрических функций к некоторым вопросам механики | |||||||
| Элементы векторной алгебры 1. Понятие вектора, свободный, скользящий и связанный. Примеры. 2. Простейшие операции над векторами. Геометрический способ сложения векторов. Примеры. 3. Координатный способ задания вектора, аналитические расчеты. 4. Радиус-вектор. Полярная система координат. Спираль Архимеда. | |||||||
Производная
1. Движение, путь, скорость
2. Производная. Простейшие примеры вычисления производных.
3. Табличное дифференцирование.
4. Уравнение касательной к кривой, заданной уравнением  в точке 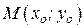 , нормаль.
5. Геометрическое значение производной. Построение графиков функций, используя производные.
6.Приближенное вычисление значений функции с помощью производной
| |||||||
| КОНТРОЛЬНАЯ РАБОТА | Зачет | ||||||
| ВСЕГО |
| ВТОРОЙ СЕМЕСТР | ||||||
| Техника интегрирования 1.Постановка задачи. Прямая и обратная задачи движения. 2. Простейшие интегралы. 3. Табличное интегрирование. 4. Определенные интегралы. Начальные условия. Интеграл и задача пути, пройденного точкой,элементарная работа, трение гибкого троса о шероховатую цилиндрическую поверхность, задача свободного падения тела без учета и с учетом сил в сопротивления среды. | ||||||
| Приложения высшей математики к некоторым вопросам физики и техники 1. Масса, центр тяжести плоских тел 2.Вычисление статических моментов, моментов инерции (нити, платины, диска) 3. Вычисление площадей плоских тел. Длина кривой, кривизна, вычисление длины кривой. | ||||||
| 9. | Дифференциальные уравнения 1. Геометрический смысл дифференциального уравнения первого порядка 2.Составление дифференциальных уравнений семейств кривых. Начальные условия задачи. 4. Линейные дифференциальные уравнения 1-ого порядка с разделяющими переменными. 3. Уравнение Бернулли | |||||
| 10. | Колебания 1. Движение под действием упругой силы, гармонические колебания, физический и математический маятник. | |||||
| 11. | Скалярное поле и градиент | |||||
| ВСЕГО | экзамен | |||||
| ИТОГО | Зачет/экзамен |
