Областное государственное бюджетное профессиональное образовательное
учреждение «Рязанский технологический колледж»
Экзаменационный
Материал
По математике.
Составители: Бутузова О.В., Башмакова И.Н., Калинина А.Б., Глебова О.В., Объедков Д.В
Структура экзаменационной работы.
1 часть – 1-7 задания – каждый по 1 баллу.
2часть – 8-17задания – каждый по 2 балла
18-21задания – каждый по 3 балла.
Критерии оценки:
0-9 баллов – «2»
10-20 баллов – «3»
21-30 баллов – «4»
31-39 баллов – «5»
Работа содержит 30 вариантов.
Вычислите.
1) 64 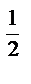 ·27
·27 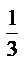 ; 7) 4
; 7) 4  :4
:4  ; 13) 3
; 13) 3  ·3
·3 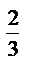 ; 19)
; 19) 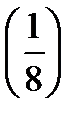 ·2
·2  ;
;
2)  :
:  8)
8) 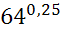 :
: 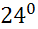 ; 14) 5
; 14) 5  ·25
·25  ; 20)
; 20)  ·
·  ;
;
3) 16  ·9
·9 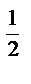 ; 9) 8
; 9) 8 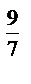 :2
:2 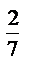 ; 15)
; 15) 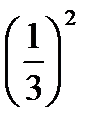 ·3
·3 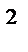 ; 21)
; 21) 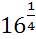 ∙
∙ 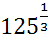
4) 2 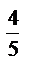 ·2
·2 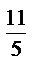 ; 10)3
; 10)3 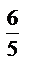 ·3
·3 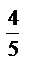 ; 16)
; 16) 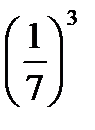 ·7
·7 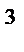 ; 22)
; 22) 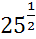 ∙
∙ 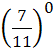
5) 5 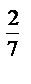 ·5
·5  ; 11)
; 11) 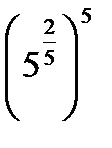 ; 17) 4
; 17) 4  ·4
·4 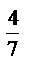 ; 23)
; 23) 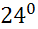 ∙
∙ 
6) 9 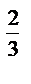 : 9
: 9 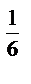 ; 12)
; 12) 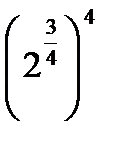 ; 18) 6
; 18) 6 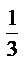 ·6
·6  ; 24)
; 24) 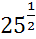 ∙
∙ 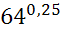
25. 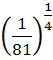 ∙
∙ 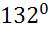 ;26)
;26) 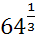 ∙
∙ 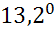 ; 27)
; 27) 
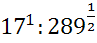 ;
;
28)  ∙
∙  ; 29)
; 29) 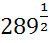 +
+ 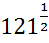 ; 30)
; 30)  ∙
∙  .
.
Решите уравнения.
1. 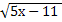 = 3; 2.
= 3; 2.  = 5; 3.
= 5; 3. 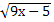 = 7; 4.
= 7; 4. 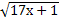 = 5;
= 5;
5. 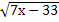 =4; 6.
=4; 6. 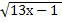 = 5; 7.
= 5; 7. 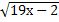 = 6; 8.
= 6; 8.  =
=  ; 9.
; 9. 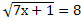 ; 10.
; 10. 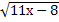 = 5; 11.
= 5; 11. 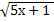 = 6; 12.
= 6; 12. 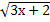 = 5;
= 5;
13. 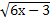 = 9; 14.
= 9; 14. 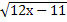 = 5; 15.
= 5; 15. 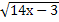 = 9; 16.
= 9; 16.  = 7;
= 7;
17. 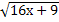 = 5; 18.
= 5; 18. 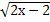 = 10; 19.
= 10; 19. 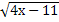 = 5; 20.
= 5; 20. 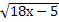 = 7;
= 7;
21.  = 3; 22.
= 3; 22. 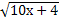 = 8; 23.
= 8; 23. 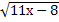 = 5; 24.
= 5; 24.  =7;
=7;
25. 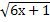 = 8; 26.
= 8; 26. 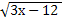 = 9; 27.
= 9; 27.  = 6; 28.
= 6; 28.  = 5;
= 5;
29. 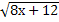 =10 30.
=10 30. 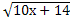 =4.
=4.
Решите показательное уравнения.
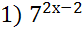 =
= 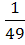 ; 2)
; 2) 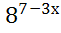 =
=  ; 3)
; 3) 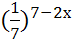 = 49; 4)
= 49; 4) 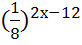 =64;
=64;
5) 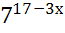 =
= 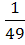 ; 6)
; 6)  = 81; 7)
= 81; 7)  =25; 8)
=25; 8)  =36;
=36;
9) 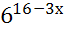 =
=  ; 10)
; 10) 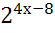 =
=  ; 11)
; 11) 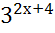 =
= 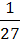 ; 12)
; 12)  =
=  ; 13)
; 13) 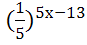 =25; 14)
=25; 14) 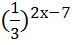 =81; 15)
=81; 15) 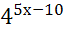 =1; 16)
=1; 16) 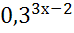 =1; 17)
=1; 17) 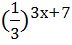 =(
=( ; 18)
; 18) 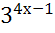 =
= 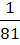 ; 19)
; 19) 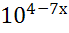 =
= 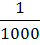 ; 20)
; 20)  =81; 21)
=81; 21) 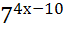 =
=  ; 22)
; 22)  =16; 23)
=16; 23)  =
=  ; 24)
; 24) 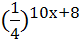 =16; 25)
=16; 25) 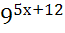 =
=  ;26)
;26) 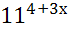 =
=  ; 27)
; 27)  =
= 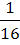 ;
;
28) 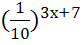 = 100; 29)
= 100; 29) 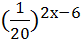 =400; 30)
=400; 30) 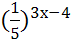 =(
=( .
.
Вычислите.
1. 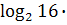
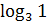 ; 2)
; 2) 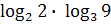 ; 3)
; 3) 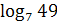 :
: 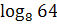 ; 4)
; 4) 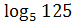 :
: 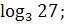
5) 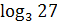 ∙
∙ 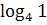 ; 5)
; 5)  ; 6)
; 6) 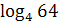 :
: 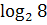 ;
;
7) 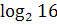 :
:  ; 8)
; 8) 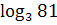 ∙
∙ 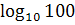 ; 9)
; 9) 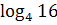 ∙
∙  ;
;
10) 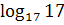 ∙
∙  ; 11)
; 11) 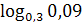 ∙
∙ 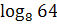 ; 12)
; 12) 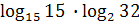 ;
;
13) 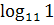 :
: 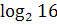 ; 14)
; 14) 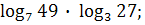 15)
15) 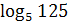 ∙
∙ 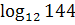 ;
;
16) 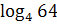 +
+ 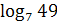 ; 17)
; 17) 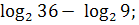 18)
18) 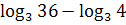 ;
;
19) 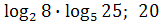 )
) 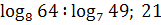 )
) 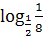 :
: 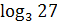 ;
;
22) 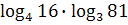 ; 23)
; 23) 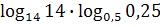 ; 24)
; 24) 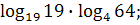
25)  ; 26)
; 26)  ; 27)
; 27) 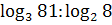 ;
;
28)  ; 29)
; 29) 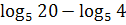 ; 30)
; 30) 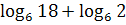 .
.
Решите тригонометрические уравнения.
1)  =
=  ; 2)
; 2) 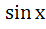 =
=  ; 3)
; 3)  =
=  ; 4)
; 4)  =
= 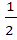 ; 5)
; 5)  =
=  ;
;
6)  =
= 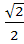 ; 7)
; 7) 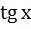 = 1; 8)
= 1; 8) 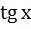 =>
=> 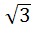 ; 9)
; 9)  =
= 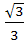 ; 10)
; 10) 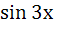 = 1;
= 1;
11) 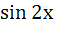 = -1; 12)
= -1; 12) 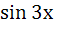 = 0; 13)
= 0; 13)  = 1; 14)
= 1; 14)  = -1;
= -1;
15)  = 0; 16)
= 0; 16)  = -
= -  ; 17)
; 17)  = -
= -  ; 18)
; 18) 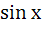 = -
= - 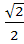 ; 19)
; 19) 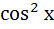 = 1;
= 1;
20) 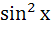 = 1; 21) 2
= 1; 21) 2  =
= 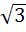 ; 22)
; 22) 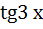 =
=  ; 23) 2
; 23) 2  =1;
=1;
24)) 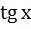 =
=  25)
25)  = - 1; 26)
= - 1; 26)  =1; 27)
=1; 27)  =0;
=0;
28)  = - 1; 29)
= - 1; 29) 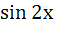 = 0; 30)
= 0; 30) 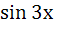 = 0;
= 0;
6. Найдите значение производной функции.
1.f(x)=4 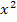 +3x-1 в точке x=3; 2. f(x)=4
+3x-1 в точке x=3; 2. f(x)=4 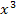 +3x-1 в точке x=2; 3. f(x)=
+3x-1 в точке x=2; 3. f(x)= 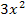 +4x-1 в точке x=3; 4. f(x)=
+4x-1 в точке x=3; 4. f(x)= 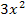 - 5x+5 в точке x=-3; 5. f(x)=
- 5x+5 в точке x=-3; 5. f(x)= 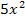 +6x-7 в точке x=-3; 6. f(x)=
+6x-7 в точке x=-3; 6. f(x)= 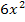 - 4x+5 в точке x=-3; 7. f(x)=t wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/></w:rPr><m:t>x</m:t></m:r></m:e><m:sup><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/></w:rPr><m:t>2</m:t></m:r></m:sup></m:sSup></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
- 4x+5 в точке x=-3; 7. f(x)=t wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/></w:rPr><m:t>x</m:t></m:r></m:e><m:sup><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/></w:rPr><m:t>2</m:t></m:r></m:sup></m:sSup></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 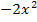 - 5x+5 в точке x=-3; 8. f(x)=
- 5x+5 в точке x=-3; 8. f(x)= 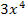 - 5x+5 в точке x=-1; 9. f(x)=
- 5x+5 в точке x=-1; 9. f(x)= 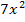 - 5x+5 в точке x=-2; 10.f(x)=
- 5x+5 в точке x=-2; 10.f(x)= 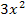 + 5x-12 в точке x=3; 11. f(x)=t wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/></w:rPr><m:t>x</m:t></m:r></m:e><m:sup><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/></w:rPr><m:t>4</m:t></m:r></m:sup></m:sSup></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
+ 5x-12 в точке x=3; 11. f(x)=t wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/></w:rPr><m:t>x</m:t></m:r></m:e><m:sup><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/></w:rPr><m:t>4</m:t></m:r></m:sup></m:sSup></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 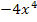 - 5
- 5 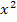 +5 в точке x=1; 12. f(x)=
+5 в точке x=1; 12. f(x)= 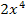 - 5x+5 в точке x=2; 13. f(x)=
- 5x+5 в точке x=2; 13. f(x)= 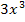 - 5
- 5 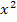 +5x в точке x=1; 14. f(x)=
+5x в точке x=1; 14. f(x)= 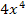 - 5
- 5 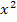 +5 в точке x=-1; 15. f(x)=t wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/></w:rPr><m:t>x</m:t></m:r></m:e><m:sup><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/></w:rPr><m:t>4</m:t></m:r></m:sup></m:sSup></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
+5 в точке x=-1; 15. f(x)=t wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/></w:rPr><m:t>x</m:t></m:r></m:e><m:sup><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/></w:rPr><m:t>4</m:t></m:r></m:sup></m:sSup></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 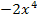 - 5x+5 в точке x= 2; 16. f(x)=t wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/></w:rPr><m:t>x</m:t></m:r></m:e><m:sup><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/></w:rPr><m:t>3</m:t></m:r></m:sup></m:sSup></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
- 5x+5 в точке x= 2; 16. f(x)=t wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/></w:rPr><m:t>x</m:t></m:r></m:e><m:sup><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/></w:rPr><m:t>3</m:t></m:r></m:sup></m:sSup></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">  - 5
- 5 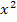 +5x в точке x=1; 17.f(x)=t wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/></w:rPr><m:t>x</m:t></m:r></m:e><m:sup><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/></w:rPr><m:t>2</m:t></m:r></m:sup></m:sSup></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
+5x в точке x=1; 17.f(x)=t wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/></w:rPr><m:t>x</m:t></m:r></m:e><m:sup><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/></w:rPr><m:t>2</m:t></m:r></m:sup></m:sSup></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 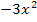 + 5x-12 в точке x=3; 18. f(x)=t wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/></w:rPr><m:t>x</m:t></m:r></m:e><m:sup><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/></w:rPr><m:t>4</m:t></m:r></m:sup></m:sSup></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
+ 5x-12 в точке x=3; 18. f(x)=t wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/></w:rPr><m:t>x</m:t></m:r></m:e><m:sup><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/></w:rPr><m:t>4</m:t></m:r></m:sup></m:sSup></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 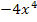 + 5
+ 5 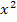 +5 в точке x=-1; 19. f(x)=
+5 в точке x=-1; 19. f(x)= 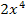 + 3x+5 в точке x=-2; 20. f(x)=
+ 3x+5 в точке x=-2; 20. f(x)= 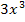 - 4
- 4 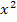 +5x в точке x= -1; 21. f(x) =t wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/></w:rPr><m:t>x</m:t></m:r></m:e><m:sup><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/></w:rPr><m:t>4</m:t></m:r></m:sup></m:sSup></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
+5x в точке x= -1; 21. f(x) =t wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/></w:rPr><m:t>x</m:t></m:r></m:e><m:sup><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/></w:rPr><m:t>4</m:t></m:r></m:sup></m:sSup></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">  - 5
- 5 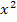 +6 в точке x= -1; 22. f(x)=
+6 в точке x= -1; 22. f(x)= 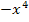 - 5x-6 в точке x=2; 23. f(x)=
- 5x-6 в точке x=2; 23. f(x)=  - 5
- 5 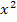 +5 в точке x=1; 24.f(x)=t wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/></w:rPr><m:t>x</m:t></m:r></m:e><m:sup><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/></w:rPr><m:t>2</m:t></m:r></m:sup></m:sSup></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
+5 в точке x=1; 24.f(x)=t wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/></w:rPr><m:t>x</m:t></m:r></m:e><m:sup><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/></w:rPr><m:t>2</m:t></m:r></m:sup></m:sSup></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 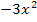 + 5x-10 в точке x=3; 25. f(x)=t wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/></w:rPr><m:t>x</m:t></m:r></m:e><m:sup><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/></w:rPr><m:t>4</m:t></m:r></m:sup></m:sSup></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
+ 5x-10 в точке x=3; 25. f(x)=t wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/></w:rPr><m:t>x</m:t></m:r></m:e><m:sup><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/></w:rPr><m:t>4</m:t></m:r></m:sup></m:sSup></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 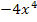 + 5
+ 5 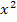 +5 в точке x=-1; 26. f(x)=
+5 в точке x=-1; 26. f(x)= 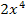 + 3x+5 в точке x=-2; 27. f(x)=
+ 3x+5 в точке x=-2; 27. f(x)= 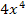 + 5
+ 5 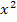 +6 в точке x=-1; 28. f(x)=
+6 в точке x=-1; 28. f(x)= 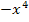 - 5
- 5 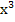 -6 в точке x=2; 29. f(x)=
-6 в точке x=2; 29. f(x)=  - 5
- 5 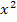 +5х в точке x=-1; 30. f(x)=t wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/></w:rPr><m:t>x</m:t></m:r></m:e><m:sup><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/></w:rPr><m:t>4</m:t></m:r></m:sup></m:sSup></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
+5х в точке x=-1; 30. f(x)=t wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/></w:rPr><m:t>x</m:t></m:r></m:e><m:sup><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/></w:rPr><m:t>4</m:t></m:r></m:sup></m:sSup></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 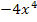 + 5
+ 5 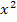 +5х в точке x=2;
+5х в точке x=2;
Решите задачу.
1.Измерения прямоугольного параллелепипеда 3;4;5.
Найдите объем этого параллелепипеда.
2. Измерения прямоугольного параллелепипеда 8;9;12.
Найдите объем этого параллелепипеда.
3. Измерения прямоугольного параллелепипеда 1;2;2.
Найдите объем этого параллелепипеда.
4. Измерения прямоугольного параллелепипеда 2;3;6.
Найдите объем этого параллелепипеда.
5. Измерения прямоугольного параллелепипеда 6;6;7.
Найдите объем этого параллелепипеда.
6. Измерения прямоугольного параллелепипеда 1;1;2.
Найдите объем этого параллелепипеда.
7. Измерения прямоугольного параллелепипеда 2;3;4.
Найдите объем этого параллелепипеда.
8. Измерения прямоугольного параллелепипеда 5;6;7.
Найдите объем этого параллелепипеда.
9. Измерения прямоугольного параллелепипеда 1;1;2.
Найдите площадь полной поверхности этого параллелепипеда.
10. Измерения прямоугольного параллелепипеда 6;6;7.
Найдите площадь полной поверхности этого параллелепипеда.
11. Измерения прямоугольного параллелепипеда 8;9;12.
Найдите площадь полной поверхности этого параллелепипеда.
12. Измерения прямоугольного параллелепипеда 3;4;5.
Найдите площадь полной поверхности этого параллелепипеда.
13. Измерения прямоугольного параллелепипеда 2;3;4.
Найдите площадь полной поверхности этого параллелепипеда.
14. Измерения прямоугольного параллелепипеда 5;6;7.
Найдите площадь полной поверхности этого параллелепипеда.
15. Измерения прямоугольного параллелепипеда 1;2;2.
Найдите площадь полной поверхности этого параллелепипеда.
16. Измерения прямоугольного параллелепипеда 2;3;6.
Найдите площадь полной поверхности этого параллелепипеда.
17. Измерения прямоугольного параллелепипеда 6;6;7.
Найдите длину диагонали этого параллелепипеда.
18. Измерения прямоугольного параллелепипеда 8;9;12.
Найдите длину диагонали этого параллелепипеда.
19. Измерения прямоугольного параллелепипеда 1;2;2.
Найдите длину диагонали этого параллелепипеда.
20. Измерения прямоугольного параллелепипеда 2;3;6.
Найдите длину диагонали этого параллелепипеда.
21. В правильной четырехугольной пирамиде сторона основания равна 3,
а высота 2. Найдите объем этой пирамиды.
22. В правильной четырехугольной пирамиде сторона основания равна 2,
а высота 3. Найдите объем этой пирамиды.
23. В правильной четырехугольной пирамиде сторона основания равна 1,
а высота 6. Найдите объем этой пирамиды.
24. В правильной четырехугольной пирамиде сторона основания равна 6,
а высота 1. Найдите объем этой пирамиды.
25. В правильной четырехугольной пирамиде сторона основания равна 6,
а высота 2. Найдите объем этой пирамиды.
26. В правильной четырехугольной пирамиде сторона основания равна 2,
а высота 6. Найдите объем этой пирамиды.
27. В правильной четырехугольной пирамиде сторона основания равна 3,
а высота 4. Найдите объем этой пирамиды.
28. В правильной четырехугольной пирамиде сторона основания равна 4,
а высота 3. Найдите объем этой пирамиды.
29. В правильной четырехугольной пирамиде сторона основания равна 3,
а высота 5. Найдите объем этой пирамиды.
30. В правильной четырехугольной пирамиде сторона основания равна 5,
а высота 3. Найдите объем этой пирамиды.
Определите.
1.Назовите вектор, начало и конец
которого являются вершинами
параллелепипеда ABCDA1B1C1D1,
равный сумме векторов AB и A1D1.
2. Назовите вектор, начало и конец
которого являются вершинами
параллелепипеда ABCDA1B1C1D1,
равный сумме векторов AB и AD1.
3.Назовите вектор, начало и конец
которого являются вершинами
параллелепипеда ABCDA1B1C1D1,
равный сумме векторов DA и B1B.
4.Назовите вектор, начало и конец
которого являются вершинами
параллелепипеда ABCDA1B1C1D1,
равный сумме векторов DB и DD1.
5.Назовите вектор, начало и конец
которого являются вершинами
параллелепипеда ABCDA1B1C1D1,
равный сумме векторов BC и DB1.
6.Назовите вектор, начало и конец
которого являются вершинами
параллелепипеда ABCDA1B1C1D1,
равный сумме векторов C1D1 и A1B.
7.Назовите вектор, начало и конец
которого являются вершинами
параллелепипеда ABCDA1B1C1D1,
равный сумме векторов C1D1 и DA.
8.Назовите вектор, начало и конец
которого являются вершинами
параллелепипеда ABCDA1B1C1D1,
равный сумме векторов BA1 и D1C1.
9.Назовите вектор, начало и конец
которого являются вершинами
параллелепипеда ABCDA1B1C1D1,
равный сумме векторов AD и A1B.
10.Назовите вектор, начало и конец
которого являются вершинами
параллелепипеда ABCDA1B1C1D1,
равный сумме векторов AD и D1C1.
11.Назовите вектор, начало и конец
которого являются вершинами
параллелепипеда ABCDA1B1C1D1,
равный сумме векторов AA1 и DC.
12.Назовите вектор, начало и конец
которого являются вершинами
параллелепипеда ABCDA1B1C1D1,
равный сумме векторов BA и D1C.
13.Назовите вектор, начало и конец
которого являются вершинами
параллелепипеда ABCDA1B1C1D1,
равный сумме векторов C1C и AB.
14.Назовите вектор, начало и конец
которого являются вершинами
параллелепипеда ABCDA1B1C1D1,
равный сумме векторов D1A1 и DC1.
15.Назовите вектор, начало и конец
которого являются вершинами
параллелепипеда ABCDA1B1C1D1,
равный сумме векторов AC и D1D.
16.Назовите вектор, начало и конец
которого являются вершинами
параллелепипеда ABCDA1B1C1D1,
равный сумме векторов AB и B1C.
17.Назовите вектор, начало и конец
которого являются вершинами
параллелепипеда ABCDA1B1C1D1,
равный сумме векторов DA и B1A1.
18.Назовите вектор, начало и конец
которого являются вершинами
параллелепипеда ABCDA1B1C1D1,
равный сумме векторов D1B и B1A1.
19.Назовите вектор, начало и конец которого являются вершинами параллелепипеда ABCDA1B1C1D1,
равный сумме векторов BB1 и A1D1.
20.Назовите вектор, начало и конец которого являются вершинами параллелепипеда ABCDA1B1C1D1,
равный сумме векторов DD1 и B1D1.
21.Назовите вектор, начало и конец которого являются вершинами параллелепипеда ABCDA1B1C1D1,
равный сумме векторов C1B1 и BD1.
22.Назовите вектор, начало и конец которого являются вершинами параллелепипеда ABCDA1B1C1D1,
равный сумме векторов B1A и DC.
23.Назовите вектор, начало и конец которого являются вершинами параллелепипеда ABCDA1B1C1D1,
равный сумме векторов A1D1 и DC.
24.Назовите вектор, начало и конец которого являются вершинами параллелепипеда ABCDA1B1C1D1,
равный сумме векторов CD и AB1.
25.Назовите вектор, начало и конец которого являются вершинами параллелепипеда ABCDA1B1C1D1,
равный сумме векторов B1A и D1A1.
26.Назовите вектор, начало и конец которого являются вершинами параллелепипеда ABCDA1B1C1D1,
равный сумме векторов C1D1 и A1A.
27.Назовите вектор, начало и конец которого являются вершинами параллелепипеда ABCDA1B1C1D1,
равный сумме векторов C1D и A1 B1.
28.Назовите вектор, начало и конец которого являются вершинами параллелепипеда ABCDA1B1C1D1,
равный сумме векторов AB и B1D.
29.Назовите вектор, начало и конец которого являются вершинами параллелепипеда ABCDA1B1C1D1,
равный сумме векторов B1A1 и CC1.
30.Назовите вектор, начало и конец которого являются вершинами параллелепипеда ABCDA1B1C1D1,
равный сумме векторов DD1 и C1A1.
№9 Вычислите.
1. 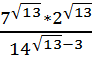
2. 
3. 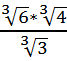
4. 
5. 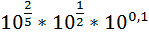
6. 
7. 
8. 
9. 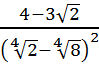
10. 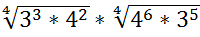
11. 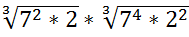
12. 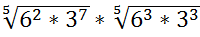
13. 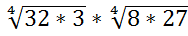
14. 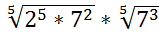
15. 
16. 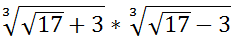
17. 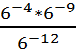
18. 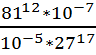
19. 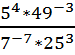
20. 
21. 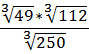
22. 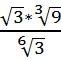
23. 
24. 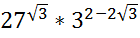
25. 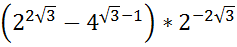
26. 
27. 
28. 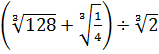
29. 
30.