Основные сведения о физических явлениях и процессах в полупроводниковых структурах

ФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ

Хабаровский институт инфокоммуникаций (филиал)

ГОУ ВПО «Сибирский государственный университет

телекоммуникаций и информатики»

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

К выполнению индивидуального задания

По курсу

«ФИЗИЧЕСКИЕ ОСНОВЫ ЭЛЕКТРОНИКИ»

Для студентов специальностей 210403.65, 210404.65, 210405.65, 210406.65

Хабаровск 2011 СОДЕРЖАНИЕ

 

1. Цель и задачи индивидуального задания 4

2. Основные сведения о физических явлениях и

процессах в полупроводниковых структурах 4

2.1. Вводные замечания 4

2.2. Основные понятия и уравнения твердотельной электроники 5

2.3. Электронно-дырочный переход 7

2.4. Структура металл-полупроводник 11

2.5. Структура металл-диэлектрик-полупроводник 14

3. Состав индивидуального задания 16

4. Указания по составлению пояснительной записки 17

4.1. Введение 17

4.2. Основная часть 17

4.3. Заключение 20

4.4. Библиографический список и требования к нему 21

Приложения 22

I. Варианты индивидуальных заданий 22

II. Темы рефератов 31

III. Пример оформления титульного листа 32

IV. Свойства кремния, германия и двуокиси кремния 33

ЦЕЛЬ И ЗАДАЧИ ИНДИВИДУАЛЬНОГО ЗАДАНИЯ

Индивидуальное задание (ИЗ) является промежуточным этапом в изучении курса «Физические основы микроэлектроники».

Целью выполнения ИЗ являются:

– выяснение физической сущности явлений и процессов, лежащих в основе работы различных полупроводниковых структур и дискретных полупроводниковых приборов, а также элементов интегральных микросхем (ИМС);

– приобретение практических навыков расчета электрофизических характеристик полупроводниковых структур;

– ознакомление со значениями параметров полупроводниковых материалов и их размерностями;

– развитие навыков самостоятельной работы с научно-технической литературой.

 

ОСНОВНЫЕ СВЕДЕНИЯ О ФИЗИЧЕСКИХ ЯВЛЕНИЯХ И ПРОЦЕССАХ В ПОЛУПРОВОДНИКОВЫХ СТРУКТУРАХ

2.1. Вводные замечания

В решении важнейших задач дальнейшего развития различных отраслей науки и техники исключительно большая роль отводится микроэлектронике, которая считается катализатором технического прогресса. Микроэлектроника родилась на стыке многих фундаментальных и прикладных наук, прежде всего физики, химии, математики, материаловедения и др.

Специалист, работающий в области микроэлектроники, должен иметь знания о ее физических, технологических и схемотехнических основах.

Микроэлектроника – это раздел электроники, охватывающий исследования и разработку качественно нового типа электронных приборов – интегральных микросхем и принципов их применения.

Основной задачей микроэлектроники является комплексная миниатюризация электронной аппаратуры – вычислительной техники, аппаратуры связи, устройств автоматики. Микроэлектронная технология позволяет резко расширить масштабы производства микроэлектронной аппаратуры, создать мощную индустрию информатики, удовлетворить потребности общества в информационном обеспечении.

Интегральные микросхемы, являющиеся элементной базой микроэлектроники, предназначены для реализации подавляющего большинства аппаратурных функций. Их элементы, аналогичные обычным радиодеталям и приборам, выполнены и объединены внутри или на поверхности общей подложки, электрически соединены между собой и заключены в единый корпус. Все или часть элементов создаются в едином технологическом процессе с использованием групповых методов изготовления.

Элементы полупроводниковой интегральной микросхемы – диоды, транзисторы, резисторы, конденсаторы – представляют собой совокупность различных полупроводниковых структур.

К таким полупроводниковым структурам относятся: контакты металл-полупроводник, электронно-дырочные переходы, структуры металл-диэлектрик-полупроводник (МДП). Физические явления и процессы в таких полупроводниковых структурах хорошо изучены и детально рассмотрены в научной и технической литературе.

 

2.2. Основные понятия и уравнения твердотельной электроники

Температурный потенциал:

,

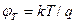где k – постоянная Больцмана (k =1,38⋅10-23Дж/К); T – абсолютная температура (при температуре T=300К температурный потенциал имеет значение 0,026В, или 26мВ), q – заряд электрона (q=1,6⋅10-19Кл).

Закон действующих масс:

,

где n – концентрация электронов; p – концентрация дырок; n_i – концентрация носителей заряда в собственном полупроводнике. Закон справедлив в случае термодинамического равновесия как для собственных, так и для примесных полупроводников.

Потенциал, характеризующий уровень Ферми в полупроводнике, равен:

или ,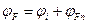

где – потенциал, соответствующий середине запрещенной зоны полупроводника; , – объемные потенциалы. Таким образом, согласно данным выражениям, в собственных полупроводниках (n = p = n_i) уровень Ферми расположен в середине запрещенной зоны, в электронных полупроводниках (n > n_i) – в верхней половине, а в дырочных (р > n_i) – в нижней половине запрещенной зоны.

Уровень Ферми одинаков во всех частях равновесной системы, какой бы разнородной она ни была, т. е. =const.

Закон полного тока в полупроводнике n-типа:

в полупроводнике р-типа:

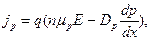
где и – градиент концентраций дырок и электронов; 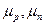подвижности дырок и электронов соответственно; 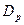и – коэффициенты диффузии дырок и электронов; – напряженность внешнего электрического поля.

Соотношение Эйнштейна, показывающее связь между коэффициентом диффузии и подвижностью носителей заряда,

,

в полупроводнике n- и p-типа соответственно.

Уравнение непрерывности для стационарных условий , выражающее закон сохранения частиц,

для полупроводников n- и p-типа, соответственно. Здесь и – избыточные (неравновесные) концентрации носителей заряда; g – скорость генерации носителей заряда под действием внешних факторов, например света; и – время жизни избыточных носителей заряда.

Время жизни неравновесных носителей заряда и равно промежутку времени, в течение которого их концентрация уменьшается в е раз.

Диффузионная длина носителей заряда соответствует расстоянию, которое они проходят за время жизни и равна:

и ,

где и 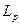– диффузионные длины электронов и дырок соответственно.

Уравнение Пуассона, позволяющее определить распределение потенциала в среде,

где - потенциал; – координата; – объемная плотность заряда; 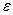– диэлектрическая проницаемость среды, для полупроводника 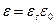, где – относительная диэлектрическая проницаемость полупроводника, – электрическая постоянная ( =8,85⋅10^-12Ф/м).

 

2.3. Электронно-дырочный переход

2.3.1. Электронно-дырочный переход (p-n-переход) – это контакт двух полупроводников с различным типом проводимости. Электропроводность полупроводников p-и n-типов определяется следующими выражениями:

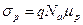, (1)

, (2)

где – электропроводность полупроводников p- и n-типов; – концентрация акцепторов и доноров соответственно.

Удельное сопротивление материала p-типа

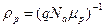
откуда

(3)

Аналогично концентрация доноров

(4)

При известных значениях и выражение для диффузионного потенциала (контактной разности потенциалов) может быть представлено в виде

. (5)

2.3.2. Вольтамперная характеристика (ВАХ) идеального p-n-перехода может быть описана следующим выражением:

(6)

где – ток насыщения; – приложенное напряжение. Ток насыщения определяется следующим выражением:

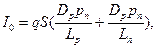(7)

где S – площадь p-n-перехода.

Когда , обратный ток насыщения определяется соотношением

, (8)

где W – ширина p-n-перехода.

Аналогичное выражение можно получить и для случая, когда .

Зависимость тока насыщения от температуры определяется выражением

(9)

где ; – ширина запрещенной зоны полупроводника; и – постоянные, определяемые свойствами полупроводника. Для p-n-перехода, сформированного на германии, . Для p-n-перехода, сформированного на кремнии, .

2.3.3. Определение дифференциального сопротивления p-n-перехода. Дифференцируя выражение (6) по напряжению и учитывая, что оно может быть представлено в виде

, (10)

можно получить

.

Если , то

.

Следовательно, дифференциальное сопротивление

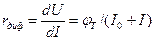(11)

или

(12)

При известном значении тока насыщения I ₀ расчет величины тока удобно производить с помощью выражения (11).

2.3.4. Определение барьерной емкости p-n-перехода. Величина удельной емкости резкого p-n-перехода в общем случае рассчитывается по формуле

. (13)

При этом толщина обедненного слоя (ширина p-n-перехода) определяется выражением

, (14)

где .

Для линейно-плавных переходов

(15)

где – градиент концентрации примесей.

Толщина обедненного слоя в этом случае находится по формуле

(16)

2.3.5. Определение напряжения пробоя 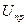для несимметричного резкого p-n-перехода. Величина максимального значения напряженности электрического поля в p-n-переходе определяется по формуле

(17)

При заданном значении толщина обедненного слоя p-n-перехода может быть найдена как 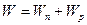, где

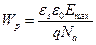
Напряжение пробоя для резкого несимметричного перехода

(18)

где – концентрация примеси в высокоомной области p-n-перехода.

Напряжение пробоя для линейно-плавных переходов

(19)

Оценка величины напряжения пробоя резкого p-n-перехода может быть сделана на основании приближенного выражения, справедливого для различных полупроводников:

В. (20)

Для линейно-плавных переходов величину напряжения пробоя можно оценить, используя соотношение

В. (21)

В выражениях (20), (21) размерность величин и а соответственно в см^-3 и см^-4, а ширины запрещенной зоны полупроводника в эВ.

 

2.4. Структура металл-полупроводник

4.1. Контакты на основе структуры металл-полупроводник обладают выпрямляющими свойствами в том случае, когда величина, равная разности работ выхода электронов из металла и полупроводника для полупроводника n-типа проводимости и для полупроводника p-типа проводимости. В этом случае обозначают и называют диффузионным потенциалом или контактной разностью потенциалов.

Согласно общей теории переноса носителей заряда в структурах металл-полупроводник (теории термоэлектронной эмиссии – диффузии) выражение для плотности тока имеет вид

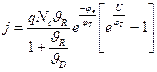. (22)

Здесь – скорость термоэлектронной рекомбинации носителей заряда на границе раздела структуры металл-полупроводник ( – эффективная постоянная Ричардсона, 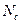– плотность электронных состояний в зоне проводимости полупроводника); – скорость дрейфа носителей заряда в обедненной области полупроводника ( – максимальное значение напряженности электрического поля в полупроводнике в области барьера Шоттки); – высота барьера Шоттки, равная для структуры металл-кремний n-типа проводимости, и для структуры металл- кремний p-типа проводимости.

Максимальное значение напряженности электрического поля в полупроводнике рассчитывается по формуле

(23)

при условии 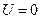, где W – толщина обедненного слоя полупроводника, U – напряжение смещения, т.е. .

В условиях равновесия W определяется выражением

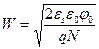, (24)

где N – концентрация основных носителей заряда в полупроводнике.

Если , то справедлива теория термоэлектронной эмиссии (теория Бете), и выражение для плотности тока (22) преобразуется к виду

. (25)

В том случае, когда 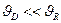, определяющим является процесс диффузии (теория Шоттки), и плотность тока с достаточной точностью вычисляется по формуле

. (26)

2.4.2. Для структуры металл-полупроводник распределение потенциала в области барьера Шоттки можно считать треугольным и аппроксимировать функцией

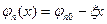, (27)

а распределение потенциальной энергии электрона

, (28)

где и – высота потенциального барьера в В и эВ, соответственно, т.е. высота барьера Шоттки. Тогда подстановка (28) в выражение для расчета вероятности квантовомеханического туннельного перехода электрона с энергией Е сквозь потенциальный барьер произвольной формы

(29)

позволяет получить выражение для расчета вероятности туннелирования электрона сквозь барьер Шоттки в виде

. (30)

В выражениях (29) и (30) – эффективная масса электронов в полупроводнике, кг; (Е – энергия электрона, туннелирующего из полупроводника в металл, эВ); h – постоянная Планка ( Дж⋅с); – напряженность электрического поля в полупроводнике, В/м, рассчитывается по формуле (23).

2.4.3. Барьерная емкость контакта металл-полупроводник определяется по формуле

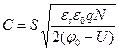, (31)

где S – площадь контакта металл-полупроводник.

 

2.5. Структура металл-диэлектрик-полупроводник

2.5.1. Структуру металл-диэлектрик-полупроводник можно рассматривать как конденсатор. Общую дифференциальную емкость МДП-структуры можно представить как последовательное соединение емкости диэлектрика C_d и переменной емкости C_n пространственного заряда у поверхности полупроводника

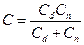(32)

Емкость пространственного заряда C_n зависит от величины поверхностного потенциала и плотности заряда в приповерхностной области полупроводника . Для идеальной МДП-структуры, не учитывающей наличие поверхностных состояний и предполагающей, что сопротивление диэлектрика является бесконечным, заряд Q_s можно выразить формулой

(33)

где – дебаевская длина, N – концентрация основных носителей заряда в полупроводнике.

Условие () перед этим выражением означает, что при следует воспользоваться знаком (+), а при – знаком (–).

Таким образом, емкость пространственного заряда

(34)

где

.

2.5.2. Для получения зависимости между приложенным к МДП-структуре напряжением U и общей емкостью C необходимо также знать зависимость между и U:

(35)

В (31) приняты следующие обозначения: U_D – падение напряжения на диэлектрике; U_ПЗ – напряжение плоских зон.

Падение напряжения на диэлектрике определяется выражением

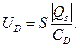(36)

С учетом разности работ выхода электрона из металла и полупроводника , а также при наличии поверхностных состояний Q_ss напряжение плоских зон определится как

(37)

2.5.3. Максимальная толщина обедненного слоя в приповерхностной области МДП-структуры в режиме сильной инверсии определяется

(38)

где или N_d в зависимости от типа проводимости полупроводника:

(39)

Для МДП-транзисторов с изолированным затвором важной величиной является напряжение включения или пороговое напряжение U_пор, при котором начинается сильная инверсия:

. (40)

В выражениях (39), (40) – объемный потенциал. Соответствующе U_пор значение дифференциальной емкости идеальной МДП-структуры равно

, (41)

где d – толщина диэлектрического слоя; – относительная диэлектрическая проницаемость диэлектрика.