Лабораторная работа №. Введение в табличный процессор Excel
Цель работы: Ознакомление с возможностями табличного процессора Excel. Ввод информации в рабочий лист и работа с ячейками. (4 часа.)
Табличный процессор Excel является одним из приложений группы Microsoft Office. Excel предоставляет пользователю широкие возможности по составлению и обработке финансовых и экономических моделей исостоит из типичных для среды Windows элементов, поддерживаемых ее стандартным графическим интерфейсом.
Функциональные возможности Excel настолько широки, что его, в отличие от обычных табличных редакторов, называют табличным процессором. Он поддерживает, в частности, следующие функции:
– обеспечивает создание, обработку и расчет разнообразных таблиц;
– позволяет осуществлять их редактирование, форматирование, использовать различные шрифты Windows;
– предоставляет средства для создания деловой графики (различные типы и форматы диаграмм с логарифмическим представлением данных, погрешностью и т.п.);
– обеспечивает совместимость со всеми программными продуктами семейства Microsoft Office;
– позволяет осуществлять сложные расчеты над числовыми рядами, матрицами, комплексными числами;
– предоставляет возможность работы с базами данных как непосредственно, так и с помощью специального языка запросов;
– облегчает "связывание" различных таблиц для сложных и объемных вычислений;
– обладает большим набором специальных функций для автоматизации обработки и расчетов (финансовые, информационные, логические, статистические, текстовые, математические и др.);
– позволяет использовать для создания деловой документации как стандартные шаблоны, так и шаблоны пользователя;
– обеспечивает обмен данными как внутри Excel, так и с другими приложениями Windows через: Буфер [Clipboard], протоколы Динамический Обмен Данными [ D ynamic D ata E xchange] (DDE), Связь и Внедрение Объектов [ O bject L ink E mbedded] (OLE) и преобразование форматов (программы фильтрации и конвертирования);
– позволяет автоматизировать наиболее употребляемые процессы за счет использования макрокоманд. Причем поддерживаются способы как автоматического создания команд, так и программирования с помощью специального встроенного языка Visual Basic;
– обладает большим количеством элементов управления (панелями, командами и командными кнопками, пиктограммами, флажками, переключателями и т.п.), которые облегчают работу пользователя;
– позволяет создавать демонстрационные Слайд-Шоу [Slides-Show] для презентаций, семинаров, конференций;
– облегчает возможность анализа данных с помощью Диспетчера Сценариев [Scenario Manager];
– предоставляет пользователю широкий набор Мастеров Подсказок [Master Wizard] и простой доступ к справочной информации через специальное меню Помощь [Help].
Общая схема работы в Excel совпадает со стандартными правилами работы с приложениями Windows.
Приведем принятые в Excel расширения файлов:
– XLS – файл рабочей книги (Sheet);
– XLC – файл деловой графики (Chart);
– XLW – файл рабочей книги в Excel 4.0 (WorkSheet);
– XLM – файл макротаблицы (Macro);
– XLT – файл шаблона (Template);
– XLA – файл дополнительных макрокоманд (Add-Ins);
– XLB – файл описания пиктографического меню (Tools Bar);
– XLL – файл библиотеки (Library).
Как запустить Excel. Для этого достаточно воспользоваться одним из способов запуска приложений из Windows, например, дважды щелкнув мышью по пиктограмме.
 |
На экране появится рабочее окно Excel 2007 со стандартными элементами интерфейса: полосами прокрутки, системным меню, полосой заголовка, строкой меню и лентой, соответствующей выбранному пункту меню (см. рис. 1.1.)
В отличие от других приложений, например Word, рабочая область, называемая в Excel Рабочий Лист [Worksheet], представляет собой таблицу, разделенную на строки и столбцы.
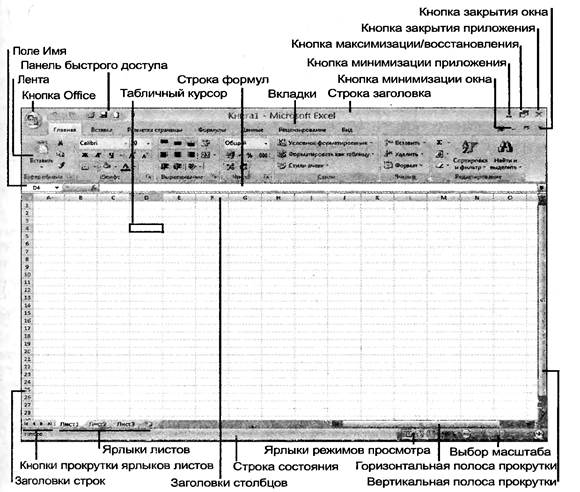
Рис. 1.1. Рабочий стол пакета Excel
Рассмотрим основные элементы рабочего листа:
– буквенная нумерация столбцов. Всего их в рабочем листе 16384: A, B, C,..., Z, AA,..., AZ, BA,..., BZ,..., XFD;
– цифровая нумерация строк. Всего в рабочем листе 1048576 строк;
– ячейка таблицы является минимальной единицей таблицы. Перемножив количество столбцов и строк получаем, что в рабочем листе 17 179 869 184 ячеек;
– строка заголовка документа. По умолчанию устанавливается заголовок Книга [Book] с указанием текущего номера открытого документа;
– строка формул. Это поле для представления текущей формулы;
– указатель ячейки по сути является более яркой рамкой, выделяющей текущую ячейку;
– поле адреса ячейки. Всегда содержит поле адреса текущей ячейки;
– ярлычок рабочего листа служит для листания рабочей книги, т.е., щелкнув мышью по видимому ярлычку листа ( стандартные имена Лист1, Лист2,...) (Sheet1, Sheet2, Sheet3,...) либо по стрелкам "Влево" или "Вправо" в горизонтальной строке, можно перейти к другому листу активной рабочей книги. Максимальное количество листов ограничивается пределом, связанным с объемом поддерживаемой памяти со стороны используемой версии Windows. Правый щелчок мышью по ярлычку рабочего листа инициирует открытие соответствующего меню с командами:
– Вставка [Insert]. Позволяет вставлять новый рабочий лист;
– Удалить [Delete]. Служит для удаления текущего листа;
– Переименовать [Rename]. Предназначается для переименования рабочего листа;
– Переместить/скопировать [Move or Copy]. Позволяет передвинуть или скопировать лист, например в другую рабочую книгу;
– Выбрать все листы [Select All Sheets]. Предназначается для выделения всех листов рабочей книги.
Двойной щелчок мышью по ярлычку рабочего листа инициирует появление диалогового окна для его переименования.
Как определить адрес ячейки. Вы можете определить адрес (т. е. указать место расположения) любой ячейки таблицы. Для этого необходимо указать номера столбца и строки, на пересечении которых расположена требуемая ячейка. Существует несколько способов определения адреса ячейки:
– Столбец-Строка. В этом случае первые символы определяют буквенный набор столбца (А, В,..., IV), остальные – числовой номер строки (1, 2,... ). Например, запись А1 определяет ссылку на ячейку, стоящую на пересечении столбца А и строки 1. Назовем этот способ адресации – относительная адресация;
– Перед обоими элементами адреса стоят символ доллара ($), $A$1, символ доллара ставится после выделения нужной ячейки путем нажатия на клавиатуре клавиши F4. Назовем этот способ адресации – относительная адресация. При копировании ячейки, содержащей формулу с абсолютной адресацией, вид формулы не меняется;
– Символ доллара стоит перед одним из элементов адреса ячейки $A1 (нажимаем два раза F4), или A$1 (нажимаем три раза F4). Назовем этот способ адресации – смешанной адресацией. При копировании ячейки, содержащей формулу, по какой-либо диагонали относительно этой ячейки, меняется тот элемент адреса, перед которым нет символа доллара;
– Строка-Столбец. Можно также пользоваться стилем ссылок, в котором нумеруются как строки, так и столбцы. Здесь ссылка на ячейку записывается следующим образом: символ R, за которым следует числовой номер строки, а затем символ С, за которым следует числовой номер столбца. В стиле ссылок R1C1 в Microsoft Excel положение ячейки обозначается буквой «R», за которой следует номер строки, и буквой «C», за которой следует номер столбца. Например, запись R1C1 означает ссылку на ячейку, стоящую на пересечении первой строки и первого столбца (эквивалент записи А1).
Стиль ссылок R1C1 удобен при вычислении положения столбцов и строк в макросах. Действие или набор действий, используемые для автоматизации выполнения задач. Макросы записываются на языке программирования Visual Basic для приложений (VBA).).
Чтобы включить или выключить стиль ссылок R1C1, нажмите кнопку Microsoft Office  , откройте диалоговое окно Параметры Excel, в категории Формулы в разделе Работа с формулами установите или снимите флажок Стиль ссылок R1C1.
, откройте диалоговое окно Параметры Excel, в категории Формулы в разделе Работа с формулами установите или снимите флажок Стиль ссылок R1C1.
Для перехода из одной ячейки в другую достаточно установить указатель мыши на требуемую позицию. Excel предоставляет также возможности для перемещения по рабочему листу с помощью клавиатуры (табл. 1.1.).
Таблица 1.1. Использование клавиатуры в Excel
| № п/п | Перемещение | Клавиши |
| Влево, вправо, вверх, вниз на одну ячейку | Влево, Вправо, Вверх, Вниз | |
| В самый левый (первый) столбец строки | Home | |
| В самый правый (последний) столбец строки | End | |
| На страницу вниз | PgDn | |
| На страницу вверх | PgUp | |
| В начало таблицы | Ctrl + Home | |
| В конец таблицы | Ctrl + End | |
| В верхнюю (первую) ячейку столбца | Ctrl + Вверх | |
| В нижнюю (последнюю) ячейку столбца | Сtrl + Вниз | |
| В левую (первую) ячейку строки | Ctrl + Влево | |
| В правую (последнюю) ячейку строки | Ctrl + Вправо | |
| Вниз по рабочему листу | Ctrl + PgDn | |
| Вверх по рабочему листу | Ctrl + PgUp |
Как выделить фрагмент в таблице. Выделение фрагмента осуществляется с помощью как мыши, так и клавиатуры (табл. 1.2.).
Для того чтобы выделить весь столбец или всю строку полностью нужно щелкнуть кнопкой мыши на заглавии столбца или строки.
Единичная ячейка, как и активная (текущая), выделяется на экране более яркой рамкой, фрагмент из двух и более ячеек – другим цветом. При этом активная ячейка в выделенном фрагменте обведена рамкой цвета выделения, но не закрашена.
Обратите внимание на то, что активной всегда считается одна ячейка! Снять выделение можно, щелкнув вторично мышью по выделенному фрагменту или нажав любую, не указанную в табл. 1.2., клавишу.
Таблица 1.2. Способы выделения фрагментов в Excel
| № п/п | Вид выделяемого фрагмента | Выделение фрагмента с помощью манипулятора "мышь" | Выделение фрагмента с помощью клавиатуры |
| Столбец | Установив курсор мыши на верхнюю ячейку столбца и перетянуть мышь по способу Drag&Drop в конец столбца | Установив курсор на верхнюю ячейку столбца нажать клавишу Shiftи установить курсор в конец выделяемого столбца | |
| Строка | Установив курсор мыши на левую ячейку строки и перетянуть мышь по способу Drag&Dropв конец строки | Установить курсор на левую ячейку строки нажать клавишу Shiftи установить курсор в конец выделяемой строки | |
| Несколько строк или столбцов, стоящих рядом | Установив курсор мыши на начальную ячейку выделяемого фрагмента и перетянуть его по способу Drag & Dropв конец фрагмента | Выделить столбец или строку, нажать клавишу F8 и, не отпуская ее, клавишами перемещения по тексту отметить требуемые позиции | |
| Единичная ячейка | Установив курсор мыши в требуемую ячейку и щелкнуть | Установить курсор в требуемую ячейку и нажать клавишу Enter | |
| Несколько фрагментов одновременно | 1. Выделить первый фрагмент. 2. Нажать клавишу Ctrl и не отпуская ее, выделить фрагмент до конца. 3. Отпустить клавишу Ctrl. Повторить шаги 2-3 столько раз, сколько необходимо | 1. Выделить первый фрагмент. 2. Нажать клавишу Ctrl и установить курсор в позицию следующего фрагмента. 3. Нажать клавишу Shift, а затем использовать клавиши перемещения по тексту для выделения фрагмента до конца. 4. Повторить шаги 2-4 столько раз, сколько необходимо | |
| Весь рабочий лист | 1. Установить курсор в самый верхний левый "пустой" прямоугольник и щелкнуть мышью | Нажать одновременно клавиши Ctrl+A |
Какие операции можно осуществлять над выделенными фрагментами. Выделенные фрагменты можно удалять ( клавиша Удалить [Del] ), копировать в Буфер команда Копировать [Copy] меню Правка [Edit] ), вырезать из рабочей книги и перемещать в Буфер ( команда Вырезать [Cut] меню Правка), восстанавливать из Буфера в рабочий лист ( команда Вставить [Paste] меню Правка), перемещать ( принцип Drag&Drop) и др.
Любая таблица состоит из заголовков (вертикальных и (или) горизонтальных) столбцов и (или) строк, и информации, хранящейся в ячейках на пересечении этих строк и столбцов. К дополнительным элементам таблиц можно отнести способы ее оформления (например, графы: утверждение, наименование, подпись и т. п.).
Как создать заголовок строки или столбца. Под созданием такого заголовка будем понимать ввод соответствующего текста в самую верхнюю ячейку столбца или самую левую ячейку строки. Для ввода текста в требуемую ячейку достаточно установить в нее указатель мыши (ячейка становится активной) и осуществить ввод необходимых символов с помощью клавиатуры.
Как изменить размеры ячейки. Если вас не удовлетворяет стандартный размер ячейки, вы можете изменить его по своему усмотрению одним из следующих способов:
– с помощью мыши. Установите указатель мыши на правый край начальной ячейки столбца (самой верхней) и, в соответствии с принципом Drag&Drop передвигая его по горизонтали, измените ширину столбца. Для изменения высоты строки достаточно выполнить аналогичные действия, установив указатель мыши на нижний край ячейки строки и передвигая ее по вертикали;
– с помощью команд меню Excel. Выделите в строке меню команду Формат [Format], пункт Столбец [Column], и зафиксируйте параметр Ширина [Width]. На экране откроется диалоговое окно Ширина столбца [Column Width]. В поле введите размеры столбца в символах. Для строки в команде Формат существует аналогичный пункт Строка [Row] с параметром Высота строки [Height].
Если необходимо установить стандартный размер ячеек для рабочей книги в меню Формат – Столбец инициируется параметр Стандарт [Standart] для ширины ячейки.
Для задания оптимальной ширины и высоты ячейки, при которой они будут определяться по длине и высоте введенного заголовка, можно воспользоваться параметром Автоподбор ширины и Автоподбор высоты [AutoFitSelection] в меню Формат – Столбец и Формат – Строка.
Если заголовок столбца или строки не помещается в установленный формат ячейки, то набранный вами текст заголовка, хотя и выйдет за пределы ячейки, но будет относится только к текущей ячейке. Активизировав стоящую рядом ячейку, вы автоматически делаете невидимой часть заголовка, превысившего размеры предыдущей ячейки. Текст в ячейке сохраняется.
Иногда заголовок столбца или строки удобнее записать в несколько строк. Для этого прежде всего следует увеличить размеры (по высоте и (или) ширине) ячейки, затем вызвать диалоговое окно Формат Ячейки [Format Cells] и, выделив в нем опцию Выравнивание [Alignment], щелкнуть мышью по кнопке выбора С заполнением [Fill].
Как заполнить ячейку таблицы. Прежде, чем заполнять ячейку, рекомендуем определить характер и параметры вводимой информации. Для этого лучше всего воспользоваться опциями команды Формат ячейки. Рассмотрим возможности, предоставляемые данной командой:
– Число [Numbering]. Служит для определения формата данных и состоит из следующих полей выбора:
– Категория [Category]. Указывает категорию – тип выбранного формата (пользовательский, бухгалтерский, научный, текстовый, дробный, процентный и т.п.);
– Код Формата [Format Codes]. Определяет код – возможную структуру информации согласно выбранному вами формату. Например, при выборе категории Число в поле выбора Код Формата появятся следующие коды числа:
# ##0
# ##0,00
P.;_# ##\_P_.
Выделив требуемую структуру, укажите необходимое представление информации в ячейке:
– Код [Code]. Служит для просмотра выбранного кода;
– Образец [Sample]. Предоставляет возможность предварительного просмотра выбранных формата и кода;
– Выравнивание [Alignment]. Указывает способ выравнивания информации в ячейке. Для этой цели предназначены следующие диалоговые области вывода:
– Горизонтальное [Horizontal]. Определяет вариант горизонтального выравнивания: Обычное [General], Слева [Left], Справа [Right], С заполнением [Fill], По обоим краям [Justify], Центрировать по выделению [Center across selection];
– Вертикальное [Vertical]. Указывает вариант вертикального выделения: По верхнему краю [Top], По центру [Center], По нижнему краю [Bottom], По обоим краям [Justify];
– Ориентация [Orientation]. Служит для определения ориентации информации в ячейке: по горизонтали слева направо; по вертикали сверху вниз; по вертикали слева направо, снизу вверх; по вертикали справа налево, сверху вниз;
– Переносить по словам [Wrap]. Определяет способ переноса текста внутри ячейки;
– Шрифт [Font]. Позволяет установить параметры шрифта вводимой информации;
– Рамка [Border]. Служит для выбора рамки таблицы и (или) ячейки;
– Вид [Pattern]. Предназначается для установки параметров изображения: закрашивание ячеек, цвет, узор, и т.п.;
– Защита [Protection]. Позволяет указать блокировку информации, которая будет хранится в ячейках. Для защиты можно выбрать пароль, без знания которого доступ к заблокированной информации невозможен.
После определения структуры вводимой информации можно осуществлять ее ввод в активную ячейку.
Заметим, что по умолчанию текстовая информация выравнивается по левому краю, а числовая – по правому.
Как сформировать название таблицы. Заголовок (название) таблицы обычно занимает одну или более строк и располагается в верхней части рабочего листа до заголовка столбцов и строк. Сформировать его можно с помощью следующих действий.
1. Установите указатель мыши в самую левую верхнюю ячейку таблицы.
2. Введите название таблицы, используя символ пробела для разделения строк.
3. Щелкните мышью по "галочке" в строке формул или просто нажмите клавишу Enter.
4. Если для названия таблицы требуется несколько строк, то необходимо повторить п. 1–3 для каждой новой строки.
Аналогичным образом можно ввести графы: утверждение, фирменная информация и т. п., в верхней части листа. Для изменения стиля оформления заголовка (шрифтов, размеров, расположения на бланке) можно выделить его одним из способов, предоставляемых Excel (см. табл. 1.2.) и отформатировать необходимым образом с помощью команд меню Формат.
Как сохранить документ на диске. Для этого достаточно воспользоваться стандартными командами Сохранить [Save] и Сохранить как [Save as] меню Файл [File].
Как прочитать ранее сохраненный документ с диска. Следует выполнить команду Открыть [Open] меню Файл.
Как снять сетку таблицы. Иногда удобнее работать с рабочим листом без координатной сетки. Для этого выбираем ленту Вид [View]. В диалоговой "выключите" кнопку выбора Сетка [Gridines] ("крестик" в этой прямоугольной кнопке пропадет). Выбрав кнопку OK, вы подтвердите свой выбор, после чего координатная сетка на рабочем листе исчезнет. Для ее восстановления достаточно снова "включить" данную кнопку выбора.
Как напечатать подготовленный документ. Для вывода на печать содержимого рабочего листа (книги) достаточно воспользоваться командой Печать [Print] меню Файл. Сначала с помощью команд этого же меню можно установить тип рабочего принтера (меню Выбор Принтера [Print Setup]), параметры страницы (меню Параметры страницы [Page Setup]). Для предварительного просмотра рабочего листа воспользуйтесь командой Предварительный просмотр [Print Preview]. При вызове ее на экране появится соответствующее диалоговое окно с опциями:
– Далее [Next] – служит для перехода к следующему фрагменту рабочего листа, если он не помещается в рабочем окне;
– Назад [Previous] – предназначается для вызова в рабочее окно предыдущего фрагмента листа;
– Масштаб [Zoom] – позволяет изменить размеры текущего изображения (увеличивать или уменьшать). Если щелкнуть мышью, то изображение увеличится ровно в два раза;
– Печать [Print] – посылает измененное изображение на печать;
– Страница [Setup] – вызывает диалоговое окно Параметры страницы;
– Поля [Margins] – определяет границы области печати, изменить которые можно, установив указатель мыши на рамку страницы и используя принцип Drag&Drop;
– Закрыть [Close] – закрывает данное диалоговое окно;
– Справка [Help] – позволяет просматривать справочную информацию.
Задание по лабораторной работе. Введите следующую таблицу:
| Амортизация по остаточной стоимости | |||
| Годы | Остаточная стоимость | Амортизация | Остаточная стоимость |
| (на начало периода) | 30% | (на конец периода) | |
Выполнение задания.
1. Переместите указатель мыши на ячейку C1 и щелкните левой кнопкой мыши. Наберите слова: Амортизация по остаточной стоимости
2. Нажмите клавишу Enter
3. В ячейку A3 введите слово: Годы
4. В ячейку B3 введите слова: Остаточная стоимость
5. В ячейку B4 введите слова: (на начало периода)
6. В ячейку E3 введите слова: Амортизация
7. В ячейку E4 введите слова: 30 %
8. В ячейку G3 введите слова: Остаточная стоимость
9. В ячейку G4 введите слова: (на конец периода)
10. Введите числа в ячейки:
в ячейку B6 – 600000; в ячейку E9 – 61740;
в ячейку B7 – 420000; в ячейку E10 – 43218;
в ячейку B8 – 294000; в ячейку G6 – 420000;
в ячейку B9 – 205800; в ячейку G7 – 294000;
в ячейку B10 – 144060; в ячейку G8 – 205800;
в ячейку E6 – 180000; в ячейку G9 – 144060;
в ячейку E7 – 126000; в ячейку G10 – 100842.
в ячейку E8 – 88200.
После ввода всей информации и данных получается таблица, приведенная на рис. 1.2.
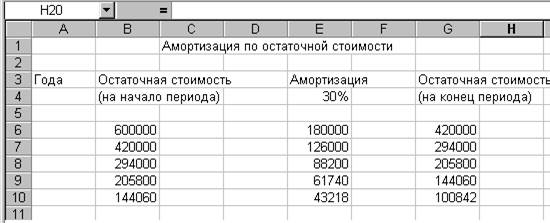
Рис. 1.2
Очевидно, что эта таблица представляет собой таблицу расчета остаточной стоимости оборудования при постоянном коэффициенте амортизации. На настоящий момент мы воспользовались пакетом Excel как обычной электронной пишущей машинкой. Получим эту таблицу, воспользовавшись возможностями Excel как табличного процессора.
Исходными данными для расчета амортизации являются остаточная стоимость в первый год (ячейка B6) и коэффициент амортизации (ячейка E4). Вся остальная таблица рассчитывается по очевидным формулам:
Величина амортизацииi = Остаточная стоимость (на начало периода)i *Коэффициент амортизации,
Остаточная стоимость (на конец периода) i = Остаточная стоимость (на начало периода) i – Величина амортизации i,
Остаточная стоимость (на начало периода) i+1 = Остаточная стоимость (на конец периода) i .
Поместим в ячейку B13 число 600000. В ячейку E13 введем формулу
=B13*E4.
В ячейке E13 появится число 180000. В ячейку G13 введем формулу
= B13-E13.
После этого в ячейке появится число420000. И, наконец, в ячейку B14 введем формулу
= G13.
В результате в этой ячейке получим число 420000.
Оставшуюся часть таблицы получим копированием содержимого ячеек. Так как процент амортизации у нас постоянный, то следует сделать так, чтобы адрес ячейки, содержащий значение процента амортизации, в процессе копирования не менялся. Для этого отредактируем формулу в ячейке E13. Сделаем адрес ячейки E4 абсолютным. Это осуществляется путем постановки перед номером столбца и строки символа доллара. Редактирование осуществляется в командной строке. Таким образом, команда примет следующий вид:
= B13*$E$4.
Затем пометим диапазон ячеек E13:G13. Для копирования поместим указатель мыши на квадратик заполнения в правом нижнем углу ячейки и, не отпуская нажатую левую кнопку мыши, протащим указатель мыши на четыре строчки вниз. Осталось только скопировать аналогичным образом формулу из ячейки B14. После копирования получим таблицу аналогичную ранее полученной.
Рассмотрим случай зависимости коэффициента амортизации от времени. Предположим, что коэффициент амортизации увеличивается с течением времени. Пусть этот коэффициент увеличивается каждый год на 10% (этот пример имеет только демонстрационный характер).
Поместим в ячейки A13:A14 цифры 1, 2. Это будут номера первого и второго годов. Дальнейшие номера введем в режиме автозаполнения. Для этого пометим ячейки A13:A14 и затем, поместив указатель мыши на квадратик копирования, протащим указатель на три ячейки вниз. В результате этих действий в ячейках A13:A17 получим номера годов, на которые рассчитывается амортизация.
Таким образом, режим автозаполнения это процесс ввода информации в интервал смежных ячеек по определенному алгоритму. В Excel, по умолчанию, реализован алгоритм арифметической прогрессии.
Можно заменить тип прогрессии. Для этого следует на вкладке Главная в группе Редактирование выберите команду Заполнить, а затем выберите в списке пункт Ряд.

В группе Тип выберите один из следующих вариантов.
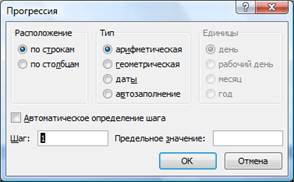
Линейная – для создания последовательности, в которой к каждому следующему значению прибавляется значение поля Шаг.
геометрическая – для создания последовательности, в которой каждое следующее значение умножается на значение поля Шаг.
Дата – для создания последовательности, в которой к каждой следующей дате прибавляется значение поля Шаг и которая зависит от единицы измерения, указанной в поле Единицы.
Автозаполнение – для создания такой же последовательности, как и с помощью маркера заполнения.
Для учета изменения коэффициента амортизации отредактируем формулу в ячейке E13 следующим образом
= B13*($E$4+(A13-1)*0,1).
После этого скопируем содержимое ячейки E13 в диапазон ячеек E14: E17. Таким образом, получаем таблицу учета амортизации с переменным коэффициентом амортизации.
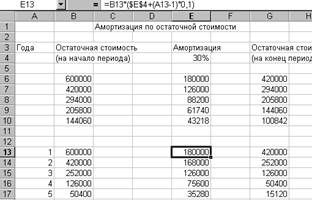
Рис.1.3
Уравнение регрессии
Решим задачу построения регрессионной модели. Рассмотрим функции рабочего листа, непосредственно вычисляющие различные характеристики линейного (разд. «Функции рабочего листа для уравнения линейной регрессии»), а затем и экспоненциального уравнения регрессии (разд. «Экспоненциальная модель»), которые позволяют значительно упростить процедуру регрессионного анализа для наиболее часто встречающихся на практике моделей.
Вы менеджер фирмы по продажам подержанных автомобилей и постоянно ведете учет проданных автомобилей. В вашем распоряжении имеются наблюдаемые величины: х – номер недели, у – число проданных за неделю автомобилей (табл. 7.1). Фирма совсем молодая, была создана шесть недель назад, и поэтому в вашем распоряжении имеется статистика только за этот весьма ограниченный промежуток времени.
Таблица 7.1. Значения наблюдаемых величин
| Наблюдаемые величины | Значения | |||||
| х | ||||||
| у |
Вы хотите сначала смоделировать ту динамику продаж, которая имеет место, а на основе построенной модели затем попытаться заглянуть в будущее, т.е. спрогнозировать ожидаемой объем продаж на ближайшие недели.
В качестве модели была принята простейшая, т.е. линейная. Таким образом, надо построить линейную модель  , наилучшим образом описывающую наблюдаемые значения. Обычно, т и b подбираются так, чтобы минимизировать сумму квадратов разностей теоретических и наблюдаемых значений зависимой переменной (у), т. е. минимизировать
, наилучшим образом описывающую наблюдаемые значения. Обычно, т и b подбираются так, чтобы минимизировать сумму квадратов разностей теоретических и наблюдаемых значений зависимой переменной (у), т. е. минимизировать
 ,
,
где n – число наблюдений (в данном случае n = 6).
Для решения этой задачи:
1. Заполните ячейки как показано на Рис. 7.8;
2. Отведите под переменные т и b ячейки D2 и Е2.
, 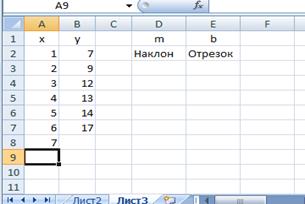
Рис. 7.8.
Функции рабочего листа для уравнения линейной регрессии
Параметры т и b линейной модели y = тх + b можно определить при помощи функций НАКЛОН (SLOPE) и ОТРЕЗОК (INTERCEPT).
Функция НАКЛОН (SLOPE) определяет коэффициент наклона линейного тренда, а функция ОТРЕЗОК (INTERCEPT) – точку пересечения линии линейного тренда с осью ординат.
Синтаксис:
НАКЛОН (изв_знач_у; изв_знач_х)
ОТРЕЗОК (изв_знач_у; изв_знач_х)
изв_знач_у – массив известных значений зависимой наблюдаемой величи ны;
изв_знач_х – массив известных значений независимой наблюдаемой величины.
Если изв_знач_х опущены, то предполагается, что это массив {1; 2; 3;...} такого же размера, как и изв_знач_у.
Функции НАКЛОН и ОТРЕЗОК вычисляют результат по следующим формулам:

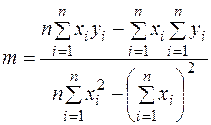 ,
,
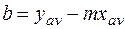 ,
,
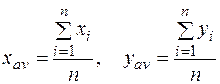 .
.
В ячейках D3 и Е3 (рис. 7.9) найдены значения т и b, соответственно, по формулам
=НАКЛОН (B2:B7;A2:A7)
=ОТРЕ3ОК(B2:B7;A2:A7)
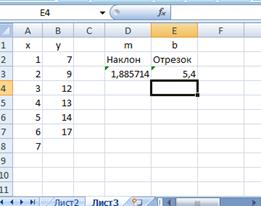
Рис. 7.9. Коэффициенты уравнения регрессии
Найдя коэффициенты уравнения регрессии, на их основе легко определить теоретические значения наблюдаемой величины, для этого:
1. Введите в ячейку С2 формулу
=$D$3*A2+$E$3
2. Выберите ячейку С2, расположите указатель мыши на маркере заполнения и протяните его на диапазон C3:C7 (рис. 7.10).
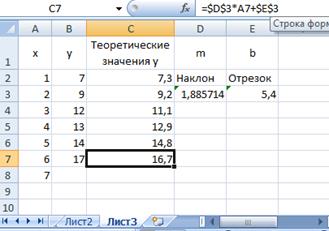
Рис. 7.10. Теоретические значения линейной регрессии,
вычисленные по функциям рабочего листа
Теоретическое значение можно вычислить с помощью функции ПРЕДСКАЗ (FORECAST), не определяя предварительно коэффициенты линейной модели, в фиксированной точке.
Синтаксис:
ПРЕДСКАЗ (х; изв_знач_у; изв_знач_х)
§ х точка данных, для которой предсказывается значение;
§ изв_знач_у – массив известных значений зависимой наблюдаемой величины;
§ изв_знач_х – массив известных значений независимой наблюдаемой величины. Если изв_знач_х опущены то предполагается, что это массив {1; 2; 3;...} такого же размера, как и изв зна ч_у.
Например теоретическое значение в ячейке С2 можно было бы также определить по формуле
=ПРЕДСКАЗ(А2;$B$2:$B$7;$A$2:$A$7).
Введем эту формулу в ячейку F2 и протянем ее на диапазон F3:F7 (рис. 7.11).
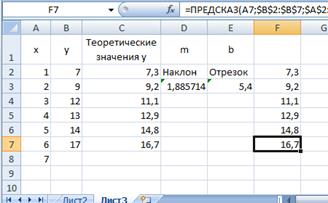
Рис. 7.11.
Функция ТЕНДЕНЦИЯ (TREND) вычисляет значения уравнения линейной регрессии для целого диапазона значений независимой переменной как для случая одномерного, так и многомерного уравнения регрессии. Многомерная линейная модель регрессии имеет вид:
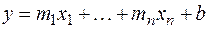 .
.
Синтаксис:
ТЕНДЕНЦИЯ (изв зна чу; иэв_зна ч_х; нов зна чх; константа)
§ изв_знач_у – массив известных значений зависимой наблюдаемой величины;
§ изв_знач_х – массив известных значений независимой наблюдаемой величины. Если изв_знач_х опущены, то предполагается, что это массив {1; 2; 3;...} такого же размера, как и изв_знач_у;
§ нов_знач_х – новые значения х, для которых ТЕНДЕНЦИЯ возвращает соот. ветствуюшие значения у;
§ константа – логическое значение, которое указывает, требуется ли, чтобы константа b была равна 0. Если константа имеет значение ИСТИНА или опущена, то b вычисляется обычным образом. Если константа имеет значение ЛОЖЬ, то b полагается равным 0.
Если строится многомерная линейная модель, то изв_знач_х и нов_знач_х должны содержать столбец (или строку) для каждой независимой переменной. Если нов_знач_х опущены, то предполагается, что они совпадают с изв_знач_х.
В ячейку С7 введем формулу массива
={ТЕНДЕНЦИЯ($B$2:$B$7;$A$2:$A$7;A10:A12)}
(не забудьте ее ввод завершить нажатием комбинации клавиш <Shift>+<Ctrl>+<Enter>) (рис. 7.12).
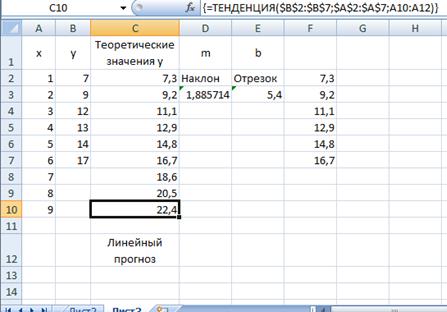
Рис. 7.12.
Функция ЛИНЕЙН(LINEST) возвращает массив { mn, …, m1, b }значений параметров уравнения многомерной линейной регрессии.
Синтаксис:
ЛИНЕЙН(изв_знач_у; изв_знач_х; константа; стат)
v изв_знач_у – массив известных значений зависимой наблюдаемой величины;
v изв_знач_х – массив известных значений независимой наблюдаемой величины. Если изв_знач_х опущены, то предполагается, что это массив {1; 2; 3;...} такого же размера, как и изв_знач_у;
v константа – логическое значение, которое указывает, требуется ли, чтобы константа b была равна 0. Если константа имеет значение ИСТИНА, или опущена, то b вычисляется обычным образом. Если константа имеет значение ЛОЖЬ, то b полагается равным 0;
v стат – логическое значение, которое указывает, требуется ли вернуть дополнительную статистику по регрессии, например коэффициент корреляции. Если стат имеет значение ИСТИНА, то функция ЛИНЕЙН возвращает дополнительную регрессионную статистику. Если стат имеет значение ЛОЖЬ или опущена, то функция ЛИНЕЙН возвращает только значения коэффициентов.
Теперь настало время построить его диаграмму. В MS Excel уравнения регрессии называется линией тренда, которая показывает тенденцию изменения данных и служит для составления прогнозов. Для создания линии тренда на основе диаграммы используется один из пяти типов аппроксимации или линейная фильтрация (табл. 7.2).
Таблица 7.2. Типы аппроксимаций
| Тип | Описание |
| Линейная | y = mx + b где т – тангенс угла наклона, b – точка пересечения с осью ординат |
| Логарифмическая | y= c ln x + b где c и b – константы |
| Полиномиальная | y = c6 x6 + … + c1 x + b где с6,..., с1 и b – константы |
| Степенная | y = c xb где с и b – константы |
| Экспоненциальная | у = c e bx где с и b – константы |
| Линейная фильтрация | Каждая точка данных на линии тренда строится на основе среднего указанного числа точек данных (периодов). Чем больше число периодов устанавливается, тем более гладкой, но менее точной, становится линия тренда |
На диаграмме можно выделить любой ряд данных и добавить к нему линию тренда. Когда линия тренда добавляется к ряду данных, она связывается с ним, и поэтому при изменении значений любых точек ряда данных линия тренда автоматически пересчитывается и обновляется на диаграмме.
Кроме того, имеется возможность выбирать точку, в которой линия тренда пересекает ось ординат, добавлять к диаграмме уравнение регрессии и величину достоверности аппроксимации.
Покажем на нашем примере по продажам автомобилей, как строится линия тренда. Для этого:
1. При помощи Мастера Диаграмм постройте по диапазону ячеек А2:В7 точечный график.
2. Выберите диаграмму или график, а затем команду Диаграмма → Добавить линию тренда. На экране отобразится диалоговое окно Линия тренда.
3. На вкладке Тип диалогового окна Линия тренда выберите тип линии тренда. В данном случае – Линейная (рис. 7.13).

Рис. 7.13. Вкладка Тип диалогового окна Линия тренда
4. На вкладке Параметры диалогового окна Линия тренда можно установить параметры линии тренда (рис. 7.14). В группе Прогноз можно указать число периодов, на которые линия тренда либо составляет прогноз, либо определяет историю процесса. Если вы отметите флажок показывать уравнение на диаграмме, то уравнение линии тренда отобразится на диаграмме. Если установите флажок поместить на диаграмму величину достоверности аппроксимации (R^2), то на диаграмме отобразится величина достоверности аппроксимации, т.е. квадрат коэффициента корреляции. По коэффициенту корреляции можно судить о правомерности использования линейного уравнения регрессии. Если он лежит в диапазоне от 0,9 до 1, то данную зависимость можно использовать для предсказания результата. Чем коэффициент корреляции ближе к единице, тем он более обосновано указывает на линейную зависимость между наблюдаемыми величинами. Если коэффициент корреляции лежит близко к –1, то это говорит об обратной зависимости между ними. Флажок пересечение кривой с осью Y в точке устанавливается только в том случае, когда эта точка известна. Например, если данный флажок включен и в соответствующее поле введено значение 0, то это означает, что ищется модель y = bx.
5. Нажмите на кнопку ОК.
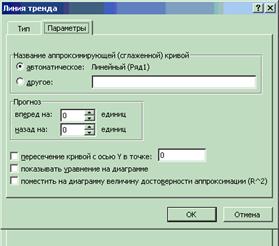
Рис. 7.14. Вкладка Параметры диалогового окна Линия тренда
Результат выполнения команды Добавить линию тренда приведен на рис. 7.15. Квадрат коэффициента корреляции равен 0.9723. Следовательно, линейная модель может быть использована для предсказания результатов.

Рис. 7.15. Линия тренда
Экспоненциальная модель
Другой часто встречающейся на практике регрессионной моделью является экспоненциальная, описываемая уравнением
у = c ebx.
Значения экспоненциального тренда можно предсказывать при помощи функции РОСТ(GROWTH).
Синтаксис:
РОСТ (изв_знач_у; изв_знач_х; нов_знач_х; константа)
изв_знач_у – массив известных значений зависимой наблюдаемой вели. чи ны;
изв_знач_х – массив известных значений независимой наблюдаемой величины. Если изв_знач_х опущены, то предполагается, что это массив {1; 2; 3;...} такого же размера, как и изв_знач_у;
нов_знач_х – новые значения х, для которых рост возвращает соответствующие значения у;
константа – логическое значение, которое указывает, требуется ли, чтобы константа b была равна 0. Если константа имеет значение ИСТИНА или опущена, то b вычисляется обычным образом. Если константа имеет значение ЛОЖЬ, то b полагается равным 0 (рис. 7.16).
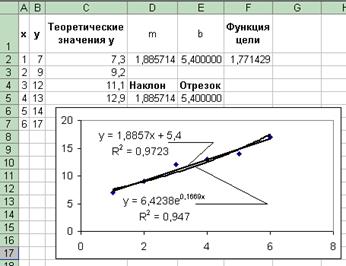
Рис. 7.16. Связь между линейной и экспоненциальной линиями тренда
Значения параметров экспоненциальной модели определяются при помощи, функции ЛГРФПРИБЛ (LOGEST).
Синтаксис:
ЛГРФПРИБЛ (изв_знач_у; изв_знач_х; константа; стат)
изв_знач_у – массив известных значений зависимой наблюдаемой вели. чи ны;
изв_знач_х – массив известных значений независимой наблюдаемой величины. Если изв_знач_х опущены, то предполагается, что это массив {1; 2; 3;...} такого же размера, как и изв_знач_у;
нов_знач_х – новые значения х, для которых рост возвращает соответствующие значения у;
константа – логическое значение, которое указывает, требуется ли, чтобы константа b была равна 0. Если константа имеет значение ИСТИНА или опущена, то b вычисляется обычным образом. Если константа имеет значение ЛОЖЬ, то b полагается равным 0;
стат – логическое значение, которое указывает, требуется ли, вернуть дополнительную статистику по регрессии, например коэффициент корреляции. Если стат имеет значение ИСТИНА, то функция ЛГРФПРИБЛ возвращает дополнительную регрессионную статистику. Если стат имеет значение ЛОЖЬ или опущена, то функция ЛГРФПРИБЛ возвращает только значения коэффициентов.
Одномерную экспоненциальную модель также можно построить графически, как это было описано в разд. “Построение уравнения регрессии” ранее в этом разделе.
Линейный и экспоненциальный тренды тесно связаны между собой. Покажем это на рассматриваемом в данном разделе примере с продажами автомобилей.
Квадрат коэффициента корреляции экспоненциальной модели равен 0.947 и меньше квадрата коэффициента корреляции линейной модели. Таким образом, в данном случае линейная модель более достоверно описывает зависимость между наблюдаемыми величинами.
В Excel 2007 после построения графика зависимости продаж от недели (рис. 7.17) построение линии тренда осуществляется следующим образом.

Рис. 7.17.
После щелчка правой кнопкой мыши по одному из маркеров данных выбираем из появившегося меню пункт Добавить линию тренда (рис. 7.18).
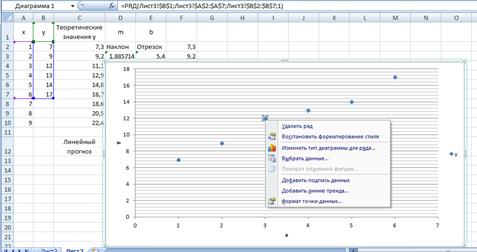
Рис. 7.18.
В появившемся окне выбираем тип линии тренда (Линейная), Показать уравнение на диаграмме и Поместить на диаграмму величину достоверности аппроксимации (рис. 7.19).
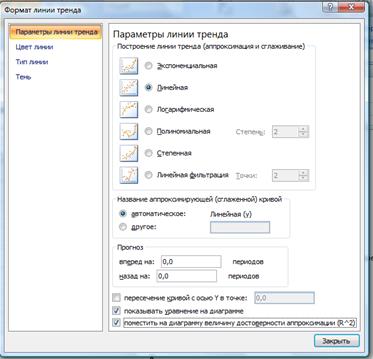
Рис. 7.19.
Результат показан на рис. 7.20.
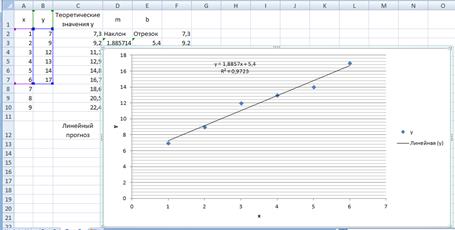
Рис. 7.20.
Аналогичным образом строим экспоненциальную модель (рис. 7.21).
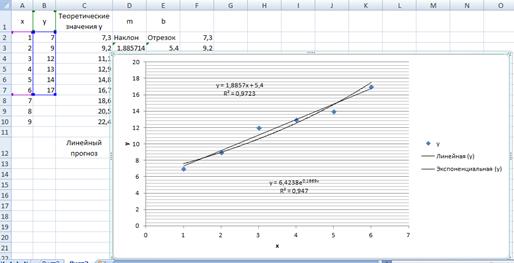
Рис. 7.21.






