| Число степеней свободы f 1 | |||||||
| Значение коэффициента | 12.71 | 4.30 | 3.18 | 2.78 | 2.57 | 2.45 | 2.36 |
Если коэффициент не удовлетворяет критерию Стьюдента, то он считается незначимым и приравнивается к нулю.
Проверка адекватности (соответствия) полученного уравнения регрессии экспериментальным данным проводится с помощью критерия Фишера. Для этого вычисляются
 , F =
, F = 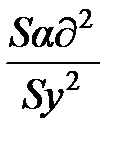 ,
,
где  – оценка дисперсии адекватности; B – число значимых коэффициентов уравнения регрессии; yэj, ypj – экспериментальное и рассчитанное по найденной математической модели значения y в j -м опыте.
– оценка дисперсии адекватности; B – число значимых коэффициентов уравнения регрессии; yэj, ypj – экспериментальное и рассчитанное по найденной математической модели значения y в j -м опыте.
Определяется также табличное значение критерия Фишера FТ из табл. 21.2 по числу степеней свободы f 1 и числу степеней свободы f 2 = N – B.
Если F < FТ, то уравнение регрессии рассматривается как модель исследуемого процесса.
Таблица 21.2
Коэффициенты критерия Фишера
| Число степеней свободы f 1 | Число степеней свободы f 2 | |||||
| 161.40 | 199.50 | 215.70 | 224.60 | 320.20 | 234.00 | |
| 18.51 | 19.00 | 19.16 | 19.25 | 19.30 | 19.33 | |
| 10.13 | 9.55 | 9.28 | 9.12 | 9.01 | 8.94 | |
| 7.71 | 6.94 | 6.59 | 6.39 | 6.26 | 6.16 | |
| 6.61 | 5.79 | 5.41 | 5.19 | 5.05 | 4.95 | |
| 5.99 | 5.14 | 4.76 | 4.53 | 3.39 | 4.28 | |
| 5.99 | 4.74 | 4.35 | 4.12 | 3.97 | 3.97 |
Если полученное уравнение не адекватно процессу, то нужно перейти к более сложному виду математической модели, вновь провести опыты и обработать их результаты.
Если уравнение адекватно процессу, то нужно от кодированных переменных перейти к физическим.
Задание для выполнения на компьютере
1. В табл. 21.3 приведены значения входных и выходных параметров некоторого процесса. В качестве эмпирической формулы выбрать полином второй степени и составить программу получения его коэффициентов. Номер варианта определяет преподаватель.
2. Определить коэффициенты математической модели процесса в виде полинома второй степени с помощью приложений Mathcad и Excel. Результаты сравнить между собой.
Таблица 21.3
Исходные данные для расчета
| № п/п | Переменные | Значения переменных | ||||||||
| x | 2.1 | 2.7 | 3.3 | 3.8 | 4.2 | 4.9 | 5.6 | 6.1 | 6.8 | |
| y | 1.2 | 1.6 | 2.1 | 2.4 | 2.5 | 2.8 | 3.4 | 3.8 | 4.0 | |
| x | 0.2 | 0.7 | 1.1 | 1.6 | 2.2 | 2.3 | 3.0 | 3.9 | 4.3 | |
| y | 6.3 | 10.6 | 14.2 | 15.7 | 15.9 | 15.5 | 12.5 | 5.0 | 0.2 | |
| x | –5.0 | –4.2 | –3.5 | –2.8 | –1.9 | –1.2 | –0.3 | 0.8 | 1.3 | |
| y | 8.8 | 4.3 | 1.8 | –0.2 | –0.8 | –0.5 | 1.8 | 7.6 | 12.2 | |
| x | 0.0 | 0.6 | 1.3 | 1.8 | 2.7 | 3.1 | 3.9 | 4.2 | 5.1 | |
| y | 10.2 | 8.2 | 6.0 | 5.1 | 1.5 | 0.8 | –1.6 | –2.8 | –5.5 | |
| x | –0.4 | –3.5 | –2.4 | –2.0 | –0.8 | 0.5 | 1.4 | 2.5 | 3.8 | |
| y | –1.6 | –1.4 | –1.1 | –0.9 | –0.7 | –0.5 | –0.4 | –0.2 | 0.1 | |
| x | 3.1 | 3.7 | 4.3 | 4.8 | 5.2 | 5.9 | 6.6 | 7.1 | 7.8 | |
| y | 1.2 | 1.6 | 2.1 | 2.4 | 2.5 | 2.8 | 3.4 | 3.8 | 4.0 | |
| x | 0.2 | 0.7 | 1.1 | 1.6 | 2.2 | 2.3 | 3.0 | 3.9 | 4.7 | |
| y | 6.3 | 9.6 | 13.2 | 14.7 | 14.9 | 14.5 | 11.5 | 4.0 | 2.1 | |
| x | –3.0 | –2.2 | –1.5 | –1.1 | –0.9 | –0.2 | 0.3 | 0.8 | 1.3 | |
| y | 8.8 | 4.3 | 1.8 | –0.2 | –0.8 | –0.5 | 1.8 | 7.6 | 12.2 | |
| x | 0.0 | 0.6 | 1.3 | 1.8 | 2.7 | 3.1 | 3.9 | 4.2 | 5.1 | |
| y | 12.2 | 9.2 | 8.0 | 7.1 | 0.5 | 0.8 | –2.6 | –3.8 | –6.5 | |
| x | –5.4 | –3.5 | –2.4 | –2.0 | –0.8 | 0.5 | 1.4 | 2.5 | 3.4 | |
| y | –1.6 | –1.1 | –0.8 | –0.7 | 0.7 | 1.4 | 2.1 | 3.2 | 3.9 | |
| x | 4.1 | 5.7 | 6.3 | 6.8 | 7.2 | 7.9 | 8.6 | 9.1 | 9.8 | |
| y | 1.2 | 1.6 | 2.1 | 2.4 | 2.5 | 2.8 | 3.4 | 3.8 | 4.0 | |
| x | 0.2 | 0.7 | 1.1 | 1.6 | 2.2 | 2.3 | 3.0 | 3.9 | 4.3 | |
| y | 7.3 | 11.6 | 16.2 | 17.7 | 17.9 | 15.5 | 12.5 | 5.0 | 0.2 | |
| x | –3.0 | –2.2 | –1.5 | –0.8 | 0.2 | 0.3 | 1.3 | 1.8 | 2.3 | |
| y | 8.8 | 4.3 | 1.8 | –0.2 | –0.8 | –0.5 | 1.8 | 7.6 | 12.2 | |
| x | 0.0 | 0.6 | 1.3 | 1.8 | 2.7 | 3.1 | 3.9 | 4.2 | 5.1 | |
| y | 20.2 | 28.2 | 26.0 | 25.1 | 21.5 | 20.8 | 11.6 | 12.8 | 15.5 | |
| x | 0.4 | 1.5 | 2.4 | 2.8 | 3.1 | 4.5 | 5.4 | 5.5 | 6.8 | |
| y | –1.6 | –1.3 | –1.0 | –0.8 | –0.7 | –0.4 | –0.2 | –0.2 | 0.3 |
МЕТОДЫ ОПТИМИЗАЦИИ
Задачу оптимизации в общем виде можно сформулировать так: определить значения входных параметров x 1, x 2, …, xn некоторого процесса, которые обеспечивают максимум или минимум целевой функции f (x 1, x 2, …, xn), характеризующей показатели процесса, и удовлетворяют ограничениям, если они присутствуют.
Метод сканирования
Рассмотрим использование метода сканирования на примере для оптимизации процесса, имеющего два входных параметра x1, x2 и выходной параметр – y. Пусть требуется определить оптимальные значения x 1 и x 2, которые обеспечивали бы минимум целевой функции
y = f (x 1, x 2)
и удовлетворяли ограничениям:
a 1 <= x 1 <= b 1, a 2 <= x 2 <= b 2
g (x 1, x 2) > 0
(последнее ограничение может отсутствовать).
Метод сканирования заключается в нахождении значений x 1 из интервала [ a 1, b 1], начиная с a 1 и до b 1 с шагом h 1 и определении значений x 2 из интервала [ a 2, b 2], начиная с a 2 и до b 2 с шагом h 2. Для всех значений x 1 и x 2, удовлетворяющих ограничениям g (x 1, x 2) > 0, нужно вычислить значения целевой функции y = f (x 1, x 2).
Те значения x1 и x2, для которых значение целевой функции минимально, являются искомым решением.
Рассмотрим алгоритм метода сканирования:
1. Ввод исходных данных: a 1, b 1, h 1, a 2, b 2, h 2 инекоторого числа A, заведомо большего, чем значение целевой функции.
2. Вычисление yopt = A, x 1 opt = a 1, x 2 opt = a 2.
3. x 1 = a 1
4. x 2 = a 2
5. Проверка ограничения: если ограничение не выполняется, т. е. g (x 1, x 2) <= 0, то переход к п. 8, иначе – переход к следующему пункту.
6. Вычисление целевой функции y = f (x 1, x 2).
7. Если y < yopt, то yopt = y, x 1 opt = x 1, x 2 opt = x 2, иначе – переход к следующему пункту.
8. Вычисление x 2 = x 2 + h 2.
9. Если x 2 <= b 2, то переход к п. 5, иначе – переход к следующему пункту.
10. Вычисление x 1 = x 1 + h 1.
11. Если x 1 <= b 1, то переход к п. 4, иначе – переход к следующему пункту.
12. Вывод оптимальных значений x 1 opt, x 2 opt и минимального значения целевой функции yopt.
Метод случайного поиска
Рассмотрим применение метода случайного поиска для оптимизации процесса на примере, приведенном выше. Идея метода основана на многократном (N раз) вычислении целевой функции y для значений x 1 и x 2, выбранных из отрезков [ a 1, b 1] и [ a 2, b 2] случайным образом. Те значения x 1 и x 2, при которых целевая функция минимальна и удовлетворяются ограничения и являются решением.
Для определения случайного числа x на отрезке [ a, b ] можно использовать встроенную функцию Rnd. Тогда x = (b – a) × Rnd (1) + a.
Алгоритм метода случайного поиска:
1. Ввод исходных данных: a 1, b 1, a 2, b 2,количества опытов N ичисла A, заведомо большего, чем значение целевой функции.
2. Вычисление yopt = A, x 1 opt = a 1, x 2 opt = a 2.
3. i = 1.
4. Вычисление x 1 = (b 1 – a 1) × Rnd (1) + a 1, x 2 = (b 2 – a2) × Rnd (1) + + a 2.
5. Проверка ограничения: если g (x 1, x 2) <= 0, то переход к п. 8, иначе – переход к следующему пункту.
6. Вычисление целевой функции y = f (x 1, x 2).
7. Если y < yopt,то yopt = y, x 1 opt = x 1, x 2 opt = x 2, иначе – переход к следующему пункту.
8. i = i + 1.
9. Если i <= N, то переход к п. 4, иначе – переход к п. 10.
10. Вывод оптимальных значений x 1 opt, x 2 opt и минимального значения целевой функции yopt.




