Системи координат
Робота
Студента групи ФІ-09
Бушуєв Станіслав Андрійович
Кривий Ріг 2013
Формули сферичної геометрії. Паралактичний трикутник. Перетворення небесних координат.
Сферична геометрія — розділ геометрії, який вивчає геометричні фігури на поверхні сфери. Це приклад неевклідової геометрії. Сферична геометрія виникла в давнину в зв'язку з потребами географії та астрономії.
При перетині двох великих кіл утворюються чотири сферичні двокутники. Площа двокутника визначається формулою 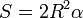 , де
, де 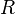 — радіус сфери, а
— радіус сфери, а 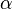 — кут двокутника.
— кут двокутника.
Сторони сферичного трикутника вимірюють величиною кута, утвореного радіусами сфери, проведеними до кінців цієї сторони. Кожна сторона сферичного трикутника менша суми і більша різниці двох інших. Сума всіх сторін сферичного трикутника завжди менша 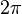 . Сума кутів сферичного трикутника
. Сума кутів сферичного трикутника  завжди більша
завжди більша 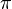 і менша
і менша 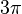 . Величина
. Величина 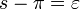 називається сферичним надлишком. Площа сферичного трикутника визначається за формулою Жирара
називається сферичним надлишком. Площа сферичного трикутника визначається за формулою Жирара 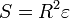 .
.
Сфери́чні гармо́ніки — набір ортонормованих функцій двох кутових змінних 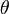 і
і 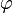 , які складають повний базис функцій сферичного кута.
, які складають повний базис функцій сферичного кута.
Сферичні гармоніки позначаються 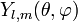 , де l = 0,1,2…, а m пробігає значення від -l до l.
, де l = 0,1,2…, а m пробігає значення від -l до l.
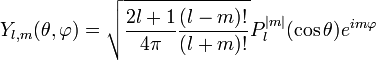 ,
,
де 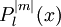 - приєднані поліноми Лежандра.
- приєднані поліноми Лежандра.
Сферичні гармоніки є власними функціями оператора кутового моменту.
Множник в означенні сферичних гармонік вибирається з умови нормування
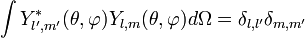 ,
,
де інтегрування проводиться по повному сферичному куту, а 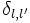 - символ Кронекера.
- символ Кронекера.
| Паралактичний трикутник | 
|
Сферичні трикутники, розміщені на небесній сфері, називаються астрономічними.
Перший астрономічний або паралактичний трикутник
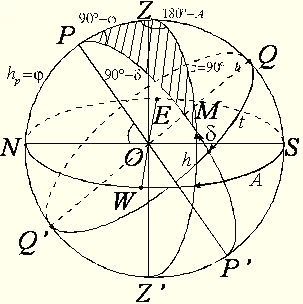 Трикутник, розміщений на небесній сфері і містить у вершинах зеніт Z, полюс світу P і будь-яке світило М, а сторони якого зображаються дугами небесного меридіана, кола висоти світила і кола схилення світила називають паралактичним або першим астрономічним трикутником.
Сторони цього трикутника: PZ=90о–φ (φ – широта місця спостереження), ZM=z=90о–h (z – зенітна віддаль світила), PM=90о–δ (δ – схилення світила).
Кути цього трикутника: PZM=180о–А (А – азимут світила), ZPM=t (t – годинний кут світила), PMZ – з астрономічними координатами не зв’язаний і не має спеціального позначення.
Другий астрономічний трикутник Трикутник, розміщений на небесній сфері і містить у вершинах зеніт Z, полюс світу P і будь-яке світило М, а сторони якого зображаються дугами небесного меридіана, кола висоти світила і кола схилення світила називають паралактичним або першим астрономічним трикутником.
Сторони цього трикутника: PZ=90о–φ (φ – широта місця спостереження), ZM=z=90о–h (z – зенітна віддаль світила), PM=90о–δ (δ – схилення світила).
Кути цього трикутника: PZM=180о–А (А – азимут світила), ZPM=t (t – годинний кут світила), PMZ – з астрономічними координатами не зв’язаний і не має спеціального позначення.
Другий астрономічний трикутник
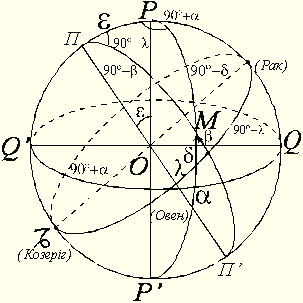 Трикутник, розміщений на небесній сфері і містить у вершинах полюс світу P, полюс екліптики П і будь-яке світило М, а сторони якого зображаються дугами кола схилення, кола широти світила і кола широти, що проходить через полюс світу, називається другим астрономічним трикутником.
Сторони трикутника: PM=90о–δ, ПМ=90о–β (β – широта світила), ПР=ε (ε – кут нахилу екліптики до екватора).
Кутитрикутника: РПМ=90о–λ (λ – довгота світила), ПРМ=90о+α (α – пряме сходження світила), ПМР – з астрономічними координатами не зв’язаний.
Трикутник, розміщений на небесній сфері і містить у вершинах полюс світу P, полюс екліптики П і будь-яке світило М, а сторони якого зображаються дугами кола схилення, кола широти світила і кола широти, що проходить через полюс світу, називається другим астрономічним трикутником.
Сторони трикутника: PM=90о–δ, ПМ=90о–β (β – широта світила), ПР=ε (ε – кут нахилу екліптики до екватора).
Кутитрикутника: РПМ=90о–λ (λ – довгота світила), ПРМ=90о+α (α – пряме сходження світила), ПМР – з астрономічними координатами не зв’язаний.
|
| Перетворення небесних координат | 
|
Перехід від горизонтальних координат до перших екваторіальних
Нехай в заданому місці, широта φ якого відома із спостережень, визначені горизонтальні координати світила М: зенітна віддаль z і азимут А. Визначити координати світила М в першій екваторіальній системі координат. Побудуємо для цього паралактичний трикутник. До сторони РМ застосуємо теорему косинусів:
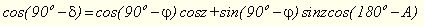 ,
або ,
або 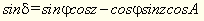 (1).
У (1) φ, z, А - задані, а тому можна визначити схилення світила δ. До сторін ZМ і РМ застосуємо теорему синусів: (1).
У (1) φ, z, А - задані, а тому можна визначити схилення світила δ. До сторін ZМ і РМ застосуємо теорему синусів:
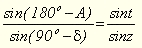 знаходимо sin t:
знаходимо sin t: 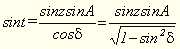 (2).
У (2) А, z задані, а δ визначається з (1), тому визначаємо годинний кут t.
Обернена задача: нехай задані координати δ і t світила М і відома широта φ місця спостереження. Визначити горизонтальні координати z і А. За теоремою косинусів до сторони ZM: (2).
У (2) А, z задані, а δ визначається з (1), тому визначаємо годинний кут t.
Обернена задача: нехай задані координати δ і t світила М і відома широта φ місця спостереження. Визначити горизонтальні координати z і А. За теоремою косинусів до сторони ZM:
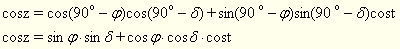 (3).
У (3) φ, δ, t задано, а тому визначаємо зенітну віддаль світила. Застосуємо теорему синусів до сторін МZ і РМ: (3).
У (3) φ, δ, t задано, а тому визначаємо зенітну віддаль світила. Застосуємо теорему синусів до сторін МZ і РМ: 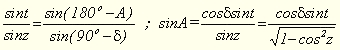 (4).
Так як δ і t задані, а z визначається за формулою (3), то (4) визначає азимут світила М.
Перехід від першої екваторіальної системи координат до другої
Нехай задано координати t і δ світила М в першій екваторіальній системі координат. Так як координата t світила М міняється в результаті добового обертання небесної сфери, то необхідно задати час до якого відносяться ці координати. Цей час може бути задано в будь-якій системі виміру: зоряний, поясний, середній сонячний. Припустимо, що відомо зоряний час s, тоді (4).
Так як δ і t задані, а z визначається за формулою (3), то (4) визначає азимут світила М.
Перехід від першої екваторіальної системи координат до другої
Нехай задано координати t і δ світила М в першій екваторіальній системі координат. Так як координата t світила М міняється в результаті добового обертання небесної сфери, то необхідно задати час до якого відносяться ці координати. Цей час може бути задано в будь-якій системі виміру: зоряний, поясний, середній сонячний. Припустимо, що відомо зоряний час s, тоді
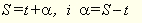 (5).
Ця формула дозволяє перейти від першої екваторіальної системи координат до другої екваторіальної системи координат, а друга координата схилення в обох системах однакова.
Перехід від другої екваторіальної системи координат до екліптичної системи координат
Нехай відомо координати α і δ світила М в другій екваторіальній системі координат. Визначимо координати λ і β світила М в екліптичній системі координат. Для світила М будуємо другий астрономічний трикутник. Застосуємо теорему косинусів до сторони ПМ: (5).
Ця формула дозволяє перейти від першої екваторіальної системи координат до другої екваторіальної системи координат, а друга координата схилення в обох системах однакова.
Перехід від другої екваторіальної системи координат до екліптичної системи координат
Нехай відомо координати α і δ світила М в другій екваторіальній системі координат. Визначимо координати λ і β світила М в екліптичній системі координат. Для світила М будуємо другий астрономічний трикутник. Застосуємо теорему косинусів до сторони ПМ:
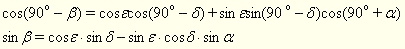 (6).
δ, α, ε – відомі, тому формула (6) визначає широту β світила М.
Застосуємо теорему синусів до сторін ПМ, РМ: (6).
δ, α, ε – відомі, тому формула (6) визначає широту β світила М.
Застосуємо теорему синусів до сторін ПМ, РМ:
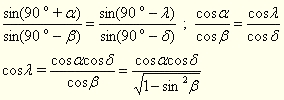 (7).
α, δ – відомі, а β визначається з (6), тому (7) дозволяє визначити довготу λ точки М.
Обернена задача: дано екліптичні координати β, λ світила М.
Визначити екваторіальні координати α, δ. Застосуємо теорему косинусів до сторони РМ: (7).
α, δ – відомі, а β визначається з (6), тому (7) дозволяє визначити довготу λ точки М.
Обернена задача: дано екліптичні координати β, λ світила М.
Визначити екваторіальні координати α, δ. Застосуємо теорему косинусів до сторони РМ:
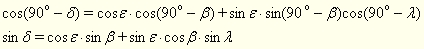 (8).
Застосуємо теорему синусів до сторін РМ і ПМ: (8).
Застосуємо теорему синусів до сторін РМ і ПМ:
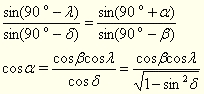 (9)
ε, β, λ – відомі, тому з (8) визначаємо δ. За відомими β, λ, δ визначаємо α з формули (9). (9)
ε, β, λ – відомі, тому з (8) визначаємо δ. За відомими β, λ, δ визначаємо α з формули (9).
|






