До сих пор в качестве факторов рассматривались экономические переменные, принимающие количественные значения в некотором интервале. Вместе с тем может оказаться необходимым включить в модель фактор, имеющий два или более качественных уровней. Это могут быть разного рода атрибутивные признаки, такие, например, как профессия, пол, образование, климатические условия, принадлежность к определенному региону. Чтобы ввести такие переменные в регрессионную модель, им должны быть присвоены те или иные цифровые метки, т.е. качественные переменные преобразованы в количественные. Такого вида сконструированные переменные в эконометрике принято называть фиктивными переменными.
Рассмотрим применение фиктивных переменных для функции спроса. Предположим, что по группе лиц мужского и женского пола изучается линейная зависимость потребления кофе от цены. В общем виде уравнение регрессии имеет вид:
 ,
,
где y – количество потребляемого кофе; x – цена.
Аналогичные уравнения могут быть найдены отдельно для лиц мужского пола:  и женского пола:
и женского пола:  .
.
Различия в потреблении кофе проявятся в различии средних 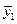 и
и  . Вместе с тем сила влияния x на y может быть одинаковой, т.е.
. Вместе с тем сила влияния x на y может быть одинаковой, т.е.  . В этом случае возможно построение общего уравнения регрессии с включением в него фактора «пол» в виде фиктивной переменной. Объединяя уравнения
. В этом случае возможно построение общего уравнения регрессии с включением в него фактора «пол» в виде фиктивной переменной. Объединяя уравнения  и
и  и, вводя фиктивные переменные, можно прийти к следующему выражению:
и, вводя фиктивные переменные, можно прийти к следующему выражению:
 ,
,
где  и
и  – фиктивные переменные, принимающие значения:
– фиктивные переменные, принимающие значения:


В общем уравнении регрессии зависимая переменная y рассматривается как функция не только цены x, но и пола  . Переменная z рассматривается как дихотомическая переменная, принимающая всего два значения: 1 и 0. При этом когда
. Переменная z рассматривается как дихотомическая переменная, принимающая всего два значения: 1 и 0. При этом когда  , то
, то  , и наоборот.
, и наоборот.
Для лиц мужского пола, когда  и
и  , объединенное уравнение регрессии составит:
, объединенное уравнение регрессии составит:  , а для лиц женского пола, когда
, а для лиц женского пола, когда  и
и  :
:  . Иными словами, различия в потреблении для лиц мужского и женского пола вызваны различиями свободных членов уравнения регрессии:
. Иными словами, различия в потреблении для лиц мужского и женского пола вызваны различиями свободных членов уравнения регрессии:  . Параметр b является общим для всей совокупности лиц, как для мужчин, так и для женщин.
. Параметр b является общим для всей совокупности лиц, как для мужчин, так и для женщин.
Однако при введении двух фиктивных переменных  и
и  в модель
в модель  применение МНК для оценивания параметров
применение МНК для оценивания параметров 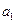 и
и  приведет к вырожденной матрице исходных данных, а, следовательно, и к невозможности получения их оценок. Объясняется это тем, что при использовании МНК в данном уравнении появляется свободный член, т.е. уравнение примет вид
приведет к вырожденной матрице исходных данных, а, следовательно, и к невозможности получения их оценок. Объясняется это тем, что при использовании МНК в данном уравнении появляется свободный член, т.е. уравнение примет вид
 .
.
Предполагая при параметре A независимую переменную, равную 1, имеем следующую матрицу исходных данных:
 .
.
В рассматриваемой матрице существует линейная зависимость между первым, вторым и третьим столбцами: первый равен сумме второго и третьего столбцов. Поэтому матрица исходных факторов вырождена. Выходом из создавшегося затруднения может явиться переход к уравнениям

или
 ,
,
т.е. каждое уравнение включает только одну фиктивную переменную  или
или  .
.
Предположим, что определено уравнение
 ,
,
где  принимает значения 1 для мужчин и 0 для женщин.
принимает значения 1 для мужчин и 0 для женщин.
Теоретические значения размера потребления кофе для мужчин будут получены из уравнения
 .
.
Для женщин соответствующие значения получим из уравнения
 .
.
Сопоставляя эти результаты, видим, что различия в уровне потребления мужчин и женщин состоят в различии свободных членов данных уравнений: A – для женщин и 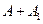 – для мужчин.
– для мужчин.
Теперь качественный фактор принимает только два состояния, которым соответствуют значения 1 и 0. Если же число градаций качественного признака-фактора превышает два, то в модель вводится несколько фиктивных переменных, число которых должно быть меньше числа качественных градаций. Только при соблюдении этого положения матрица исходных фиктивных переменных не будет линейно зависима и возможна оценка параметров модели.
Пример. Проанализируем зависимость цены двухкомнатной квартиры от ее полезной площади. При этом в модель могут быть введены фиктивные переменные, отражающие тип дома: «хрущевка», панельный, кирпичный.
При использовании трех категорий домов вводятся две фиктивные переменные:  и
и  . Пусть переменная
. Пусть переменная  принимает значение 1 для панельного дома и 0 для всех остальных типов домов; переменная
принимает значение 1 для панельного дома и 0 для всех остальных типов домов; переменная  принимает значение 1 для кирпичных домов и 0 для остальных; тогда переменные
принимает значение 1 для кирпичных домов и 0 для остальных; тогда переменные  и
и  принимают значения 0 для домов типа «хрущевки».
принимают значения 0 для домов типа «хрущевки».
Предположим, что уравнение регрессии с фиктивными переменными составило:
 .
.
Частные уравнения регрессии для отдельных типов домов, свидетельствуя о наиболее высоких ценах квартир в панельных домах, будут иметь следующий вид: «хрущевки» –  ; панельные –
; панельные –  ; кирпичные –
; кирпичные –  .
.
Параметры при фиктивных переменных  и
и  представляют собой разность между средним уровнем результирующего показателя для соответствующей группы и базовой группы. В рассматриваемом примере за базу сравнения цены взяты дома «хрущевки», для которых
представляют собой разность между средним уровнем результирующего показателя для соответствующей группы и базовой группы. В рассматриваемом примере за базу сравнения цены взяты дома «хрущевки», для которых  . Параметр при
. Параметр при  , равный 2200, означает, что при одной и той же полезной площади квартиры цена ее в панельных домах в среднем на 2200 долл. США выше, чем в «хрущевках». Соответственно параметр при
, равный 2200, означает, что при одной и той же полезной площади квартиры цена ее в панельных домах в среднем на 2200 долл. США выше, чем в «хрущевках». Соответственно параметр при  показывает, что в кирпичных домах цена выше в среднем на 1600 долл. при неизменной величине полезной площади по сравнению с указанным типом домов.
показывает, что в кирпичных домах цена выше в среднем на 1600 долл. при неизменной величине полезной площади по сравнению с указанным типом домов.
В отдельных случаях может оказаться необходимым введение двух и более групп фиктивных переменных, т.е. двух и более качественных факторов, каждый из которых может иметь несколько градаций. Например, при изучении потребления некоторого товара наряду с факторами, имеющими количественное выражение (цена, доход на одного члена семьи, цена на взаимозаменяемые товары и др.), учитываются и качественные факторы. С их помощью оцениваются различия в потреблении отдельных социальных групп населения, дифференциация в потреблении по полу, национальному составу и др. При построении такой модели из каждой группы фиктивных переменных следует исключить по одной переменной. Так, если модель будет включать три социальные группы, три возрастные категории и ряд экономических переменных, то она примет вид:
 ,
,
где y – потребление;


 – экономические (количественные) переменные.
– экономические (количественные) переменные.
До сих пор мы рассматривали фиктивные переменные как факторы, которые используются в регрессионной модели наряду с количественными переменными. Вместе с тем возможна регрессия только на фиктивных переменных. Например, изучается дифференциация заработной платы рабочих высокой квалификации по регионам страны. Модель заработной платы может иметь вид:
 ,
,
где y – средняя заработная плата рабочих высокой квалификации по отдельным предприятиям;


………………………………………………………………………..

Поскольку последний район, указанный в модели, обозначен  , то в исследование включено
, то в исследование включено 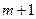 район.
район.




