Множества. Операции над множествами. Числовые множества

И.Э. Гриншпон, Я.С. Гриншпон

 

 

ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ И ИХ ГРАФИКИ

 

Учебное пособие

 

Томск

Издательство Томского государственного университета

систем управления и радиоэлектроники

 

Гриншпон И.Э., Гриншпон Я.С.

Элементарные функции и их графики: учеб. пособие / И.Э. Гриншпон, Я.С. Гриншпон. – Томск: Изд-во Томск. гос. ун-та систем упр. и радиоэлектроники, 2011. – 52 с.

 

Приведены определения, свойства и графики основных элементарных функций, а также правила линейных преобразований графиков функций. Особое внимание уделено графикам гармонических колебаний.

 

 

Учебное издание

Гриншпон Ирина Эдуардовна

Гриншпон Яков Самуилович

ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ

И ИХ ГРАФИКИ

 

Учебное пособие

Компьютерная верстка Я.С. Гриншпона

Подписано в печать... Формат 60´84/16.

Усл. печ. л. …... Заказ. Тираж экз.

Томский государственный университет

систем управления и радиоэлектроники.

634050, г. Томск, пр. Ленина, 40.

Тел. 8 (3822) 533018.

 

Ó	Гриншпон И.Э., Гриншпон Я.С., 2011
Ó	Изд-во Томск. гос. ун-та систем упр. и радиоэлектроники, 2011

 

Введение

При изучении различных явлений мы обычно имеем дело с совокупностью переменных величин, связанных между собой так, что значения одних переменных величин (независимых переменных) определяют значения других переменных величин (зависимых переменных или функций). Например, при изменении радиуса круга меняется его площадь. При изменении скорости тела изменяется путь, пройденный телом за данный промежуток времени. При изменении сопротивления проводника изменяется сила тока в цепи.

Отвлекаясь от конкретного смысла переменных, математика рассматривает абстрактные переменные величины, изучает их взаимосвязи.

Понятие переменой величины (функции) является одним из центральных понятий математического анализа. Оно является для математики и ее приложений, связанных с изучением переменных величин, таким же фундаментальным, как понятие числа для арифметики.

Как и остальные понятия математики, понятие функции сложилось не сразу, а прошло долгий путь развития.

Впервые понятие функции было введено в знаменитом труде математика и философа Рене Декарта «Геометрия» (1637 г.) под названием «переменная величина». В геометрическом и механическом понимании это понятие интерпретируется у Исаака Ньютона (1671 г.). Под функцией он понимал переменную величину, которая изменяется с течением времени. Эту величину Ньютон называл «флюентой».

Термин «функция» (от латинского functio – исполнение) впервые ввёл в 1673 году немецкий математик Готфрид Лейбниц в письме к Гюйгенсу. У Лейбница функция связывалась с геометрическим образом (под функцией он понимал отрезок, длина которого меняется по какому-нибудь определенному закону). В работах Декарта, Ферма, Ньютона и Лейбница понятие функции носило по существу интуитивный характер и было связано либо с геометрическими, либо с механическими представлениями. В 18 веке функцию стали рассматривать как формулу, связывающую одну переменную с другой. Швейцарский математик Иоганн Бернулли в 1718 году определил функцию следующим образом: «функцией переменной величины называют количество, образованное каким угодно способом из этой переменной величины и постоянных». В 1755 году в «Дифференциальном исчислении» Леонард Эйлер дает общее определение функции: «Когда некоторые количества зависят друг от друга таким образом, что при изменении последних и сами они подвергаются изменению, то первые называют функцией вторых».

Современное определение функции как зависимости одной переменной величины от другой было дано в работах Николая Ивановича Лобачевского («Об изчезании тригонометрических строк», 1834 г.) и чешского математика Бернарда Больцано.

Введение переменной в математику оказало решающее влияние на развитие математической науки. Кроме количественных соотношений между постоянными величинами, математика смогла изучать процессы, связанные с изменением величин и движением вообще.

Среди всего многообразия функций исторически выделились функции, отличающиеся своей простотой и наиболее широкой областью применения. Это простейшие элементарные функции, основное значение которых состоит в том, что они составляют базу для изучения более сложных функций, являясь в большинстве своем составными элементами последних. К элементарным функциям относятся основные элементарные функции (степенные, тригонометрические, обратные тригонометрические, показательные, логарифмические) и те, которые можно образовать из них с помощью конечного числа операций (сложения, вычитания, умножения, деления) и суперпозиций.

Для успешного усвоения программы по высшей математике студент должен иметь достаточную математическую базу. В этом пособии систематизированы сведения о функциях, которые изучались в школе на протяжении всего курса математики. В нем рассматриваются основные элементарные функции, приводятся их свойства, строятся графики. Излагается построение графиков линейной, квадратичной и дробно-линейной функций. Рассматриваются линейные преобразования графиков функций: параллельный перенос графиков, их сжатие и растяжение по осям, симметрии относительно осей координат. В последнем параграфе рассматриваются гармонические колебания и строятся графики гармоник.

Рассмотрение элементарных функций продиктовано необходимостью повторения и закрепления знаний студентов по данному разделу математики и подготовки их к успешному изучению математического анализа.

Множества. Операции над множествами. Числовые множества

Множество – одно из основных понятий современной математики. Это понятие не сводится к другим понятиям и не определяется. Объекты, составляющие множество, называют его элементами. Множества обозначают заглавными латинскими буквами: A, B, C, X, …, их элементы – прописными буквами: a, b, c, x, … или буквами с индексами a ₁, a ₂, a ₃,... Множество, не содержащее ни одного элемента, называют пустым и обозначают Æ.

Чтобы задать множество, необходимо знать, какие объекты принадлежат множеству, а какие нет. Если множество содержит немного элементов, то его можно задать, перечислив все его элементы. Если множество задано списком, то его элементы записывают в фигурных скобках через точку с запятой. Множество цифр можно записать следующим образом: A = {1; 2; 3; 4; 5; 6; 7; 8; 9; 0}; множество простых чисел, меньших 20, – B = {2; 3; 5; 7; 11; 13; 17; 19}; множество дней недели – С = {понедельник; вторник; среда; четверг; пятница; суббота; воскресенье}.

Однако задать множество списком можно только тогда, когда оно содержит конечное число элементов (но и это неудобно, если число элементов множества велико). Существует универсальный способ задания множеств. Множество может быть задано с помощью характеристического свойства, то есть такого свойства, которым обладают все элементы множества, и не обладают объекты, не принадлежащие множеству. Задание множества с помощью характеристического свойства записывают следующим образом: А = { х | P (х)}, где P (x) – характеристическое свойство.

Приведем несколько примеров:

1. Если , то .

2. Пусть B – множество остатков от деления натуральных чисел на 7. Тогда .

3. Если D – множество действительных чисел, не меньших двух и не больших семи, то D – отрезок [2; 7].

Рассмотрим два множества A и B. Если каждый элемент множества B является элементом множества A, то говорят, что B – подмножество множества A. Этот факт записывают так: В Ì А. Считают, что пустое множество является подмножеством любого множества. Каждое непустое множество А имеет хотя бы два подмножества – само множество А и пустое множество.

Пусть даны два множества А и В.

Пересечением (произведением) множеств А и В называется множество, состоящее из всех элементов, принадлежащих одновременно и множеству А, и множеству В. Обозначают пересечение множеств A Ç B:

A Ç B = { х | х Î A и х Î B }.

Объединением (суммой) множеств А и В называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из множеств А или В. Обозначают объединение множеств A È B:

A È B = { х | х Î A или х Î B }.

Разностью множеств А и В называется множество, состоящее из всех элементов множества А, не принадлежащих множеству В. Обозначают разность множеств A \ B:

A \ B = { х | х Î A и х Ï B }.

Элементами множества могут быть различные объекты – числа, слова, геометрические фигуры, функции и т. д. В математике особую роль играют числовые множества, то есть множества, элементами которых являются числа.

Например: ¥ – множество натуральных чисел, ¢ – множество целых чисел, ¤ – множество рациональных чисел, ¡ – множество действительных чисел.

Напомним, что натуральными называют числа, используемые при счете предметов, то есть . Целыми считают натуральные числа, противоположные им отрицательные числа и число ноль. Таким образом, 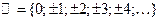. Рациональные числа – это обыкновенные дроби с целым числителем и натуральным знаменателем: 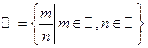. Любое рациональное число может быть записано в виде конечной или бесконечной периодической десятичной дроби.

Все десятичные дроби (в том числе и бесконечные непериодические) образуют множество действительных чисел. Действительные числа изображают точками на координатной прямой (числовой оси). Точка О, соответствующая числу 0, разбивает координатную прямую на два луча: положительный и отрицательный. Число, изображением которого на координатной прямой является точка М, называется координатой точки М. Если , то точка с координатой лежит левее точки с координатой .

Особое значение в математике имеют подмножества множества ¡, называемые числовыми промежутками: отрезок [ a; b ] – множество точек х, удовлетворяющих условию ; интервал (a; b) – множество точек х, удовлетворяющих условию ; полуинтервалы [ a; b) и (a; b ] – множества точек х, удовлетворяющих условиям и 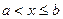соответственно; бесконечные промежутки (a; +¥), (– ¥; b), [ a; +¥), (–¥; b ] – множества точек х, удовлетворяющих условиям , , , соответственно.

Множество точек числовой прямой, удовлетворяющих условию , называется окрестностью точки а радиуса r. Окрестность можно записать также через двойное неравенство или неравенство с модулем .

Понятие функции

Пусть Х и Y – некоторые числовые множества и пусть указано правило, по которому каждому элементу х множества Х поставлено в соответствие единственное значение у из множества Y. Это соответствие называется функцией и обозначается . Переменная х называется независимой или аргументом, переменная у – зависимой или функцией. Множество Х называется областью определения функции и обозначается D (f). Множество Y (множество всех значений, которые принимает переменная у) называется областью изменения (областью значений) функции и обозначается E (f).

Две функции называются равными, если они имеют одинаковые области определения и каждому значению аргумента они ставят в соответствие одно и тоже число.

Наиболее распространенный способ задания функции – аналитический, то есть с помощью формулы. Например, функцию, ставящую в соответствие каждому неотрицательному числу х его квадратный корень, можно записать в виде или . Этот способ задания функции компактен, содержит полную информацию о свойствах функции и наиболее удобен при проведении расчетов. Если не сделано специальной оговорки, то за область определения функции берут все значения аргумента, для которых указанные в формуле действия выполнимы. 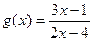Например, область определения функции все неотрицательные значения х, то есть , а для функции – область определения все действительные значения х, кроме , то есть D (g) = ¡\{2}.

Иногда для разных значений х функция задается разными формулами. В этом случае используют обозначение: , причем . График такой функции состоит из n частей.

На практике часто используют табличный способ задания функции. При этом способе задания функции приводится таблица, в которой для имеющихся значений аргумента указываются соответствующие значения функции. Табличный способ важен потому, что он является основным при описании реальных зависимостей, возникающих при проведении различных экспериментов. С математической точки зрения табличное задание функции неполно, так как оно позволяет найти значение функции только для тех значений аргумента, которые заданы в таблице. Однако оно позволяет высказать предположение об аналитическом представлении функции, и, применяя различные методы приближенных вычислений, найти это представление.

Рассмотрим декартову систему координат на плоскости. Множество точек плоскости, координаты которых удовлетворяют условию , называется графиком функции y = f (x). Графическое представление функции удобно для непосредственного восприятия ее особенностей, описания свойств. Однако графический способ неудобен при выполнении расчетов.

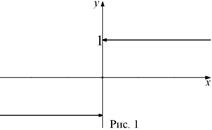Функции можно также задавать словесно. Например, функция Дирихле задается таким описанием: значение функции равно 1, если x рационально, и 0, если x иррационально.

Примеры функций:

x

1. Функция каждому положительному числу х ставит в соответствие число 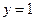, каждому отрицательному числу х ставит в соответствие число и (рис. 1). Эта функция называется знаком числа х и обозначается .

2. Функция каждому числу , где n Î ¢, ставит в соответствие число n (рис. 2). Эта функция называется целой частью числа х и обозначается .

3. Функция каждому числу , где n Î ¢, ставит в соответствие число (рис. 3). Эта функция называется дробной частью числа х и обозначается .

Сложная функция

Познакомимся с понятием суперпозиции функций, которое состоит в том, что в качестве аргумента одной функции используется другая функция. Полученная в результате суперпозиции функция называется сложной функцией. Записывается сложная функция следующим образом: . Например: , . Тогда сложная функция . Чтобы найти значение сложной функции, подставляют сначала заданное значение во внутреннюю функцию и находят ее значение , а затем уже вычисляют соответствующее значение функции .

При выполнении суперпозиции функций считают, что множество значений внутренней функции содержится в области определения внешней функции .

Сложную функцию можно составить из большего числа более простых функций.

Пример 1. Сложную функцию представьте в виде цепочки элементарных функций.

Решение. Будем последовательно выполнять операции, которые заданы в формуле: , , . Следовательно, заданная в условии задачи функция является суперпозицией трех основных элементарных функций.

Пример 2. Даны функции . Запишите сложную функцию .

Решение. Подставляя последовательно функции одну в другую, получим сложную функцию .

Обратная функция

Пусть функция , определенная на множестве Х, такова, что любым двум различным значениям аргумента х ставит в соответствие различные значения у, то есть, если 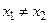, то . Эта функция устанавливает взаимнооднозначное соответствие между областью своего определения Х и областью изменения Y.

Действительно, каждой точке ставится в соответствие единственное . При этом каждой точке соответствует единственное , такое, что . Таким образом, на множестве Y определена функция , которая называется обратной к функции f. Область определения обратной функции – множество Y, область значений – множество Х. Графики функции и обратной к ней функции симметричны относительно прямой (рис. 4). Для обратных функций верно соотношение .

Для нахождения обратной функции необходимо из равенства выразить х через у, и в полученном выражении 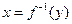букву х заменить буквой у, букву у – буквой х.

Пример 3. Имеют ли функции и обратные? Если да, то найдите их.

Решение. Выразим х из формулы . Получим . Обозначив аргумент через х, а функцию через у, получим , то есть функция является обратной к функции .

Функция не имеет обратной, так как она не является взаимнооднозначной. Действительно, .

Пример 4. Являются ли функции и взаимнообратными?

Решение. Нет, так как . Однако, если данные функции рассматривать только при , то есть считать , то эти функции становятся взаимнообратными.

Свойства функций

Определение 1. Функция называется монотонно возрастающей на множестве , если для любой пары точек из условия следует, что , то есть большему значению аргумента соответствует большее значение функции.

Определение 2. Функция называется монотонно убывающей на множестве , если для любой пары точек из условия следует, что , то есть большему значению аргумента соответствует меньшее значение функции.

Монотонно возрастающие и монотонно убывающие функции называют монотонными.

Монотонные функции обладают следующими свойствами:

1) сумма двух монотонно возрастающих (монотонно убывающих) функций является монотонно возрастающей (монотонно убывающей) функцией;

2) произведение двух положительных монотонно возрастающих (монотонно убывающих) функций является монотонно возрастающей (монотонно убывающей) функцией;

3) если функция монотонно возрастающая (монотонно убывающая), то функция 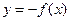монотонно убывающая (монотонно возрастающая);

4) если положительная функция является монотонно возрастающей (монотонно убывающей), то функция является монотонно убывающей (монотонно возрастающей);

5) если функция монотонная, то она имеет обратную функцию.

Определение 3. Функция называется ограниченной сверху на множестве , если существует такое число М, что значение функции в любой точке не превосходит этого числа, то есть для любого выполняется неравенство .

Определение 4. Функция называется ограниченной снизу на множестве , если существует такое число m, что значение функции в любой точке не меньше этого числа, то есть для любого выполняется неравенство .

Ограниченная сверху и снизу на множестве Х функция называется ограниченной на этом множестве. Другими словами, если функция ограничена на множестве Х, то существуют такие числа m и М, что для всех . Условие ограниченности можно также записать в виде для некоторого положительного числа М.

Определение 5. Точка называется точкой максимума функции , если существует окрестность этой точки такая, что для всех точек из этой окрестности выполняется неравенство .

Определение 6. Точка называется точкой минимума функции , если существует окрестность этой точки такая, что для всех точек из этой окрестности выполняется неравенство .

Точки максимума и минимума называют точками экстремума функции.

Заметим, что функция в области своего определения может иметь несколько точек максимума или минимума.

Определение 7. Будем говорить, что в точке функция принимает наибольшее на множестве Х значение, если для всех точек справедливо неравенство .

Определение 8. Будем говорить, что в точке функция принимает наименьшее на множестве Х значение, если для всех точек справедливо неравенство .

Если множество Х представляет собой отрезок [ a; b ], то наибольшее и наименьшее значения функция принимает либо в точке экстремума, либо на конце отрезка.

Говорят, что множество Х симметрично относительно начала координат, если для любой точки противоположная точка .

Определение 9. Функция называется четной, если ее область определения симметрична относительно начала координат, и для любого .

Определение 10. Функция называется нечетной, если ее область определения симметрична относительно начала координат, и для любого .

График четной функции имеет ось симметрии: так как точки и принадлежат графику функции, то он симметричен относительно оси ординат. График нечетной функции имеет центр симметрии: так как точки и принадлежат графику функции, то он симметричен относительно начала координат.

Четные и нечетные функции обладают следующими свойствами:

1) сумма двух четных (нечетных) функций есть функция четная (нечетная);

2) произведение двух четных (нечетных) функций есть функция четная; произведение четной и нечетной функций есть функция нечетная;

3) если нечетная функция определена в нуле, то ;

4) всякая функция, определенная на множестве Х, симметричном относительно начала координат может быть представлена в виде суммы двух функций, определенных на Х, причем одна из этих функций является четной, а другая – нечетной.

Определение 11. Функция называется периодической, если существует такое число , что для любого точка и справедливо равенство .

Наименьшее из чисел Т в определении 11 называют периодом. Периодическая функция имеет бесконечно много периодов, все они кратны числу Т.

Все введенные в этом параграфе определения используются при исследовании функций и построении графиков.