В данном пособии рассматриваются физические О, Ф, ФО − физические системы, состояние которых определяют происходящие в них процессы с учетом воздействия окружающей обстановки. Измерить физический объект или фон значит получить количественную информацию об этих процессах, протекающих в физических системах объекта и фона, описыва –
емых физическими величинами.
Физическая величина (ФВ) – свойство, общее в качественном отношении для многих физических объектов и индивидуальное в количественном отношении для каждого из них. Например, сила токамасса тела – общее свойство для любого физического объекта электрических цепей, имеет разное количественное значение для каждого из нихконкретных объектов.
Свойства физических объектов в наиболее общем виде сосредоточены в трех отношениях: эквивалентности (данное свойство у различных объектов одинаково или неодинаково); порядка (данное свойство у различных объектов больше или меньше); аддитивности (однородные свойства различных объектов могут суммироваться). Однородные свойства можно сравнивать, например, номиналы сопротивлений, температуру в помещении и на улице. Неоднородные свойства нельзя сравнивать, например, ток и напряжение в электрической цепи.
Величины делятся на два вида: реальные и идеальные (в основном математические). Реальные величины делятся на физические (ФВ) и нефи –
зические. Метрология исследует ФВ. Различают оцениваемые и измеряемые
ФВ.
Оцениваемая ФВ характеризуется числом, которое ей приписывается на основании экспертных, балльных, тестовых или др. показателей.
Измеряемая ФВ имеет определенное число единиц этой величины согласно уравнению измерения:
Q = q ·[ Q ], (1.11.1)
где Q, q – истинное, числовое значения ФВ, соответственно; [ Q ] – единица ФВ.
Упорядоченная совокупность значений ФВ, служащая основой для измерения ФВ, называется шкалой физической величины.
Различают измерительные шкалы:
• наименований (классификаций), например, атлас цветов: оцифровка оттенков и компьютерные технологии позволяют с минимальной погреш –
ностью колеровать краски; экспертные оценки запахов и др.;
• порядка (рангов), –- шкалы твердости Бринелля, Виккерса. Например, разработана технология для сертификации автомобильных стекол, в которой твердость определяется по шкале Бриннеля с использованием измерительного преобразования в виде отношения усилия, создава –
емого при вдавливании стального шара в стекло, к площади отпечатка на
испытуемом образце. Шкала Виккерса предполагает применение алмазной пирамидки вместо стального шара. Кроме измерительного преобразования,
используется условная шкала с опорными (реперными) точками – шкала Мооса для определения твердости минералов с условными числами твердости: 1 – тальк, 2 – гипс, 3 – кальций, 4 – флюорит, 5 – апатит, 6 – ортоклаз, 7 – кварц, 8 – топаз, 9 – корунд, 10 – алмаз. Если, например, после царапания материала корундом на нем остается царапина, а топазом нет, твердость испытуемого материала составит более 8, но менее 9 условных чисел;
• интервалов (разностей) –- например, температурные шкалы Цельсия, Фаренгейта, Реомюра;
• отношений, например, шкалы: массы; длины; силы электрического тока; электрического напряжения; термодинамической температуры, связанной с
шкалой Кельвина;
• абсолютные –- шкалы коэффициентов усиления, ослабления с безразмерной
единицей измерения.
В метрологии для установления различия в количественном содержании свойства, описываемого ФВ, введены понятия размерности и размера.
Размерность – качественная характеристика, отражающая различия между физическими величинами. Размерность физических величин обозначается прописными латинскими или греческими буквами.
Размер – количество единиц принятой размерности в данном свойстве объекта.
В В целях достижения единообразия в выражении результатов измерений физических величин с XVIII − XIX в.в. с целью достижения единообразия в выражении результатов измерения физических величин начавелась разработка международной системы единиц. Методика построения системы, предложенная К. Гауссом, заключалась в том, что основу системы формируют изсоставляют несколькоих физических величин, единицы которых выбирают независимо одна от другой и называют основными единицами системы. Остальные единицы системы называют производными, их единицы определяют через основные с помощью физических законов и соотношений – уравнений связи между величинами.
Широко известны следующие системы единиц.
СГС – установлены в качестве основных: единицы длины санти –
метр, массы грамм, времени секунда (принята в 1881 г.).
МКГСС – основные единицы: длины метр, силы килограмм-сила, времени секунда (конец XIX в.).
МКСА – основные: единицы длины метр, массы килограмм, времени секунда, силы тока ампер (1901 г.).
SI – первая система единиц физических величин, признанная на международном уровне, была утверждена XI Генеральной конференцией по мерам и весам в октябре 1960 года и в 1971 г. дополнена седьмой основной единицей – количество вещества моль. Система была названа System International of Unites – Международная система единиц SI. На ее основе разработан ГОСТ 8.417 – 81 «Единицы физических величин», введенный в действие с 1 января 1982 года. В настоящем издании для обозначения названной системы единиц используется аббревиатура SI, поскольку в Российской Федерации аббревиатура СИ широко применяется для сокращения другого термина «средство измерения».
История развития систем единиц физических величин отражает постоянный поиск методов и средств, обеспечивающих повышение точности измерений. В начале XX в. потребовалось дополнить основные единицы новой – сила тока ампер. На рубеже XX и XXI в.в. возникла необходимость освоения оптического диапазана электромагнитного спектра, что потребовало ввести в число основных единиц силу света кандела. Развитие технологии новых материалов стимулировало введение еще одной основной единицы – количество вещества моль.
В настоящее время система единиц SI включает семь основных (таблица 1.1), две дополнительные (таблица 1.2), большое количество производных единиц (таблицы 1.3… 1.5), а также внесис –
темные единицы, применяемые наравне с единицами SI (таблица 1.6), а также множители и приставки для образования десятичных кратных и дольных единиц (таблица 1.7).
К числу достоинств системы единиц SI относятся: универсальность, поскольку она охватывает в настоящее время все области науки и техники, а также практичность, так как в ней применены известные и широко распространенные единицы.
Основные единицы системы SIпредставлены в таблице 2.1.
Таблица 1.1. Таблица 2.1.
| № | Наименование | Обоз – начение русское, между – народное | Определение, формула | Размер ность | Единица измерения |
| Единица Ддлинаы | Русское м, m латинское m | Путь, пройден –ный светом в вакууме за интервал времени (299792458)--1с. | L | метр м, m | |
| Единица Ммассаы | кг, kg | Масса между –народного прототипа килограмма | M M | килограмм кг, kg | |
| Единица времени | с, s | периодов излучения перехода между двумя уровнями атома цезия-133 | T | секунда | |
| Единица термоди − намической температуры | К, К | (273,16) – 1 часть термодинамической температуры тройной точки воды | Ө | кельвин | |
| Единица количества вещества | моль, mol | Содержит столько же структурных элементов, сколько имеется атомов в углероде -12 массой 0,012 кг | N | моль | |
| Единица силы электрического тока | А, A | Сила неизменяющегося тока, который при прохождении по двум параллельным прямолинейным проводникам беско – нечной длины и нич –тожно малой площа - ди кругового попереч ного сечения, рас – положенным в вакууме на расстоянии 1 м один от другого, вызвал бы на каждом участке проводника длиной 1 м силу взаимодействия, рав – ную 2·10-7 Н | I | ампер | |
| Единица силы света | кд, cd | Сила света в заданном направлении источ –ника, испускающего монохроматическое излучение частотой 540 · 1012 Гц, энерге –тическая сила света которого в этом направлении состав –ляет 1/(683) Вт/ср. | J | кандела |
1. Метр (русское м, латинское m, размерность L) – единица длины, равная расстоянию, пройденному светом в вакууме за интервал времени 1/(299792458) секунды;
2. Килограмм (кг, kg, размерность М) – единица массы, равная массе международного прототипа килограмма;
3. Секунда (с, s, размерность Т) – единица времени, равная 9192631770 периодам излучения, соответствующего переходу между двумя сверхтонкими уровнями основного состояния атома цезия-133.
4. Кельвин (К, К, размерность Θ) – единица термодинамической температуры равная 1/(273,16) части термодинамической температуры тройной точки воды
5. Моль (Моль, mol, размерность N) – единица количества вещества, равная количеству вещества системы, содержащей столько же структурных элементов, сколько содержится атомов в углероде-12 массой 0,012 кг.
6. Ампер (А, А, размерность I) – единица силы электрического тока, равная силе неизменяющегося тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малой площади кругового поперечного сечения, расположенным в вакууме на расстоянии 1 м один от другого, вызвал бы на каждом участке проводника длиной 1 метр силу взаимодействия, равную 2·10 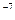 ньютона (Н, N).
ньютона (Н, N).
7. Кандела (кд, cd, размерность J) – единица силы света, равная силе света в заданном направлении источника, испускающего монохроматическое излучение частотой 540 · 1012 Гц, энергетическая сила света которого в этом направлении составляет 1/(683) Вт/с Дополнительные единицы системы SI, табл. 1.2:
Таблица 1.2.
| № | Наименование | Обоз – начение | Определение, формула | Размер ность | Единица измерения |
| Единица плоского угла | рад, rad | Равна внутреннему углу между двумя радиусами окружности, длина дуги между которыми равна радиусу. Величина полного угла равна 2 π радиан | Без – раз –мерная | радиан | |
| Единица телесного угла | ср, sr | Равна телесному углу с вершиной в центре сферы, вырезающему на поверхности сферы площадь, равную площади квадрата со стороной, равной радиусу | Без – раз –мерная | стерадиан |
• Радиан (рад, rad) − единица измерения плоского угла, равная внутреннему углу между двумя радиусами окружности, длина дуги между которыми равна радиусу. Величина полного угла равна 2π радиан.
• Стерадиан (ср, sr) − единица телесного угла, равная телесному углу с вершиной в центре сферы, вырезающему на поверхности сферы площадь, равную площади квадрата со стороной, равной радиусу.
Производные единицы в SI образуются из основных и дополнительных по уравнениям связи между физическими величинами. При этом система единиц SI остается когерентной. Когерентность обеспечивается путем введения в уравнения связи коэффициентов, которые приводят к единичному значению получаемой производной единицы.
Производные единицы физических величин в механике, электро- и магнитометрии, табл. 1.3. (Таблица из Куликова, с 25).
а) в механике (Куликов)
б) в электро- и магнетометрии (Куликов)
в) в фотометрии Таблица 1.3.
| № | Наимено – вание ве – личины | Обозначение | Определение, формула | Размерность | Единица измерения |
Производные единицы в механике
| Частота | f | f =1/Т 1/с | Т-1 | герц (Гц, Hz) | |
| Сила | F | F = ma кг· м / c 2 | LMT-2 | ньютон(Н,N) | |
| Давление,ме ханическое напряжение | p, σ | p = F/s Н/м2 σ = F/s Н/м2 | L-1MT-2 | паскаль (Па, Pa) | |
| Энергия, работа, ко – личество тепла | A | A = FL Н·м | L2MT-2 | джоуль (Дж, J) | |
| Мощность, поток энергии | P | P= A/T Н·м/c | L2MT-3 | ватт (Вт, W) |
Производные единицы в электро-, магнито-, радиометрии
| Напряжение потенциал, ЭДС | U | U= P/I Вт/A | L2MT-3I-1 | вольт (В, V) | |
| Количество электричес – тва, заряд | Q | Q= I·T A· c | I·T | кулон (Кл, С) | |
| Электричес- кое сопротив – ление | r | r = U/I B/A | L2MT-3I-2 | ом (Ом, Ω) | |
| Электричес - кая проводи мость | g | g = 1/ r | L-2M-1T3I2 | сименс (См, S) | |
| Электричес - кая емкость | С | Q/ U Кл/В | L-2M-1T4I2 | фарад (Фа,F) | |
| Напряжен – ность магнитного поля | H | H = nI/l, A/м, где: n – число витков на 1 м соленоида длиной l | I/L | ампер на метр | |
| Поток магнит – ной индукции, магнитный поток | Ф | Ф = Q · r Кл ·Ом | L2MT-2I-1 | вебер (Вб, Wb) | |
| Плотность магнитного потока, маг – нитная индукция | В | В = Ф / S Кл· Ом | MT-2I-1 | тесла (Тл, Т) | |
| Индуктив – ность, взаимная индуктив – ность | L | L = Ф/I Вб/А | генри (Гн) | ||
| Активность радионук – лида | с−1 | T-1 | беккерель (Бк, Bq) | ||
| Поглощен – ная доза ионизиру – ющего излучения | м2·с−2 | L2T-2 | грей (Гр, Gy) | ||
| Эквивалент ная доза излучения | м2·с−2 | L2T-2 | зиверт (Зв,Sv) |
Производные единицы фотометрическихОсновные фотометрические величин, табл. 1.4.
Таблица 1.4. Фотометрические величины характеризуют оптическое излучение по его действию на селективные приемники оптического излучения – т.н. редуци –
рованные фотометрические величины, либо безотносительно к его действию на приемники излучения, на основе единиц энергии – энергетические фотометрические величины, см. Советский энциклопедический словарь под ред. Прохорова А.М. – М.: Советская энциклопедия, 1987. – 1600 с., а также [108; Руководящие документы, рекомендации и правила, 3…9].
| № | Наименованиевеличины | Обоз – наче – ние | Определение, формула | Размер – ность | Единица измерения |
| Световой поток | Ф υ | Мощность оптического излучения по его действию на селективный приемник света, спектральная чувствительность которого определя – ется функцией относительной спектральной световой эффектив ности излучения. Ф υ = J · d Ω, d Ω – заполненный излучением малый телесный угол | кд∙ср | люмен, (лм) | |
| Облученность | Е υ | Е υ = J · d Ω/(d A·cosθ) d A – малая площадь участка, испускающего излучение (либо облученного); θ – угол между перпендикуляром к этому участку и направлением излучения | кд∙ср∙м -2 | люкс, (лк) | |
| Яркость | L υ | L υ = J /(d A·cosθ) | кд/м 2 | кандела на квадрат – ный метр | |
| Поток излучения | Фe | средняя мощность излучения за время, значительно большее периода колебаний; характеризуется количеством энергии, переносимой электромагнитными волнами в единицу времени через какую – либо поверхность | Вт | ватт, (Вт) | |
| Сила излучения | I e | I e – пространственно – угловая плотность потока излучения. I e = d Фe/ d Ω | Вт/ср | ватт на стерадиан | |
| Облученность | Е e | Е e = d Фe/(d Acosθ), | Вт/м 2 | ватт на квадрат – ный метр | |
| Энергетичес – кая яркость | L e | L e = d 2Фe/(d Ω d Acosθ) = dΙ e/(d Acosθ) = dЕ e/(d Ωcosθ). | Вт∙ср -1 м -2 | ватт на стерадиан и на квад ратный метр |
Соотношение между энергетическими (обозначается подстрочным индексом e) и световыми единицами (индекс υ) называется механическим эквивалентом света (М. э. с.), составляющим 0.00146 Вт/лм при длине волны излучения λ ≈ 555 нм. Величина, обратная М. э. с., называется световой эффективностью излучения.
Фотометрические величины характеризуют оптическое излучение по его действию на селективные приемники оптического излучения (например, человеческий глаз) – т.н. редуцированные (световые) фотометрические величины, либо безотносительно к его действию на приемники излучения, на основе единиц энергии – энергетические фотометрические величины.
Так, например, облученности в строках 2 и 6 табл. 1.4 – термины тождественные, но физический смысл разный: в 2 световые, в 6 энергетические фотометрические величины. Индексы e, υ опускаются, когда исключена возможность различного толкования.
Важное значение имеют
В действующей международной системе единиц (СИ) выбраны следующие световые величины: основная – сила света I υ, (единица которой называется кандела, обозначение и размерность кд), и три производных – световой поток Ф υ (люмен, лм, размерность кд∙ср), облученность Е υ (люкс, лк, кд∙ср∙м-2), яркость L υ (кандела на квадратный метр, кд/м2, кд∙м-2).
От светового потока Ф υ, действующего на глаз, отличают энергетический поток Фe, регистрируемый ОЭА.
Поток излучения Фe – средняя мощность излучения за время, значительно большее периода колебаний; характеризуется количеством энергии, переносимой электромагнитными волнами в единицу времени через какую – либо поверхность. Основная единица энергетического потока излучения – ватт (Вт).
Соотношение между энергетическими (обозначается подстрочным индексом e) и световыми единицами (индекс υ) называется механическим эквивалентом света (М.э.с.), составляющим 0.00146 Вт/лм при длине волны излучения λ ≈ 555 нм. Величина, обратная М.э.с., называется световой эффективностью излучения. Индексы e, υ опускаются, когда исключена воз –
можность различного толкования.
Энергетическая яркость Le – поверхностно – пространственная плотность потока излучения, переносимого узким пучком с малой площади dА, равна отношению потока излучения d2Фe к геометрическому фактору этого пучка d2G = dΩ∙dA∙cosθ:
Le = d2Фe/(dΩdAcosθ) = dΙe/(dAcosθ) = dЕe/(dΩcosθ). (3.14)
Здесь dΩ – заполненный излучением малый телесный угол, dA – малая площадь участка, испускающего излучение (либо облученного), θ – угол между перпендикуляром к этому участку и направлением излучения. Энергетическая яркость измеряется в Вт∙ср-1м-2. Яркость может также определяться через отношение силы излучения dΙe элемента поверхности к площади его поверхности, перпендикулярной рассматриваемому направлению, либо через отношение облученности dЕe в точке плоскости, перпендикулярной направлению на источник, к элементарному телесному углу, в котором заключен поток, создающий эту освещенность, как можно видеть из соотношения (3.14).
Сила излучения Ie – пространственно – угловая плотность потока излучения. Равна отношению потока излучения, распространяющегося от источника внутри телесного угла, к величине этого телесного угла; единица измерения Вт/ср.
Облученность Еe в точке поверхности – отношение энергетического потока, падающего на элемент поверхности, к площади этого элемента. Единица измерения энергетической облученности Вт/м2.
энергетическая облученность
Фотометроптическиее параметры и характеристикисвойства веществ, сред и тел.
Основные свойства приведены в Разделе 3.
Их можно разделить на две группы: 1) описывающие свойства веществ, сред в данной точке и 2) дающие интегральные свойства тел, таблица 2.1.
Таблица 2.1 __________________________________________________________________
№ Наименование обо – Формула Размер – Единица
значение ность измерения
1 2 3 4 5 6 __________________________________________________________________
1) Свойства веществ, сред в данной точке
1. Показатель погло – а а = – Ф–1 d Ф а / dℓ L–1 м–1
щения.
2. Показатель рассеяния r r = – Ф–1 d Ф r / dℓ L–1 м–1
r = 2π 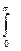 r (θ)sinθ d θ
r (θ)sinθ d θ
3. Индикатриса рассеяния Х (φ, θ) Х(φ, θ) = 4π r (φ, θ)/ r безразмерн.
1/2 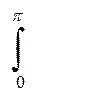 x (θ)sinθ d θ = 1
x (θ)sinθ d θ = 1
4. Показатель ослабления μ μ = – Ф–1 d Фμ/ dℓ L–1 м–1
μ = а + r
5. Вероятность выживания Λ Λ = r /μ = r /(а + r) безразмерн.
фотона
6. Показатель направленного r (θ,φ) r (θ) = Е n –І dІ (θ)/ d V L–1·ср-1 м–1·ср–1
рассеяния
7. Показатель рассеяния δ δ = 2π 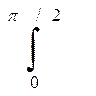 r (θ)sinθ d θ L–1 м–1
r (θ)sinθ d θ L–1 м–1
вперед
8. Показатель рассеяния β β = 2π r (θ)sinθ d θ L–1
назад
9. Коэффициент ассиметрии К К = δ/β безразмерн.
индикатрисы рассеяния
10. Показатель ассиметрии g g = (½)x(θ)cosθ sinθ d θ безразмерн.
рассеяния
2) Интегральные свойства тел
11. Оптическая длина пути s s = μ(x) d x безразмерн.
12. Коэффициент пропускания τ τ = Ф(ℓ)/Ф(0) = e–s безразмерн.
13. Коэффициент отражения ρ ρ = Фρ/Ф(0) безразмерн.
14. Коэффициент поглощения αα = Фα/Ф(0) безразмерн.
15. Коэффициент рассеяния σ σ = Фσ/Ф(0) безразмерн.
16. Коэффициент теплового ε ε = εи/εи0 безразмерн.
излучения
В таблице 2.1 применены следующие обозначения: Ф – поток параллельного монохроматического излучения, облучающий элементарный объем вещества d V, размер которого в направлении распространения излучения составляет dℓ; d Ф а, d Ф r, d Фμ – элементарные потоки излучения поглощенный, рассеянный и ослабленный, соответственно, при прохождении объема d V; Ф(0), Ф(ℓ), Фρ, Фσ, Фα – потоки монохроматического излучения на входе в среду, на выходе из слоя среды толщиной ℓ, отраженный от среды, рассеянный и поглощенный в среде соответственно; θ – угол между направ –
лениями падающего и рассеянного излучения (угол рассеяния); dІ (θ) – сила излучения, рассеиваемая объемом d V в направлении θ; E n – облученность (освещенность), создаваемая потоком Ф на поверхности объема d V, перпен –
дикулярной к направлению падающего излучения; εи, εи0 –энергетическая светимость теплового излучения данного объекта, черного тела соответст –
венно; x(θ) – индикатриса рассеяния (плотность вероятности рассеяния под углом θ).
Первые три характеристики табл. 2.1 называют основными, а характеристики 4 … 14, применяемые часто на практике, − производными, вытекающими из трех основных.
Следует отметить, что от общего пропускания среды, характеризуемого коэффициентом 12 табл. 2.1, отличают прозрачность среды, т.к. среда может быть непрозрачной, но пропускать рассеянное излучение (например, тонкий лист бумаги). Прозрачность связана только с коэффициентом направленного, но не диффузного, пропускания. В диапазоне видимого света сквозь тела из прозрачных сред при подходящих их геометрических формах предметы видны отчетливо.
Характеристики таблицы 2.1 зависят от длины волны излучения λ и должны применяться с указанием ее значения, либо спектрального интервала d λ. В этом случае они носят название спектральных показателей и коэффициентов.
Вывод формул для показателей а, r, μ однотипен. Приведем в качестве примера вывод формулы для показателя поглощения. Полагается, что параллельный поток излучения проходит в веществе элементарный слой толщиной dℓ. Тогда количество энергии, поглощенное этим слоем d Ф а, окажется пропорциональным энергии потока Ф и длине пути dℓ:
d Ф а = – а Ф dℓ.
Коэффициент пропорциональности а называется показателем поглощения.
Данная упрощенная модель является нестрогой, поскольку теоретическая фотометрия основывается на соотношении:
d Фe = L e d G,
выражающим в дифференциальной форме закон квадратов расстояний (об –
лученность Еe изменяется обратно пропорционально квадрату расстояния r
от точечного источника с силой света І, Е = І /r2, как установлено И. Кеплером в 1604 г.). Здесь d Фe – поток излучения элементарного пучка, d G = d Ω d Acosθ – геометрический фактор, L e – энергетическая яркость излучения.
Для яркости L (ℓ) пучка излучения, прошедшего в среде путь ℓ, согласно таблице 2.1 найдем
L (ℓ) = L (0)τ= L (0) e–s = L (0)e–μ*ℓ = L (0)·10–μ10 l,
где μ* = ℓ –1μ (x)dx – средний показатель ослабления в слое толщиной ℓ;
μ10 = Мμ*, М = lg e ≈ 0.4343…– прием записи, иногда используемый в светотехнике. Аналогично можно вводить десятичные показатели а 10 и r 10.
Индикатриса рассеяния.
Пусть падающий поток Ф создает на элементе объема d V = А dℓ облученность E n = Ф/А, где А площадь поперечного сечения, dℓ – длина элемента вдоль направления распространения излучения. Тогда сила излучения dΙ, рассеянного элементом d V в направлении угла θ, составит
dΙ = r (θ)En d V. (2.1)
Множитель r (θ) носит название показателя рассеяния в направлении θ.
Количество излучения, рассеянного элементом d V во всех направлениях равно d Ф r = ∫ dΙdω, но согласно табл.2.1 d Ф r = r Ф dℓ. Из (2.1) и выражений
4π
для d Ф r получаем
r = r (θ) dω = dφ r (θ)sinθ d θ = 2π r (θ)sinθ d θ. (2.2)
Равенство (2.2) преобразуем:
[ r (θ)/ r ] dω = Х (θ) dω /4π = 1,
где Х (θ) = 4π r (θ)/ r – индикатриса рассеяния, которую можно трактовать как плотность вероятности рассеяния под углом θ. Индикатриса рассеяния нормируется по условию
(1/2) Х (θ)sinθdθ = 1.
В зависимости от соотношения эффективного радиуса rэ элементарного объема dV и длины волны излучения λ можно условно выделить три класса явлений рассеяния: 1) rэ «λ, 2) rэ ≈ λ, 3) rэ» λ.
К первому классу относятся явления рассеяния: отдельными электронами
(томсоновское рассеяние света, при котором показатель или сечение расс е –
яния σ не зависит от частоты, σ = 8π/3r02= 6.65·10–25 см2, где r0 = e2/mc2 <<λ – классический радиус электрона, e и m –заряд и масса электрона); релеевское рассеяние отдельными атомами (σ ~ λ–4, когда частота падающего света ω мала по сравнению с частотой ω0 собственных колебаний атомных электронов, при резонансе ω = ω0 сечение резко возрастает, достигая значений λ2~10–10 см2); молекулами (наряду с несмещенными, рэлеевскими, в спектре рассеяния наблюдаются линии неупругого рассеяния, смещенные линии, интенсивности которых составляют 10–3…10–6 от интенсивности рэлеевских – т.н. комбинационное рассеяние света).
Ко второму классу относятся явления рассеяния малоразмерными частицами, которые могут быть описаны на основе теории дифракции света на диэлектрических частицах. Когда радиус частицы r меньше длины волны излучения λn в веществе, рассеяние на ней аналогично нерезонансному рассеянию атомом. Сечение рассеяния при этом зависит от r и разности диэлектрических проницаемостей ∆ рассеивающего вещества и окружающей среды: σ~λn– 4r6∆2 (Дж. У. Рэлей, 1871 г.). С ростом r до r ≈ λ и более индикатриса рассеяния становится изрезанной максимумами и минимумами вблизи резонансов Ми (2r = mλn, m =1, 2, 3, …; Г. Ми, 1908г.). В области резонансов сечения рассеяния возрастают до 6πr2; рассеяние вперед усиливается, назад ослабевает; зависимость поляризации излучения от угла рассеяния усложняется. Методики расчета индикатрисы силы рассеянного и отраженного излучения, а также коэффициентов экстинкции, рассеяния и обратного рассеяния на основе теории Ми позволяют исследовать рассеяние оптического излучения малоразмерных частиц с радиусом до ~ 1000 мкм. Рассеивающие свойства частиц полностью описываются 16 компонентами матрицы рассеяния Стокса [14,32]. Такие исследования дают возможность идентифицировать малоразмерные частицы по размеру, показателю преломления материала частиц (в случае определения всех параметров Стокса), что позволяет контролировать, например, засоренность техногенным мусором околоземного космического пространства. Для аналогичного контроля среднеразмерных (до 10 см) и крупных (объектов свыше 10 см) частиц целесообразно привлекать аппарат теоретической фотометрии в приближении диффузно – зеркального отражения [32].
Рассеяние излучения средами, состоящими из большого числа частиц (жидкими, твердотельными) отличается от рассеяния отдельными частицами в силу ряда факторов: взаимодействия частиц, многократного рассеяния (рассеянное одной частицей излучение вновь рассеивается другой), интерференции рассеянных частицами волн и падающей волны, влияния границ раздела и др.
Пример. Определим индикатрису рассеяния изотропно рассеивающей среды. Для нее индикатриса рассеяния постоянна по всем направлениям: Х (γ) = const. Из условия нормировки получаем:
(1/2)constsinθ d θ = 1. Внесистемные единицы, допускаемые к применению
наравне с единицами SI, табл. 1.5
Таблица 1.5.
| № | Наимено – вание величины | Наимено – вание единицы | Обоз – начение | Определение в единицах SI | ||||
| Время | минута час день | мин, min ч,h сут,d | 1 мин = 60 с 1 ч = 60 мин = 3600 с 1 сут = 24 ч = 86400 с | |||||
| Масса | тонна | Т,t | 1 т = 103 кг | |||||
| Плоский угол | градус минута секунда | º,º ´,´ ´´,´´ | 1º = (π/180) рад 1´ = (1/60)º=(π/10800) рад 1´´=(1/60)´=(π/648000) рад | |||||
| Объем | литр | л, L | 1 л = 1дм3 = 10-3м3 | |||||
| Уровень (логарифм отношения величины к ее исходно му значе – нию) | непер бел | Нп, Np B,Б | 1 Нп = 1
1 Б = (1/2)ln 10 Нп
Для энергетических
величин 1 Б = lg(P2/P1) при P2 = 10 P1. Для силовых величин 1 Б =2lg(F2/F1)
при F2 = 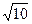 F1. F1.
| |||||
| Реактивная мощность | вар (вольт- ампер ре – активный) | Q | Q = I·U· sin φ переменного тока с разностью фаз φ между I и U | |||||
| Полная мощность | вольт-ампер | S | S = I·U переменного тока | |||||
Множители и приставки для образования десятичных кратных и дольных единиц SI, табл..1.6
Таблица 1.6
| № | Множитель | Наименование приставки русское, между – народное | Обозначение приставки русское, международное |
| 1024 | йота, yotta | И,Y | |
| 1021 | зета, zetta | З, Z | |
| 1018 | экса, exa | Э, Е | |
| 1015 | пета, peta | П, P | |
| 1012 | тера, tera | Т, T | |
| 109 | гига, giga | Г, G | |
| 106 | мега, mega | М, M | |
| 103 | кило, kilo | к, k | |
| 101 | дека, deca | да, da | |
| 10-1 | деци, deci | д, d | |
| 10-2 | санти, centi | с, с | |
| 10-3 | милли, milli | м, m | |
| 10-6 | микро, micro | мк, μ | |
| 10-9 | нано, nano | н, n | |
| 10-12 | пико, pico | п, p | |
| 10-15 | фемто, femto | ф, f | |
| 10-18 | атто, atto | а, a | |
| 10-21 | зепто, zepto | з, z | |
| 10-24 | йокто, yocto | и, y |
Основные рекомендации по применению приставок:
• В процессе вычислений для использования только когерентных единиц
все величины необходимо выражать в единицах СИ, а кратные и дольные
приставки подставлять в конечный результат, чтобы числовые значения
искомой величины находились в интервале 0,1…1000.
• Применение двух и более приставок подряд не допускается. Например,
вместо мегамегаГц должно быть применено наименование единицы
тераГц (ТГц).
• Приставку следует присоединять к наименованию первой единицы.
Например, правильно: киловатт-час, неправильно: ватт-килочас и т.п.
• Имеются исключения, например, тонна-километр (т-км), ампер на квадратный миллиметр (А/мм2).
• Склонение наименований производных единиц осуществляется изменением
последнего наименования и относящегося к нему прилагательного:
киловатт-часа, ньютон-секунды и др.
• Результат опыта, расчета должен содержать цифровое значение
величины с указанием единицы измерения, например 10.05 ± 0.01 В.
• В тексте отчета о лабораторно-практической работе использование обозначения единицы без указания численного значения величины недопустимо. Правильно: «Результаты расчета приведены в процентах», неправильно: «Результаты расчета приведены в %».
Наряду с десятичной метрической системой СИ на практике применяются другие единицы измерений. Например, в англоязычных странах используется система, основными единицами которой служат: фут (0,3048 м), фунт (0, 45359237 кг), секунда, ампер, градус Ренкина (ºRa = 5/9 К), кандела.
Создатели автомобилей указывают мощность двигателя в лошадиных силах (1 л.с. = 735,499 Вт), количество бензина в галлонах. Астрономы для измерения расстояний используют парсек и световой год; моряки – милю (1,852 км) и узел (0,514 м/с) как единицы длины и скорости; оптики – диоптрию в качестве единицы оптической силы; ювелиры – карат и унцию как единицы массы и т. п.






