| Степень точности ГОСТ 1643 - 81 | Твердость поверхно-стей зубьев | Коэффици-енты | Окружная скорость v, м/с | ||||
| ≤ 350 НВ | КНv | 1,03 1,01 | 1,09 1,03 | 11,16 1,06 | 1,25 1,09 | 1,32 1,13 | |
| KFv | 1,06 1,03 | 1,18 1,09 | 1,32 1,13 | 1,50 1,20 | 1,64 1,26 | ||
| > 350 НВ | КНv | 1,02 1,01 | 1,06 1,03 | 1,10 1,04 | 1,16 1,06 | 1,20 1,08 | |
| KFv | 1,02 1,01 | 1,06 1,03 | 1,10 1,04 | 1,16 1,06 | 1,20 1,08 | ||
| ≤ 350 НВ | КНv | 1,04 1,02 | 1,12 1,06 | 1,20 1,08 | 1,32 1,13 | 1,40 1,16 | |
| KFv | 1,08 1,03 | 1,24 1,09 | 1,40 1,16 | 1,64 1,25 | 1,80 1,32 | ||
| > 350 НВ | КНv | 1,02 1,01 | 1,06 1,03 | 1,12 1,05 | 1,19 1,08 | 1,25 1,10 | |
| KFv | 1,02 1,01 | 1,06 1,03 | 1,12 1,05 | 1,19 1,08 | 1,25 1,10 | ||
| ≤ 350 НВ | КНv | 1,05 1,02 | 1,15 1,06 | 1,24 1,10 | 1,38 1,15 | 1,48 1,19 | |
| KFv | 1,10 1,04 | 1,30 1,12 | 1,48 1,19 | 1,77 1,30 | 1,96 1,38 | ||
| > 350 НВ | КНv | 1,03 1,01 | 1,09 1,03 | 1,15 1,06 | 1,24 1,09 | 1,30 1,12 | |
| KFv | 1,03 1,01 | 1,09 1,03 | 1,15 1,06 | 1,24 1,09 | 1,30 1,12 | ||
| ≤ 350 НВ | КНv | 1,06 1,02 | 1,12 1,06 | 1,28 1,11 | 1,45 1,18 | 1,56 1,22 | |
| KFv | 1,11 1,04 | 1,33 1,12 | 1,56 1,22 | 1,90 1,36 | - 1,45 | ||
| > 350 НВ | КНv | 1,03 1,01 | 1,09 1,03 | 1,17 1,07 | 1,28 1,11 | 1,35 1,14 | |
| KFv | 1,03 1,01 | 1,09 1,03 | 1,17 1,07 | 1,28 1,11 | 1,35 1,14 |
Примечание: верхние числа – для прямозубых колес, нижние числа – для косозубых колес.
9.4. Коэффициент динамичности нагрузки при расчете контактных напряжений учитывает динамику нагружения, погрешности профилей зубьев, ошибки шагов зацепления шестерни и колеса. Значение КНv определяют при помощи таблицы 2.9.1 в зависимости от твердости рабочих поверхностей, степени точности передачи (см. 9.4.2) и окружной скорости (см. 9.4.1).
9.4.1. Линейная окружная скорость
,м/с (36)
9.4.2. Рекомендуемое значение степени точности изготовления Np можно выбрать по окружной скорости
при β > 0; (37)
при β = 0, (38)
где int – целая часть действительной переменной.
9.5. Коэффициент неравномерности нагружения зубьев для прямозубых передач КНα = 1, для косозубых передач вычисляют по формуле
. (39)
Полученное расчетное контактное напряжение должно находиться в интервале
, (40)
Если это условие не выполняется, необходимо выполнить перерасчет
передачи, корректируя ширину зубчатого венца колеса b 2 или межосевое расстояние a w. Если увеличивать b 2 или a w, то перегрузка уменьшится, уменьшив b 2 или a w, можно снизить недогрузку.
10. Проверка выполнения условия прочности по напряжениям изгиба
, (41)
где Т 2 - номинальный вращающий момент на колесе, Н·м;
u – передаточное число;
aw – межосевое расстояние, мм;
b2 – ширина зубчатого венца колеса, мм;
mn – нормальный модуль зацепления, мм (см. 6);
КFβ – коэффициент концентрации нагрузки (см. 6.2.1);
КFα - коэффициент неравномерности нагружения зубьев (см. 10.1);
YF – коэффициент формы зуба (см. 10.2);
Yβ – коэффициент, учитывающий угол наклона зубьев (см. 10.3).
10.1. Коэффициент неравномерности нагружения зубьев:
для косозубых передач 
; (42)
для прямозубых передач KFα = 1. (43)
10.2. Коэффициент формы зуба 
представляет собой чисто геометрический параметр, величина которого может быть определена с помощью следующих аппроксимирующих зависимостей:
- для колеса внешнего зацепления
; (44)
- для колеса внутреннего зацепления
, (45)
где z и z0 – числа зубьев колеса и долбяка соответственно;
x – коэффициент смещения инструмента при нарезании зубчатого колеса.
При практическом применении для колес внутреннего зацепления приближенно можно применять YF = 3,5…4,0; для колес внешнего зацепления при выборе коэффициента YF можно использовать специальные графики, представленные на рисунке 10.
10.3. Коэффициент, учитывающий угол наклона зубьев для косозубых и шевронных передач можно приближенно рассчитать по формуле
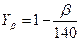, (46)
где β – угол наклона зубьев в градусах.
Для прямозубых передач Yβ = 1.
zv
Рис. 10. График для определения коэффициента формы зуба
x - коэффициент смещения инструмента при нарезании зубчатого колеса; zv – эквивалентное число зубьев (для шестерни 
, для колеса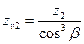 
)
Проверка условия прочности на изгиб должна быть выполнена для зубьев колеса и шестерни:
- для колеса 
; (47)
- для шестерни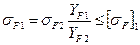 
; (48)
если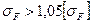 
, то необходимо увеличить значение модуля или ширины зубчатого венца с последующим перерасчетом геометрических параметров передачи.
11. Силы в зацеплении цилиндрической зубчатой передачи
Рис. 11. Силы, действующие в зацеплении цилиндрической косозубой передачи
(α – угол профиля; β – угол наклона зубьев).
Нагрузка в контакте зубчатых колес представляет собой нормальную силу Fn, составляющие которой называются окружной Ft, радиальной Fr и осевой Fa проекциями (см. рис. 11); 
- проекция полной нормальной силы на горизонтальную плоскость.
, (49)
где T2 – вращающий момент на колесе, Н·м;
d2 – делительный диаметр колеса, мм.
; (50)
(51)
Глава 3
