Три уравнения Лауэ, определяющие направление интерференционных максимумов, можно свести к одному, общему интерференционному уравнению, которое записывается в векторной форме.
Рассмотрим так же, как и раньше, дифракцию рентгеновских лучей на атомном ряде. Разность хода двух соседних лучей после дифракции от атомного ряда равна a×cosa - a×cosa0 (рис.2.7). Для того, чтобы учесть направление падающего и рассеянного луча в пространстве, введем единичные вектора S0 и S. По абсолютной величине они равны 1, а по направлению S0 - совпадает с направлением первичного пучка, а S - направлением дифрагированных лучей. Разность хода двух соседних лучей определим как a×cos a×1 - a×cosa0×1 = (a [ S - S0 ]). Дифракционный максимум мы получим, когда на длине этого отрезка укладывается целое число длин волн, т.е.
(a [ S - S0 ]) = ml. (2.24 а)
Аналогичным образом можно преобразовать и другие уравнения Лауэ, записав их в векторной форме:
(b [ S - S0 ]) = nl, (c [ S - S0) = pl. (2.24 б)
Разделив левую и правую части этих уравнений на l, получим:

 (2.25)
(2.25)


Если в обратной решетке взять точку - узел с индексами m, n и p, то вектор H, проведенный в эту точку, запишется как
H = m a *+ n b * + p c *. (2.26)
Тогда, умножив скалярно левую и правую части этого выражения на a, а затем последовательно на b и с, будем иметь
 (2.27)
(2.27)
Сопоставляя между собой систему уравнений (2.26) и (2.27), получим новое фундаментальное соотношение:
(S - S0)/l = H (2.28)
которое полностью определяет направление дифракционных максимумов и содержит в себе все 3 уравнения Лауэ. Действительно, умножив левую и правую части уравнения (2.28) на вектор a, получим первое уравнение Лауэ и при умножении на вектора b и c соответственно второе и третье уравнения Лауэ.
Графическое выражение интерференционного уравнения. Сфера отражения или сфера Эвальда. Общее интерференционное уравнение можно выразить графически, используя построение обратной решетки кристалла (рис. 2.10).

Рис.2.10. Сфера Эвальда.
Построим обратную решетку кристалла. Для этого, проведем из какой-либо точки O, связанной с кристаллом, оси обратной решетки (см. построение обратной решетки). Зная направление осей и величины единичных векторов, строим координатную сетку. Узлы ее будут одновременно узлами обратной решетки кристалла. Для простоты нарис.2.10 представлена двухмерная сетка. Допустим, что направление падающего пучка S0. Выбираем луч, который проходит через начало координат. Отложим от начала координат (точки O) вектор –S0 /l, конец которого будет какой-то точкой A. По абсолютной величине этот вектор равен 1/l, т.к. | S0 |=1. Опишем из точки A сферу радиусом 1/l. По положению она жестко связана с направлением первичного пучка и всегда проходит через начало координат. Построенная сфера носит название сферы отражений или сферы Эвальда.
Замечательной особенностью этой сферы является то, что для любого узла обратной решетки, попавшего на ее поверхность, удовлетворяется общее интерференционное уравнение. Возьмем, например, узел M на сфере и рассмотрим векторный треугольник OAM. Согласно известным правилам сложения векторов сумма OA + AM = OM. Так как вектор OM является не чем иным, как вектором H, а OA = –S0 /l можно записать
AM – S0 /l = H (2.29)
Из сравнения этого выражения с уравнением (2.28) следует, что вектор AM, равный 1/l, по направлению должен совпасть с S. В результате получим соотношение, являющееся общим интерференционным уравнением трехмерной решетки:
S /l –S0 /l = H (2.30)
Любой узел на сфере удовлетворяет общему интерференционному уравнению. В этом первое замечательное свойство сферы отражения. Кроме того, точки пересечения сферы отражения с узлами обратной решетки определяют направление дифракционного луча. Последнее, очевидно, совпадает с направлением вектора S /l. Из сказанного следует, что при заданных параметрах элементарной ячейки кристалла a, b, c и известной длине волны падающего пучка рентгеновских лучей l можно с помощью построения обратной решетки и сферы Эвальда установить направление всех интерференционных лучей в пространстве и, следовательно, установить вид рентгенограммы при том или ином положении рентгенопленки. Практически, однако, решают обратную задачу, рассчитывая по рентгенограмме, т.е. по положению интерференционных пятен, параметры ячейки кристалла a, b, c. Пользуясь сферой Эвальда, легко показать, как меняется дифракционная картина при повороте кристалла или изменении длины волны излучения. Действительно, диаметр сферы отражения равен 2/l. Поэтому при увеличении l размер сферы уменьшается. Если диаметр сферы станет меньше любого вектора H, то ни один узел обратной решетки не попадет на поверхность сферы, и дифракция станет невозможной. Таким образом, дифракция возможна (при l£ 2d), если
| H |< 2/l. (2.31)
Для изучения с l=2Å, условие дифракции выражается | H |=1/d <1Å. Следовательно, при d >1Å для кристаллов с межплоскостным расстоянием меньше 1 Å, дифракции не будет.
Дифракция как отражение
Пусть некоторый узел обратной решетки [[ HKL ]] попадает на сферу Эвальда. Соответствующая ему плоскость в кристалле с индексами (hkl) располагается нормально H (рис.2.11).
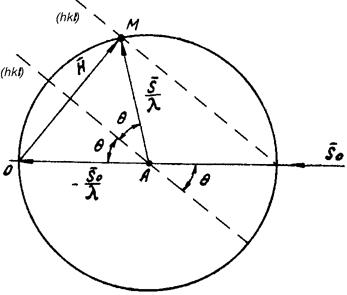
Рис. 2.11. Дифракция как отражение.
Проведем в обратной решетке через центр сферы плоскость, параллельную (hkl). Поскольку вектор H всегда перпендикулярен плоскости (hkl), то угол при вершине OAM, будет разделен надвое. Из этого следует, что углы между падающим лучем S0 и плоскостью (hkl), а также между отраженным лучем и (hkl) всегда равны между собой. На основании этого (hkl) можно рассматривать как плоскость, отражающую рентгеновские лучи, и процесс дифракции можно описывать как отражение рентгеновских лучей от семейства соответствующих плоскостей кристалла.
Действительно, в кристалле всегда можно найти плоскость, которая ориентирована к лучу дифракции как плоскость отражения. Это относится и ко всей системе плоскостей, параллельных данной. Поэтому каждый дифракционный луч может рассматриваться как “отраженный” от системы параллельных атомных сеток - плоскостей. Сфера Эвальда в этом случае позволяет выделить в кристалле отражающие плоскости, которые сопоставляются узлам, лежащим на поверхности сферы.
Уравнение Вульфа - Брегга
Для определения углов, при которых возможны отражения рентгеновских лучей, рассмотрим систему кристаллографических плоскостей с расстоянием между ними равным d, т.е. представим кристалл как систему атомных плоскостей (рис.2.12).

Рис. 2.12. К выводу уравнения Вульфа - Брегга.
Пусть падающий луч идет по направлению S0 и составляет угол q с плоскостью (hkl), а отраженный дифракционный луч идет по направлению S также под углом q к плоскости (hkl). Рассмотрим интерференцию отраженных волн от семейства параллельных плоскостей 1, 2, 3... с индексами (hkl). Рентгеновские лучи, проникая вглубь кристалла, будут отражаться не только от внешней 1-ой но и от внутренних 2, 3 и т.д. плоскостей. Отраженные от различных плоскостей лучи будут интерферировать между собой и усиливать друг друга, если разность хода лучей равна целому числу волн nl. Эту разность хода легко вычислить из рисунка 2.12. Она равна AB + BC = 2AB = 2d sinq. Посколькув направлении мы должны наблюдать луч дифракции, соответствующий максимуму интерференции, то
2d sinq = nl, (2.32)
где d - межплоскостное расстояние, n=1, 2, 3....
Это и есть формула Вульфа-Брегга. Угол q, входящий в нее, обычно называют углом скольжения или углом отражения; целое число n - порядком отражения.
Формула Вульфа-Брегга указывает на селективность (избирательность) появления отраженных рентгеновских лучей. В этом заключается отличие между отражением рентгеновских лучей от атомных плоскостей кристалла и отражением света от зеркала. Если для оптических лучей непрерывно менять угол между зеркалом и падающим лучем, то отраженный луч будет очень мало менять свою интенсивность. Для рентгеновских же лучей кривая интенсивности является кривой с резко выраженными максимумами. При этом условие дифракции выполняется только в том случае, когда
nl/2d = sinq £ 1 и nl£2d. (2.33)
Индексы интерференций. В формуле Вульфа-Брегга число n, называемое порядком отражения, показывает, какое число длин волн составляет разность хода падающих и отраженных лучей.
Преобразуем уравнение Вульфа-Брегга (2.32) и, разделив обе части его на n, получим
2(dhkl / n) sinq = l. (2.34)
В этой формуле множитель dhkl / n можно рассматривать, как межплоскостное расстояние новой системы (HKL) плоскостей. Эти плоскости реально могут и не существовать, но они должны удовлетворять условию:
dhkl / n=dHKL, (2.35)
где H, K, L - индексы фиктивной плоскости.
Индексы плоскости, как известно, обратно пропорциональны отрезкам, отсекаемым на осях координат и, следовательно, обратно пропорциональны межплоскостному расстоянию. Используя коэффициент пропорциональности p, запишем h=1/pa=1/pdhkl
H= 1/pdHKL=n/dhkl или H= nh.
Аналогично К= nk,
L=nl. (2.36)
Индексы H, K, L новой системы плоскостей называются индексами интерференции. Для системы (HKL) уравнение Вульфа-Брегга запишем как:
2dHKL×sinq=l. (2.37)
В последнем виде формула очень часто используется при индицировании рентгенограмм. Индексы интерференции используются при обозначении рефлексов на.рентгенограммах.
Пользуясь соотношением (2.37), всегда следует помнить, что межплоскостное расстояние в этой формуле может отвечать некоторой фиктивной плоскости (HKL), индексы которой (индексы интерференции) всегда имеют общий множитель n. Реально же отражение происходит от плоскостей с индексами в n раз меньше и при разности хода в n раз больше.
Например, пусть разность хода между плоскостями (001) с межплоскостным расстоянием d001 равна 4l. Тогда 2d001×sinq=4l или (2d001/4)sinq=l. Заменяя индексы реальных плоскостей (001) индексами интерференции, получим d/4=d¢ и 2d004×sinq=l, где d¢=d004. Таким образом, отражение от плоскости (001) с разностью хода, равной 4l, можно рассматривать условно как отражение от плоскости с индексами (004) и разностью хода l. Индексы содержат общий множитель, равный 4.






