ВВЕДЕНИЕ
Дисциплина «Электротехника и электроника» является одной из основных общетехнических дисциплин, необходимых для успешного освоения своей будущей профессии студентами, подготавливаемыми по неэлектротехнических направлениям.
При эксплуатации современного высокотехнологичного оборудования обслуживающему персоналу необходимо обеспечить высокую производительность машин и механизмов, надежное и безаварийное управление технологическими процессами. Для этого необходимы глубокие знания законов электромагнитных явлений, основных методов анализа электрических цепей и цепей электроники и умение применять их в новых технологиях, технологических процессах и электрооборудовании.
Глубокое изучение электротехнических дисциплин достигается выполнением практических заданий и решением задач по составлению схем замещения электроустановок, расчету электрических цепей в эксплуатационных и аварийных режимах работы, анализу режимов работы электроустановок, электрических машин и устройств электроники, используемых для управления технологическими процессами.
Поэтому наряду с изучением теоретических разделов дисциплины «Электротехника и электроника» студенты должны получить навыки расчетов токов, напряжений и мощностей в линейных и нелинейных цепях постоянного и переменного токов, при гармонических несинусоидальных воздействиях, работающих в установившихся и переходных режимах. Также необходимы навыки расчетов основных характеристик наиболее распространенных электромагнитных и электромеханических устройств, таких как трансформаторы, электродвигатели постоянного и переменного тока, работающих в нормальных и аварийных режимах.
При решении задач выполняются требования по разработке принципиальных схем электроустановок и их схем замещения, построению потенциальных и векторных диаграмм.
В пособии даны методические пояснения и приводятся примеры решения типовых задач по основным разделам дисциплины «Электротехника и электроника».
Материал учебного пособия может быть использован студентами очной формы обучения при выполнении расчетно-графических работ, а также при их подготовке к практическим занятиям, зачету или экзамену по дисциплине «Электротехника и электроника».
ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ
ПОСТОЯННОГО ТОКА
Элементы электрической цепи
Элементы электрической цепи делятся на активные и пассивные.
Элементы электрической цепи, не являющиеся источниками электрической энергии, называют пассивными.
Идеальным элементом, полностью рассеивающим электрическую мощность, является резистор. В соответствии с законом Джоуля-Ленца резистор преобразует электрическую энергию в тепловую. Зависимость напряжения от тока в таком элементе определяется законом Ома: UR(I)=R I.
К активным элементам относятся источники электрической энергии. Деление источников электрической энергии на источники ЭДС и тока – условное.
Источник ЭДС характеризуется неизменным значением ЭДС E и внутренним сопротивлением RВН. Внутреннее сопротивление RВН такого источника электрической энергии существенно меньше сопротивления нагрузки RН (RВН«RН), и в режиме идеализированного источника ЭДС им можно пренебречь (RВН=0).
Источник тока характеризуется неизменной величиной тока J и внутренней проводимостью GВН. Внутреннее сопротивление RВН такого источника электрической энергии много больше сопротивления нагрузки RН. При GВН=0 источник тока называют идеализированным, у которого RВН→∞.
Зависимость напряжения между положительным и отрицательным выводами источника от его тока называют внешней характеристикой источника электрической энергии.
Внешняя характеристика реального источника электрической энергии математически описывается уравнением:
,
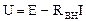где RВН – внутреннее сопротивление источника.
Этому уравнению соответствует схема замещения источника электрической энергии, состоящая из последовательно соединенных идеальных элементов: источника ЭДС и резистивного элемента с сопротивлением RВН. На рис. 1.1 принципиальная схема источника ЭДС обведена штриховой линией.
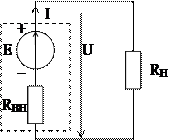
Рис. 1.1
При делении всех членов уравнения, описывающего внешнюю характеристику реального источника электрической энергии, на RВН, получают уравнение, которому соответствует принципиальная схема источника тока, представленная на рис. 1.2 участком, ограниченным штриховой линией:
,
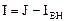где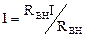 
; 
; 
.
. 
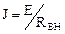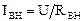Рис. 1.2
На рис. 1.3 представлена обобщенная вольт-амперная характеристика источника электрической энергии, на которой:
участку AB соответствует его работа в режиме активного приемника (потребления электрической энергии), когда направление тока совпадает с направлением напряжения и противоположно направлению ЭДС;
участку BC - его работа в генераторном режиме (отдачи электрической энергии), когда направление тока совпадает с направлением ЭДС и противоположно направлению напряжения;
участку CD - работа в режиме приемника, при котором направления тока, напряжения и ЭДС совпадают.
Рис. 1.3
1.1. Изобразите схему замещения цепи электроустановки (рис. 1.4).
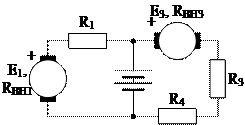
Рис. 1.4
1.2. К источнику электроэнергии подключен приемник с сопротивлением R = 12 Ом. Внешняя характеристика источника приведена на рис. 1.5. Изобразите схему замещения цепи. Определите внутреннее сопротивление источника RВН и напряжение на зажимах источника при включенном приемнике. 
Рис. 1.5
Мощности и КПД
Мощность, генерируемая источником ЭДС: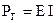 
.
Мощность, отдаваемая реальным источником ЭДС (полезная мощность):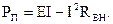 
Потери мощности 
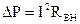расходуются на нагрев источника.
Коэффициент полезного действия источника электрической энергии в относительных единицах: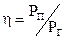 
.
Если источник энергии работает в режиме активного приёмника, то потребляемая им мощность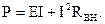 
Мощность, генерируемая источником тока: 
, где UJ – напряжение между положительным и отрицательным выводами источника тока.
Мощность, потребляемая пассивным приемником: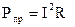 
.
1.3. Найти внутреннее сопротивление источника и его ЭДС, если при сопротивлении нагрузки 1 Ом ток равен 3 А, а при сопротивлении нагрузки 2,5 Ом ток равен 0.5 А. Определить мощность и КПД источника для этих режимов.
1.4. Определите напряжение на зажимах источника энергии и его внутреннее сопротивление (рис. 1.6). Дана ВАХ источника, полезная мощность Р=4 кВт; сопротивление нагрузки R=10 Ом.
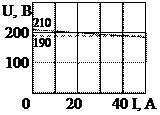
Рис. 1.6
1.5. Какой ЭДС должна обладать батарея, чтобы напряжение на зажимах приемника Uab было равным 24 В (рис. 1.7)?
Мощность, отдаваемая источником, 48 Вт; мощность внутренних потерь 1,2 Вт.
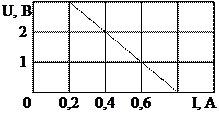
Рис. 1.7 Рис. 1.8
1.6. По заданной ВАХ (рис. 1.8) построить схему и определить ее параметр: а) для последовательной схемы замещения; б) для параллельной схемы замещения. Найти ток в приемнике сопротивлением R = 5 Ом, подключенном к данной схеме.
1.7. К источнику с известной внешней характеристикой (рис. 1.9) подключен резистор сопротивлением R = 2 кОм. Найти ток в цепи и мощность источника, а также параметры его схем замещения.
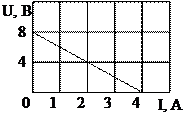
Рис. 1.9
Режимы работы электрических цепей
Номинальным называется режим, в котором электрическая цепь работает при номинальных значениях напряжения, тока и мощности (значения, на которые рассчитана цепь заводам – изготовителем).
Согласованным называется режим, в котором мощность, генерируемая источником или потребляемая приемником, имеет наибольшее значение. Условием такого режима является равенство сопротивления нагрузки и внутреннего сопротивления источника.
В режиме холостого хода ток через приемник электрической энергии не протекает, но на зажимах источников энергии присутствует напряжение, равное ЭДС источника (Uхх=E). В этом режиме источник не отдает энергию во внешнюю цепь, а преемник ее не потребляет.
Режим короткого замыкания наступает при случайном замыкании разноименных полюсов источника посторонними токопроводящими предметами (шунтами) или участка электрической цепи, находящегося под напряжением.
1.8. Напряжение на выходе усилителя постоянного тока (УПТ) (рис. 1.10) в режиме холостого хода U ХХ = 10 В, сопротивление усилителя относительно точек ab Rab = 0,2 кОм. Как изменится напряжение на выходе УПТ, если к усилителю подключить приемник с сопротивлением Rп = Rab. Пояснить, как зависит это напряжение: а) от сопротивления усилителя Rвых; б) сопротивления приемника Rп.
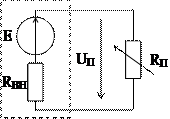
Рис. 1.10 Рис. 1.11
1.9. Построить внешнюю характеристику генератора постоянного тока (ГПТ) (рис. 1.11) и определить его КПД, если номинальные данные генератора: Uном = 230 В, I ном = 1 А, R = 15 Ом. Определить ток короткого замыкания ГПТ. Найти ток в цепи, мощность, генерируемую источником и мощность приемника, а также КПД источника.
Соединения элементов
При последовательном соединении элементов электрической цепи через них протекает один и тот же ток. В непосредственном электрическом контакте находятся только два элемента. На рис. 1.12, а представлена схема последовательного соединения пассивных элементов.
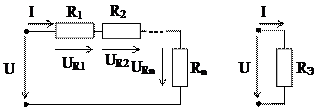
а) б)
Рис. 1.12
Эквивалентное сопротивление такой цепи (рис. 1.12, б) равно арифметической сумме значений последовательно включенных сопротивлений:
Если в непосредственном контакте находятся три и более элемента цепи, то это место называется узлом и обозначается точкой (·).
Если цепь имеет более одного узла, то элемент или группа последовательно соединенных элементов, включенных между двумя узлами, называется ветвью цепи. Вдоль ветви ток в любой момент времени имеет одно и то же значение.
При параллельном соединении ветви подсоединены к одной и той же паре узлов и находятся под одним и тем же напряжением. На рис. 1.13, а показана схема параллельного соединения пассивных элементов.
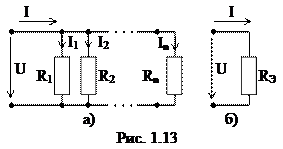
Эквивалентное сопротивление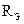 
(рис. 1.13, б) цепи определяется из соотношения:
Величину, обратную сопротивлению, называют проводимостью. Суммарная проводимость параллельно соединенных ветвей равна сумме проводимостей ветвей:
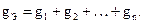
Для двух параллельно соединенных сопротивлений эквивалентное сопротивление равно: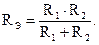 
Смешанное соединение образуют последовательно соединенные группы и параллельно включенные ветви, состоящих из последовательно соединенных элементов (рис.1.14).
В схеме рис. 1.6, состоящей из пассивных элементов, сначала определяют сопротивление каждой ветви:
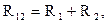
затем находят проводимость схемы между точками b и c как сумму проводимостей параллельных ветвей:
, 
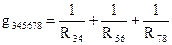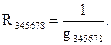
Рис. 1.14
Далее, складывая сопротивления последовательно соединенных участков ab и bc, определяют эквивалентное сопротивление цепи: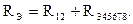 
Ветви сложноразветвленной цепи входят в состав «звезд» и «многоугольников». На рис. 1.15 показаны способы соединения трех сопротивлений, называемые соединением «треугольник» (∆) (рис. 1.7, а) и соединением - «звезда» (Y) (рис. 1.15, б).
В треугольнике три сопротивления образуют замкнутый контур, но каждая пара элементов имеет по одной общей точке. В звезде все сопротивления подключены к одному общему узлу, называемому нейтральной точкой.
а) б)
Рис. 1.15
При расчете электрических цепей довольно часто оказывается полезным преобразовать треугольник в эквивалентную заезду или наоборот, звезду в треугольник.
∆ ← Y Y ← ∆
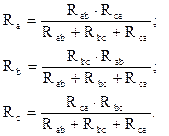
Согласно условию эквивалентности токи и напряжения в частях схемы, не затронутых преобразованием, остаются неизменными.
1.10. Определить эквивалентное сопротивление цепи относительно зажимов 1-1' цепи (рис. 1.16) при холостом ходе (зажимы 2-2' разомкнуты) и при коротком замыкании (зажимы 2-2' замкнуты). Значения сопротивлений указаны на схеме.
Решение. В режиме холостого хода, когда зажимы 2-2' разомкнуты, схему можно представить в виде, как показано на рис. 1.17, а. А в режиме короткого замыкания, когда зажимы 2-2' соединены проводником схему можно представить, как показано на рис. 1.17, б.
Рис. 1.16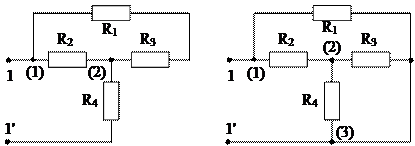 
а) б)
Рис. 1.17
В схеме а рис. 1.17 два узла, три ветви. Сопротивления R1 и R3 соединены последовательно.
Их эквивалентное сопротивление определяется как арифметическая сумма:
.
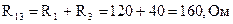Сопротивление R13 и сопротивление R2 присоединены к одной паре узлов и их эквивалентное сопротивление может быть определено:
.
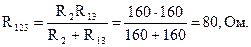Входное сопротивление цепи определяем как сумму сопротивлений R4 и полученного сопротивления R123, так как эти элементы соединены последовательно:
.
В схеме б рис. 1.17 три узла, 5 ветвей. Третья и четвертая ветви соединены параллельно, так как присоединены к одной паре узлов, и их эквивалентное сопротивление будет определяться:
.
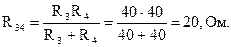Резистор с сопротивлением R2 и полученное сопротивление R34 включены последовательно:
Первая ветвь соединена параллельно с полученным эквивалентным резистором R234:
.
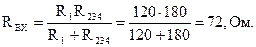1.11. Определить эквивалентное сопротивление цепей (рис. 1.18).
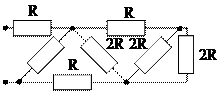
Рис.1.18
1.12. Определить эквивалентное сопротивление цепи (рис.1.19.), если: R1 = R5 = 4 Ом, R2 = 3,6 Ом, R3 = 6 Ом, R4 = 3 Ом.
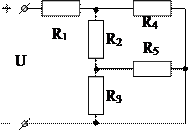
Рис. 1.19
Законы Ома определяют связь между основными электрическими величинами:
а) на участке линейной цепи с пассивными элементами:
,
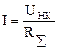где UНК - напряжение между началом и концом участка, совпадающее по направлению с током;
R∑-суммарное сопротивление участка;
б) на участке линейной цепи с активными и пассивными элементами:
где UНК - напряжение между началом и концом участка, совпадающее по направлению с током;
∑E- алгебраическая сумма ЭДС, действующих на выбранном участке;
R∑-суммарное сопротивление участка.
Примечание: если ЭДС совпадает по направлению с положительным направлением тока, то она записывается с положительным знаком, а если не совпадает - с отрицательным.
в) в замкнутой линейной цепи с активными и пассивными элементами:
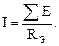
1.13. Определите напряжение Uab на зажимах участка цепи (рис. 1.20) для трех случаев: если а) I3= 0; б) I3= 3 А; в) I3=7 А. Е1=90 В; R1=6 Ом; I1=12 А; I2=7 А.
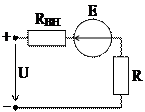
Рис. 1.20 Рис. 1.21
1.14. В каком режиме работает источник энергии с ЭДС Е (рис. 1.21)? Определите напряжение на его зажимах ab, если U=110 В; Е=80 В; R=37,3 Ом; Rвн=0,2 Ом.
1.15. Как изменяется яркости ламп после замыкания ключа (рис. 1.22)?
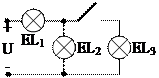
Рис. 1.22
1.16. Определить напряжение Uab на выходе потенциометра (рис.1.23) при трех положениях его движка:
а) в крайнем верхнем; б) в крайнем нижнем; в) в средней точке потенциометра, если U = 30 В, R = 20 Ом.
Рис. 1.23 Рис.1.24
1.17. Рассчитать сопротивления R1 и R2 высокоомного делителя напряжения (Рис. 1.24), если Uвх = 10 В, Uвых = 30 мВ, ток источника не должен превышать 100 мкА.
1.18. На какие значения сопротивления и тока следует выбирать реостат Rp цепи рис. 1.25, с помощью которого можно регулировать напряжение на потребителе Rп в пределах 40 ÷ 160 В, если U = 220 В, Rп = 20 Ом?
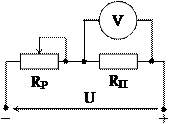
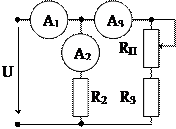
Рис. 1.25 Рис. 1.26
1.19. Определите, как изменятся показания амперметров при перемещение ползунка потенциометра RП вниз (рис. 1.26).
1.20. Милливольтметр на 100 мВ имеет внутреннее сопротивление 5 Ом. «Изготовить» из него: а) амперметр на 50А; б) вольтметр на 600 В.
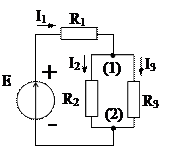
1.21. Рассчитать токи в ветвях электрической цепи, схема которой показана на рис. 1.27, а, если известны ее параметры: R1= 0,6 Ом; R2= 4 Ом; R3= 6 Ом; E=12 В.
Решение. Цепь содержит два узла, три ветви и один источник ЭДС (рис. 1.27, а). Токи в такой цепи направлены от точки с самым высоким потенциалом - (+) к точке с самым низким потенциалом - (-), и мы можем сразу показать положительные направления токов ветвей. Так как известна ЭДС источника, необходимо первоначально определить ток в ветви с источником.
Метод эквивалентных преобразований предусматривает постепенную замену пассивных участков цепи, представляющих собой последовательное или параллельное соединение приемников, эквивалентными сопротивлениями.
Вначале определяем эквивалентное сопротивление двух параллельных ветвей, подключенных к паре общих узлов (1) и (2) (рис. 1.27, а):
.
а) б)
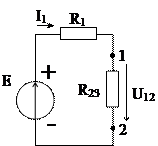
Рис. 1.27
Участок 1-2 преобразованной схемы (рис. 1.27, б) соединен последовательно с резистором R1 и вдоль него идет ток I1.
Эквивалентное сопротивление цепи относительно зажимов источника энергии:
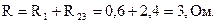
Далее по закону Ома для замкнутой цепи вычисляем ток в ветви с источником:
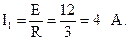
Воспользовавшись законом Ома для участка 1-2 в схеме а рис. 1.27 можно вычислить токи параллельных ветвей, но для этого нам необходимо знать напряжение между узлами (1) и (2). Для определения напряжения U12 воспользуемся схемой б рис. 1.27, в которой по участку 1-2 протекает ток I1, величина которого уже вычислена. По закону Ома:
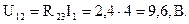
Тогда токи в параллельных ветвях (рис. 1.27, а):
Эти токи можно определить иначе, используя пропорцию:
1.22. Определите показание ваттметра в цепи (рис. 1.28) при включенном и отключенном выключателе SA. Дано: U=120 В; R1=5 Ом; R2=10 Ом; R3=60 Ом; R4=30 Ом; R5=15 Ом.
Рис. 1.28
1.23. Определить токи в ветвях электрической цепи, схема которой показана на рис. 1.29. Параметры элементов цепи: Е =40 В, R1=2 Ом, RВН1=3 Ом, R2=10 Ом, R3=6 Ом, R4=8 Ом, R5=5 Ом, R6=3 Ом.
Рис. 1.29
Решение. Схема содержит 3 узла, 5 ветвей и один источник ЭДС. Указываем на схеме положительные направления токов в ветвях. Величина ЭДС задана, поэтому первоначально определим ток в ветви с источником. Задачу будем решать методом эквивалентных преобразований, используя только закон Ома.
Найдем сопротивление пятой ветви, содержащей последовательно соединенные резисторы R5 и R6 (рис. 1.29):
Пятая и четвертая ветви подключены к одной паре узлов, т.е. соединены параллельно, поэтому их эквивалентное сопротивление, найденное относительно зажимов 2-3:
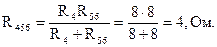
Сопротивление третьей ветви и найденное сопротивление R456 соединены последовательно (рис.1.30, а):
а)
б) в)
Рис. 1.30
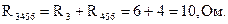
Относительно зажимов 1-3 сопротивление второй ветви и сопротивление R3456 соединены параллельно (рис. 1.30, б):
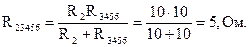
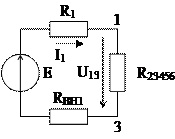
Относительно зажимов источника ЭДС сопротивление R23456 и сопротивления первой ветви соединены последовательно (рис. 1.30, в), поэтому входное сопротивление:
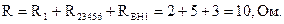
Ток ветви, содержащей источник ЭДС, определяем по закону Ома:
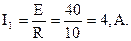
Для определения токов, выходящих из узла (1) рис. 1.29, записываем закон Ома для участка 1-3 схемы в рис. 1.30 и определяем напряжение между зажимами 1-3, используя уже вычисленное значение тока I1:
Используя закон Ома для того же участка в схеме б рис. 1.30, находим токи второй и третьей ветвей:
.
Для определения токов, выходящих из узла (2) рис. 1.29, используя закон Ома для участка 2-3 схемы а рис. 1.30, вычисляем напряжение между зажимами 2-3:
Далее, записав закон Ома для того же участка, но используя рис.1.29, определяем оставшиеся токи:
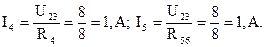
1.24. Определить для схемы рис. 1.31:
1) ток в сопротивлении 40 Ом, если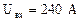 
;
2) напряжение на зажимах источника, если ток в сопротивление 8 Ом равен 1 А.
1.25. Определить токи во всех ветвях схемы рис. 1.32, если напряжение питания равно 30 В.
Рис. 1.31
Рис. 1.32
1.26. Определить напряжение питания схемы задачи 1.25, если значение тока I =1 А.
Законы Кирхгофа. Первый закон Кирхгофа применяют к узлу цепи и формулируют следующим образом:
алгебраическая сумма токов в узле равна нулю: SIk = 0.
При записи все токи, подходящие к узлу, можно считать положительными, а уходящие от узла – отрицательными, или наоборот.
Второй закон Кирхгофа:
а) для контуров, не содержащих источников ЭДС:
алгебраическая сумма напряжений вдоль участков замкнутого контура электрической цепи равна нулю:SUk = 0.
б) для контуров, в состав которых входят источники ЭДС:
алгебраическая сумма напряжений на резистивных элементах замкнутого контура равна алгебраической сумме ЭДС, входящих в этот контур:SURk = SEk или SR kIk = SEk.
При составлении уравнений по второму закону Кирхгофа необходимо произвольно выбрать направление обхода контура, для которого записывается уравнение.
Слагаемые берут со знаком «плюс» в случае, если направление обхода контура совпадает с направлением напряжения или ЭДС, в противном случае слагаемые берут со знаком «минус». Направление напряжения и тока на резисторе всегда совпадают.
1.27. В схеме рис. 1.33, имеющей параметры R1= 5 Ом; R2= 20 Ом; R3=R4= 10 Ом; E=30 В, определить напряжение Uab.
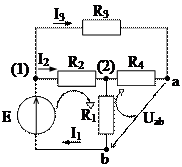
Рис. 1.33
Решение. В схеме два узла, три ветви и один источник.
Величина ЭДС известна. Применяя метод эквивалентных преобразований, найдем эквивалентное сопротивление участка цепи относительно зажимов 1-2:
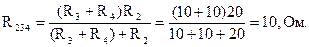
Эквивалентное сопротивление цепи:
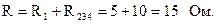
Ток в ветви с источником:
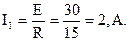
Ток второй ветви определяем с помощью второго закона Кирхгофа, составленного для контура, образованного первой и второй ветвями:
.
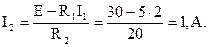
Ток третьей ветви вычисляем с помощью первого закона Кирхгофа: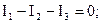 
Тогда 
Для определения напряжения между точками a и b, составим уравнение по второму закону Кирхгофа, мысленно замыкая контур a-2-b:
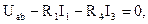откуда
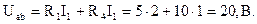
1.28. Определите показание амперметра при разомкнутом и замкнутом выключателе (рис. 1.34), дано: U = 48 B; R1 = 3 Ом; R2 = 9 Ом; R3 = 6 Ом; R4 = 18 Ом.
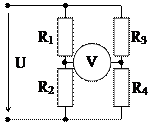
Рис. 1.34 Рис. 1.35
1.29. Определите показание вольтметра (рис. 1.35), считая сопротивление вольтметра бесконечно большим, если: U = 120 В; R1 = R2 = 20 Ом; R3 = 40 Ом; R4 = 20 Ом.
1.30. Определите показание вольтметра при разомкнутом и замкнутом выключателе SA (рис. 1.36). Сопротивление вольтметра считать бесконечно большим. Дано: E=90 B; U = 170 B; R1=10 Ом; R2=20 Ом; R3=30 Ом; R4 = 15 Ом.
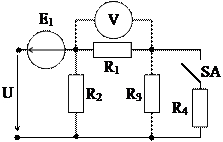
Рис. 1.36
1.31. Определить токи в ветвях цепи (рис. 1.37). Параметры сопротивлений указаны в Омах на схеме. ЭДС источника Е1 = 100 В.
Рис. 1.37 Рис. 1.38
1.32. Определить ток, на который рассчитаны провода, подводящие питание к приёмнику, характеризуемому сопротивлением R4 (рис. 1.38), если U = 12,5 В, R1 = R5 = 0,5 Ом, R2 = 0,8 Ом, R3 = 4 Ом, R4 = 0,4 Ом.
1.33. В цепи (рис. 1.39) амперметр показывает 8 А. Известные параметры сопротивлений и источников указаны на рисунке. Определить остальные токи.
1.34. На рис. 1.40 изображена схема включения двух электрических машин. Известны потенциалы узлов: φa= 0 В;φb = 120 B; φc = 95 B; φd = 100 B. Найти ЭДС каждой из машин и отдаваемую или потребляемую ими мощность.
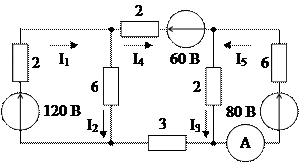
Рис. 1.39
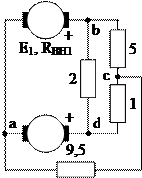
Рис. 1.40
Баланс мощностей
Баланс мощностей является следствием закона сохранения энергии и записывается следующим образом:
где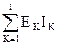 
- мощность, генерируемая источниками ЭДС;
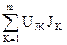- мощность, генерируемая источниками тока;
- мощность, рассеиваемая в резисторах.
Мощность, рассеиваемая в резисторах, всегда положительна. Мощность источников энергии может быть как положительной, так и отрицательной. Отрицательный знак мощности означает, что соответствующий источник работает в режиме потребления электрической энергии. Выполнение баланса мощностей является одним из критериев правильности расчета электрической цепи.
1.35. Рассчитать мощности приемников и источников электрической энергии и проверить выполнение баланса мощностей для электрической цепи, приведенной в задаче 1.33.
1.36. Мощность, отдаваемая источником, 48 Вт; мощность внутренних потерь - 1,2Вт. Какой величиной ЭДС должна обладать батарея, чтобы напряжение на зажимах приемника UН было равным 24 В (рис. 1.41)?
Рис. 1.41
1.37. Мощность, выделяемая в резисторе R4 - P4 = 475,26 Вт. Какой мощностью обладает источник электрической энергии и при каком напряжении источника питания работает цепь (рис.1.42), если: R1 = R2 = 0,5 Ом, R3 = R4 = 6 Ом, R5 = R6 = 1 Ом, R7 = 2 Ом.
Рис. 1.42
Метод законов Кирхгофа
Метод является универсальным и используется для расчета значений токов в ветвях электрической цепи по известным значениям ЭДС и токов источников электрической энергии и сопротивлений элементов цепи.
Алгоритм расчета:
1. Определяют количество узлов в схеме, число ветвей, в том числе, число ветвей с неизвестными токами.
2. Показывают условно-положительные направления токов в ветвях расчетной схемы, а также указывают условно-положительные направления напряжений на всех элементах электрической цепи.
3. Составляют систему уравнений по законам Кирхгофа.
Общее число уравнений, которое необходимо записать на основании законов Кирхгофа равно числу ветвей с неизвестными токами. Для расчета токов в цепи, содержащей “ в ” ветвей с неизвестными токами составляют систему из “ в ” уравнений. По первому закону Кирхгофа число уравнений на одно меньше числа узлов цепи. Остальные уравнения записывают по второму закону Кирхгофа.
4. Решают систему уравнений и определяют неизвестные токи.
5. Для проверки правильности расчета составляют уравнение баланса мощностей.
1.38. Определите ток в цепи (рис.1.43) методом законов Кирхгофа. Дано: E1=100 B; E2=40 B; E3=60 B; R01=0,5 Ом; R1=3,5 Ом; R2=16 Ом; R3=1,8 Ом; R4=8 Ом; R5=4 Ом; R6=6 Ом; R03=0,2 Ом.
Решение. В схеме два узла (у=3), три ветви с неизвестными токами (в=3) и три источника электрической энергии, расположенных в разных ветвях схемы.
Обозначим на схеме условные положительные направления токов. Общее число уравнений, которые необходимо составить по двум законам Кирхгофа равно трем: по первому закону у-1=2-1=1 уравнение и по второму закону в-(у-1)=3-(2-1)=2 уравнения.
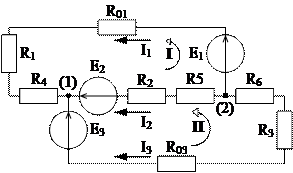
Рис. 1.43
Запишем уравнения цепи в матричной форме:
I1 + I2 + I3 =0;
I1 (R01+R1+R4) - I2 (R2+R5) =E1-E2;
I2 (R2+R5) - I3 (R03+R3+R6) =E2-E3.
Токи ветвей находим методом определителей:
; 
; 
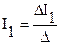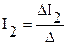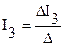
где главный определитель:
и частные определители:
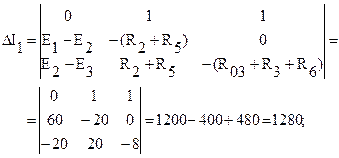
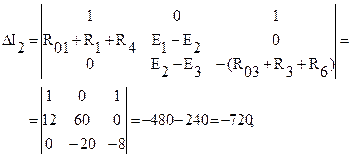
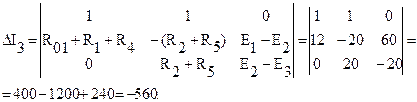
Находим токи ветвей:
Правильность расчетов можно проверить и с помощью исходной системы уравнений. Например, по первому закону Кирхгофа: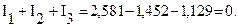 
Токи I2, I3 отрицательны, следовательно, их истинные направления противоположны первоначально выбранным направлениям. Но исправления вносить на схеме не следует.
1.39. Для схемы рис. 1.44 определить токи в ветвях, если E1=120 В, J2=5 А, R1=40 Ом, R2=20 Ом, R3=25 Ом, R4=50 Ом.
☻ Схема рис. 1.44 состоит из четырех ветвей с неизвестными токами (в=4) и одной ветви с источником тока, величина тока которого известна. Ветви соединены в трех узлах (у=3). Ветвь с идеальным источником тока обладает бесконечно большим сопротивлением, поэтому в образовании контуров не участвует.
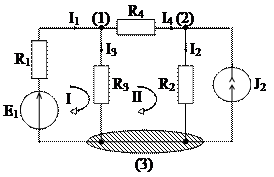
Рис. 1.44
Составляем систему из четырех уравнений (в=4), в которой число уравнений по первому закону Кирхгофа: у-1=3-1=2; по второму закону - в-(у-1)=4-(3-1)=2:
для узла a: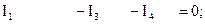 
для узла b: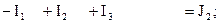 
для контура I: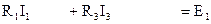 
;
для контура II: 
Из нее вычисляем неизвестные токи.
1.40. В схеме рис. 1.45 определите токи в ветвях и показание вольтметра. Дано: Е1=110 В; Е2=40 В; Е3=220 В; Rвн1=0,2 Ом; Rвн2=0,3 Ом; R1=30 Ом; R2=20 Ом; R3=70 Ом; R4=60 Ом; R5=40 Ом.
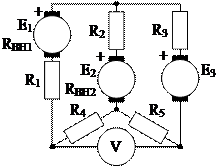
Рис. 1.45
Метод узловых потенциалов
На практике всегда стремятся сократить число уравнений, подлежащих решению. Эффективным методом для этого является метод узловых потенциалов.
Этот метод основан на применении только первого закона Кирхгофа и закона Ома. Ток в любой ветви электрической цепи определяется разностью потенциалов между концами ветви, поэтому за неизвестные принимают потенциалы узлов.
Один из узлов заземляют, принимая его потенциал равным нулю, а потенциалы остальных узлов рассчитывают относительно него. Число уравнений равно числу неизвестных потенциалов, т.е. у-1.
Согласно этому методу потенциал некоторого k-того узла φk, умноженный на алгебраическую сумму проводимостей ветвей, сходящихся в этом узле gkk за вычетом потенциалов соседних узлов, соединенных ветвями с k-м узлом, умноженные на проводимости этих ветвей, равен узловому току k-того узла Jkk. Узловой ток Jkk определяется алгебраической суммой токов, полученных от деления ЭДС ветвей, подходящих к k-тому узлу на сопротивления данных ветвей ∑Ekgk и токов источников тока ∑Jk. Если ЭДС или ток источника тока направлены к узлу, то они принимаются со знаком «плюс», если от узла - то со знаком «минус».
1.41. Используя данные задачи 1.39, определить токи в ветвях схема рис. 1.44.
☻ В схеме 3 узла.Принявφ3=0 В, необходимо записать еще два уравнения - для определения потенциалов узлов (1) и (2). В общем виде уравнения будут выглядеть так:
для первого узла: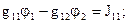 
для второго узла: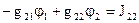 
,
где g11 и g22 - сумма проводимостей ветвей, присоединенных к узлам (1) и (2); g12=g21 - сумма проводимостей ветвей, соединяющих эти узлы.
При записи численных значений проводимостей следует оставлять 6 знаков после запятой.
J11 и J22 – узловые токи первого и второго узлов, вычисляемые по формуле:
, 
.
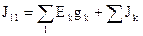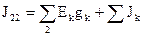Уравнения цепи для вычисления потенциалов узлов схемы рис. 1.44 будут выглядеть так:
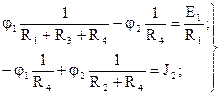
Далее, используя вычисленные потенциалы узлов (1), (2) и φ3=0, следует определить токи в ветвях согласно закону Ома:
,
где φa, φb – потенциалы узлов, к которым подключена ветвь с искомым током, при этом ток ветви направлен из узла a в узел b;
Е – ЭДС ветви, которая записывается со знаком «плюс», если ее направление совпадает с направлением искомого тока или со знаком «минус», если не совпадает;
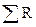- сумма сопротивлений ветви.
Токи в ветвях схемы рис. 1.44 можно записать как:
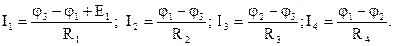
Если сравнить между собой методы определения токов в рассматриваемой цепи (рис. 1.44), то наиболее целесообразным окажется метод узловых потенциалов, так как для расчета
токов этим методом необходимо решить систему уравнений всего лишь второго порядка. Расхождения в результатах расчета токов в одной схеме различными методами объясняется погрешностями, возникающими в результате округлений.
1.42. Определить ток в диагонали моста (рис. 1. 46), если E=30 В, R1=120 Ом; R2=30 Ом; R3= 60 Ом; R4=60 Ом; R5=90 Ом.
Рис. 1.46
1.43. Определить показания вольтметра в цепи (рис. 1.47).
1.44. В схеме (рис. 1.47) вместо вольтметра включили амперметр. определить его показания.
Рис.1.47
Метод двух узлов
Метод двух узлов является частным случаем метода узловых потенциалов (МУП).
Как и в МУП потенциал одного из узлов заземляют (например, j2=0 В), тогда потенциал другого узла, умноженный на сумму проводимостей ветвей, сходящихся в этом узле, равен узловому току этого узла. В общем виде: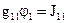 
. Узловой ток определяют аналогично МУП: 
В общем виде потенциал первого узла можно определить как:
,
где 
- алгебраическая сумма условных узловых токов, создаваемых ЭДС и источниками тока, подходящих к узлу k;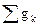 
- сумма проводимостей ветвей, подходящих к этому узлу.
1.45. По данным задачи 1.38 определите токи в цепи (рис.1.43) методом узловых потенциалов.
Решение. Пустьj2=0 В. Записываем уравнение цепи для определения потенциала узла 1:
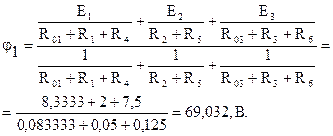
Токи в ветвях
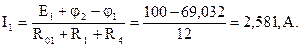
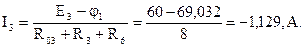
Проверка: I1+I2+I3=2,581-1,452-1,129=0, A.
Погрешность обусловлена точностью расчета. Величина погрешности d<3%, что допустимо.
1.46. Определите режимы работы источников ЭДС Е1, Е3 и показания амперметров в цепи (рис. 1.47).
Дано: Е1=36 В; Е3=24 В; R01=0,1 Ом; R2=12 Ом. Сопротивления амперметров равны нулю.
Рис. 1.48
1.47. Определит токи в ветвях схемы (рис.1.49).
1.48. В цепи (рис. 1.50) определить ЭДС Е и токи I1 и I2.
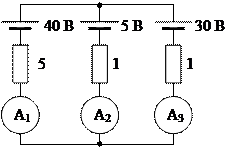
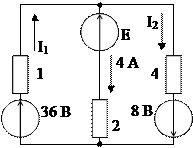
Рис. 1.49 Рис. 1.50
Метод наложения
Метод наложения облегчает расчет электрической цепи, находящейся под воздействием нескольких источников электрической энергии.
При расчетах методом наложения в схеме оставляют один источник, остальные источники удаляют, сохраняя внутренние сопротивления и проводимости. Зажимы удаленных источников ЭДС замыкают накоротко, источников тока - оставляют свободными. Далее определяют напряжения и токи ветвей в полученной простой схеме. По завершении расчетов всех простых схем вычисляют алгебраическую сумму найденных напряжений и токов.
1.49. Рассчитать токи в ветвях электрической цепи, схема которой показана на рис. 1.51, используя метод наложения.
Дано: E1 =24 В, E2 =96 В, E3 =48 В, R1 = 8 Ом, R 2 = 16 Ом, R 3 = 8 Ом, R 4 = 16 Ом.
Решение. В схеме рис. 1.51 три узла, пять ветвей с неизвестными токами и три источника ЭДС, расположенных в разных ветвях схемы. Выбираем произвольно положительные направления токов в ветвях исходной схемы (рис. 1.51).
Затем разделим сложную схему (рис. 1.51) на три схемы, в каждой из которых оставим по одному источнику, исключив остальные, но сохранив их внутренние сопротивления (рис. 1.52, а, б, в).
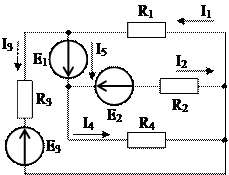
Рис. 1.51
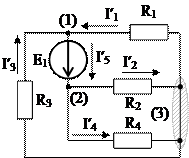
а) б)
в)
Рис. 1.52
Так как цепь содержит только идеальные источники ЭДС, внутреннее сопротивление которых равно нулю, то заменим источники ЭДС короткозамкнутыми участками (рис. 1.52, а, б, в).Каждая из полученных схем содержит один источник энергии, поэтому в ней можно сразу правильно показать положительные направления частичных токов.
Токи в полученных схемах будем определять методом эквивалентных преобразований.
Определим частичные токи от действия первого источника ЭДС Е1 (рис.1.52, а). В этой схеме три узла, пять ветвей с неизвестными токами. Вторая и четвертая ветви соединены параллельно относительно узлов (2) и (3) и эквивалентное сопротивление этих ветвей будет равно:
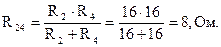
Первая и третья ветви так же соединены параллельно относительно узлов (3) и (1), и их эквивалентное сопротивление найдем как:
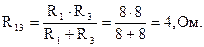
Полученные сопротивления R13 и R24 соединены между собой последовательно, поэтому эквивалентное сопротивление относительно зажимов источника:
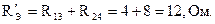
Ток в ветви с источником ЭДС E1: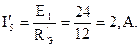 
Напряжение между узлами (2) и (3):
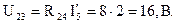
Частичные токи второй и четвертой ветвей:
Напряжение между узлами (3) и (1):
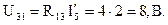
Частичные токи первой и третьей ветвей:
Определим частичные токи от действия второго источника ЭДС Е2 (рис.1.52, б).
В рассматриваемой схеме два узла. Первая, третья и четвертая ветви присоединены к этим узлам, т.е. соединены параллельно:
Полученное сопротивление включено последовательно с сопротивлением второй ветви. Эквивалентное сопротивление схемы:
.
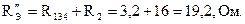Ток в ветви с источником: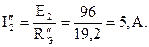 
Напряжение на параллельных ветвях:
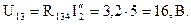
Токи в параллельных ветвях:
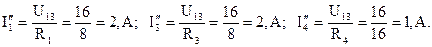
Ток I′′5 можно рассчитать, используя первый закон Кирхгофа:
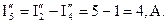
Определим частичные токи от действия третьего источника ЭДС Е3 (рис.1.52, в). В схеме два узла, к которым подключены первая, вторая и четвертая ветви, т.е. они соединены параллельно и их эквивалентное сопротивление равно:
Полученное сопротивление соединено последовательно с сопротивлением третьей ветви. Эквивалентное сопротивление всей схемы:
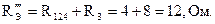
Ток в ветви с источником ЭДС:
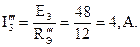
Напряжение между узлами:
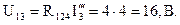
Токи в параллельных ветвях:
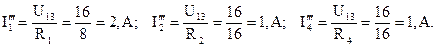Ток I′′5 можно определяем из первого закона Кирхгофа:
Потенциальная диаграмма
Для оценки напряжения между различными точками схемы полезны потенциальные диаграммы. Они представляют собой графическое изображение распределения потенциалов вдоль какого-либо участка схемы или замкнутого контура электрической цепи, причем каждой точке схемы соответствует определенная точка на диаграмме.
Точке отсчета, потенциал которой принят равным нулю, на диаграмме соответствует начало координат. По осиабсцисс (ось x) последовательно откладывают сопротивления в порядке их следования по выбранному направлению обхода контура, а по оси ординат (ось у) откладывают потенциалы точек контура.
1.50. Для схемы рис. 1.53 экспериментально были получены величины ЭДС источников электрической энергии (E1=135 В, E2=90 В), их внутренних сопротивлений (RВН1=1 Ом, RВН2=2 Ом), потенциалы узлов: φa= 0 В; φb = 120 B; φc = 95 B; φd = 100 B, величины токов в ветвях с источниками энергии (I1=15 А и I2=5 А) и сопротивления пассивных элементов (указаны на схеме в омах). По экспериментальным данным постройте потенциальную диаграмму по контуру a, b, c, d, a, определите режимы работы источников.
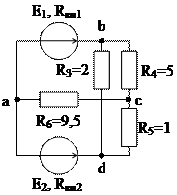
Рис. 1.53
Решение. Для схемы рис. 1.53 контур был уже выбран и разбит на отдельные элементы, потенциалы точек контура известны. Обходить рассматриваемый контур будем по ходу часовой стрелке. Точкой отсчета является точка a, потенциал которой равен нулю.
Сопротивление всего контура получаем как арифметическая сумма всех сопротивлений, вошедших в рассматриваемый контур: 
Минимальное значение потенциал принимает в точке а (φa= 0 В), а максимальное значения – в точке b (φb = 120 B). Выбираем масштабы: по оси абсцисс – 1 Ом/см, а по оси ординат – 20 В/см.
Далее откладываем сопротивления участков порядке их следования (RВН1→ R4→ R5→ RВН2), а по оси ординат откладывают потенциалы точек (a→b→c→d→a).
На рис. 1.54 приведена потенциальная диаграмма для контура a→b→c→d→a схемы рис. 1.53.
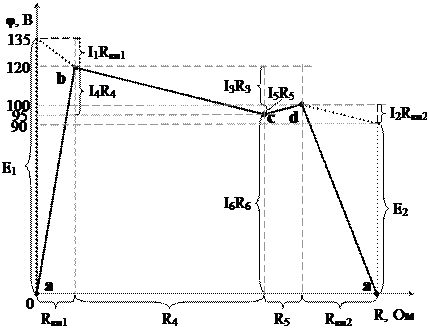
Рис. 1.54
1.51. Для участка цепи рис. 1.55 постройте потенциальную диаграмму. ЭДС источников и сопротивления резисторов даны на схеме.
Рис. 1.55
