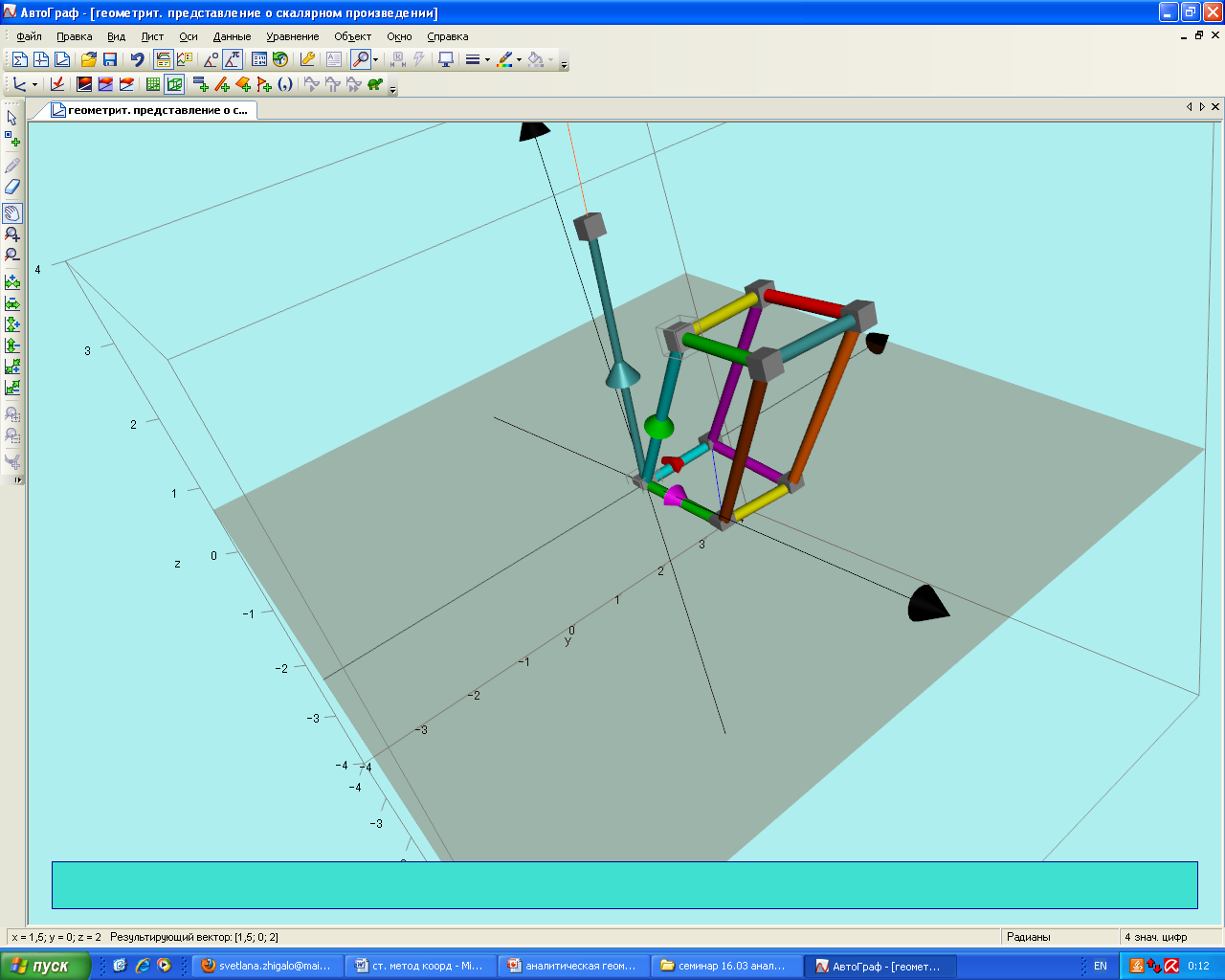
 т.к. площадь параллелограмма – произведение двух сторон на Sina- между ними – это модуль векторного
т.к. площадь параллелограмма – произведение двух сторон на Sina- между ними – это модуль векторного
произведения.
 - это расстояние от конца вектора с до плоскости векторов а и в.
- это расстояние от конца вектора с до плоскости векторов а и в.
 дает
дает  объем параллелипипеда, построенного на этих трех векторах.
объем параллелипипеда, построенного на этих трех векторах.
 числение смешанного произведения.
числение смешанного произведения.
Результат векторного произведения (формула 1) умножаем скалярно на вектор  .
.

Уравнение плоскости./вывод/
Если  , то вектора
, то вектора  будут компланарны.
будут компланарны.
 Три ненулевых вектора компланарны, если их смешанное произведение равно нулю.т.к
Три ненулевых вектора компланарны, если их смешанное произведение равно нулю.т.к
1. Если два из трех вектора коллиниарны (тогда sina=0), то три вектора компланарны.
2. 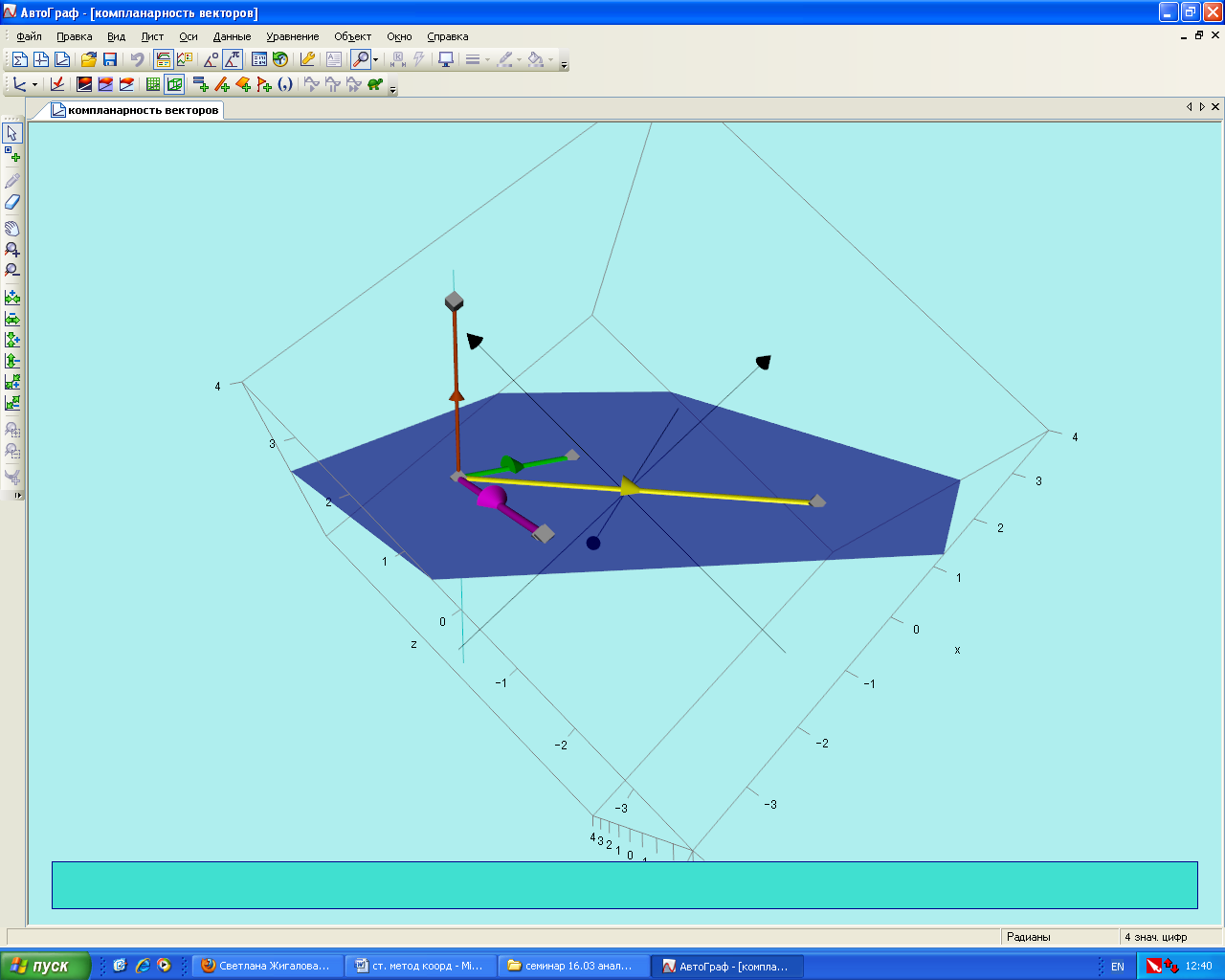 Если Cosb=0, то <в=90*, тогда вектор перпендикулярен к нормали к плоскости, образованной векторами
Если Cosb=0, то <в=90*, тогда вектор перпендикулярен к нормали к плоскости, образованной векторами  , т.е вектор с лежит в плоскости векторов
, т.е вектор с лежит в плоскости векторов 

Вектор  ,
,  - координаты конкретной точки, лежащей в плоскости.
- координаты конкретной точки, лежащей в плоскости.

 ,
,  ,
, 

Уравнение плоскости имеет вид: 
Заметим, что если дано уравнение плоскости, то нам известны координаты нормали.
 Расстояние от точки до плоскости
Расстояние от точки до плоскости
| М |
| Е |
| К |
 исходная точка. KN- нормаль, точка Е
исходная точка. KN- нормаль, точка Е  произвольная точка плоскости.
произвольная точка плоскости.
| N |
Используем скалярное произведение векторов. 
Расстояние от точки М до плоскости: 
 - вектор нормали.
- вектор нормали.
Получаем формулу:d=  .преобразуем,
.преобразуем,
d=  т.к. точка Е принадлежит плоскости, то её координаты обращают уравнение плоскости в верное равенство.
т.к. точка Е принадлежит плоскости, то её координаты обращают уравнение плоскости в верное равенство.


 Задачи:
Задачи:
3. (из ЕГЭ) В единичном кубе АВСDА1В1С1D1найти расстояние от точки С1 до плоскости АВ1С
4. 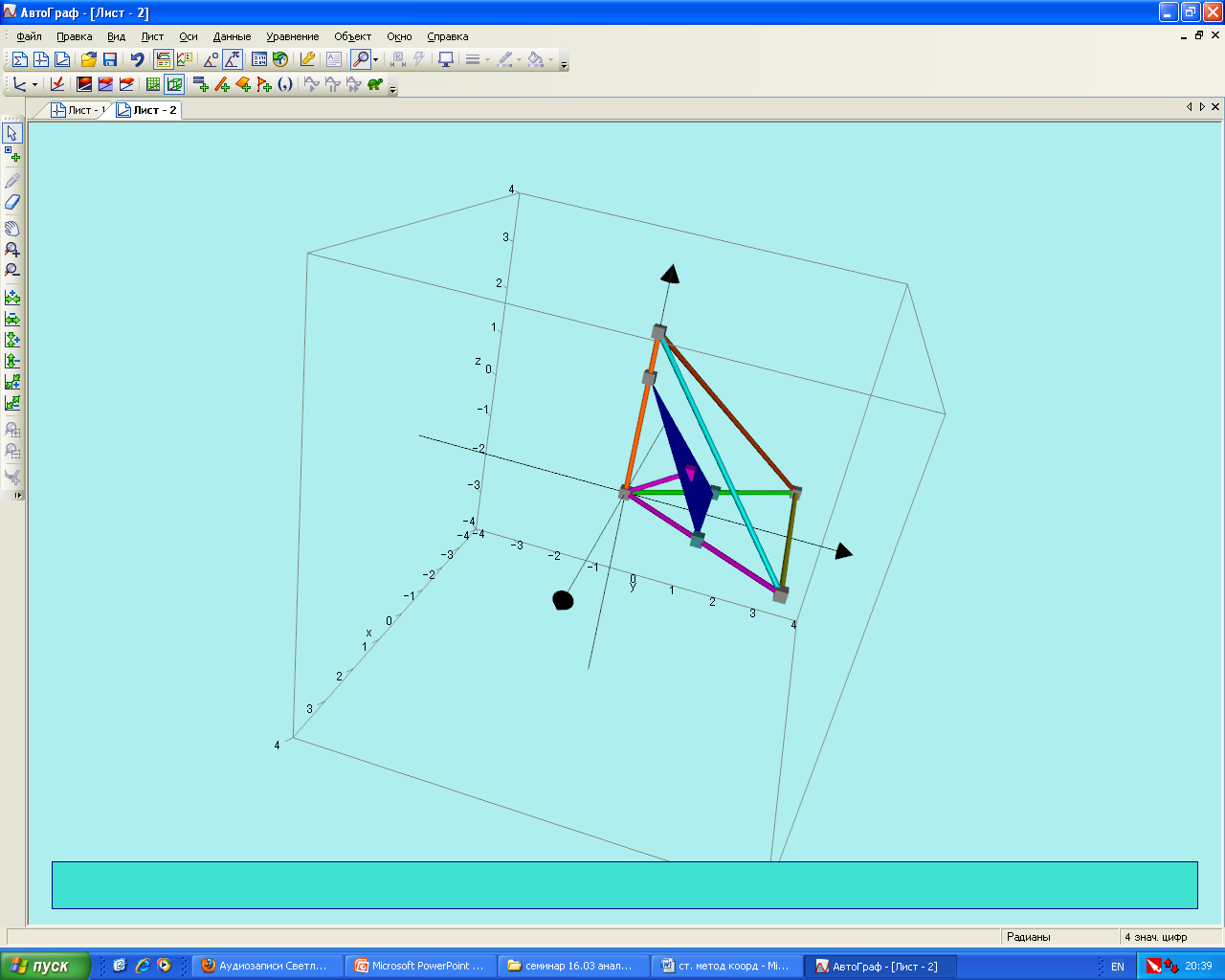 (из ЕГЭ)Ребро АD пирамиды АВСD- перпендикулярно плоскости основания. Найти расстояние от вершины А до плоскости ЕМК, где Е и М – середины ребер АВ, АС, АК:КD=3:1.АD=4, АВ=АС=5, ВС=6
(из ЕГЭ)Ребро АD пирамиды АВСD- перпендикулярно плоскости основания. Найти расстояние от вершины А до плоскости ЕМК, где Е и М – середины ребер АВ, АС, АК:КD=3:1.АD=4, АВ=АС=5, ВС=6
Задачи:
1. Найдите острый угол между плоскостями 2х-у-3z+5=0 и х+у-2=0.
2. Составить уравнение плоскости:
a. Которая проходит через точку М(2,1,-1) и имеет нормальный вектор п(1,-2,3)
b. Проходит через точку М(3.-1,2) и перпендикулярно вектору МК, К(4,-2,-1)
3. Установить компланарны ли вектора а(2,3,-1),в(1.-1,3),с(1,9,-11)
4. Даны точки А(1,0,1),В(-2,2,1),С(2,0,3). Найдите уравнение плоскости АВС.
5. Даны точки А(1,0,1),В(-2,2,1),С(2,0,3) и D(0,4,-2). Найдите острый угол между плоскостями АВС и ВСD.
6. Даны точки А(1,0,1),В(-2,2,1),С(2,0,3) и D(0,4,-2). Найдите расстояние от точки D до плоскости АВС.
7. Дан параллелепипед А(1,2.3), В(9,6.4), D(3,0,4) А1(5,2,6).Вычислить
a. Объем параллелепипеда
b. Угол между АС1 и плоскостью (АВС)
Задания из ЕГЭ
1. В кубе АВСDА1В1С1D1, плоскость Р проходит через диагональ А1С1 и середину ребра DD1. Найдите расстояние от середины ребра СD до плоскости Р, если ребро куба равно 4.
2. В кубе АВСDА1В1С1D1 найдите тангенс угла между прямой ВС и плоскостью, проходящей через точки А1,D и М- середину грани А1В1С1D1.
3. В правильной треугольной призме АВСА1В1С1 АА1=1,АВ=1,M и N середины граней ВВ1СС1(пересечение диагоналей) и А1В1С(точка пересечения медиан). Найти угол между прямой MN и плоскостью ВВ1С1
4. В правильной четырех угольной пирамиде SАВСD, все ребра которой равны 1, найдите косинус угла между прямой АВ и плоскостью SАD.
5. Стороны основания правильной треугольной пирамиды SАВС равна 6, а боковое ребро равно  . найти синус угла между основанием АВС и отрезком, соединяющим середины ребер SС и АВ.
. найти синус угла между основанием АВС и отрезком, соединяющим середины ребер SС и АВ.
6. В правильной шестиугольной пирамиде SA…F боковые ребра равны 2, а стороны основания 1. Найдите косинус угла между прямой АС и плоскостью SAF
Задания для домашней работы:
1. Даны точки А(-3,0,1) В (2,1,-1),С(-2,2,0) и D(1,3,2)
Найдите:
· Уравнение плоскости АВС.
· Острый угол между плоскостями АВС и ВСD.
· Расстояние от точки D до плоскости АВС.
7. В кубе АВСDА1В1С1D1, плоскость Р проходит через А1,С и середину ребра DС1. Найдите расстояние от вершины D1 до плоскости Р, если ребро куба равно 6.
 Уравнение прямой в пространстве. Расстояние от точки до прямой.
Уравнение прямой в пространстве. Расстояние от точки до прямой.
В прямоугольном параллелепипеде АВСDА1В1С1D1, АD=4, АВ=2, АА1=6. Найти расстояние от точки А до прямой ЕК, Где ЕD:ЕD1=1:5, К- Середина отрезка С1В1.
Решение. АМ расстояние от точки А до прямой ЕК. А(0,0,0),D(4,0,0), Е(4,0,1),К(2,2,6) М(х,у,z),  вектора ЕМ и ЕК коллиниарны,
вектора ЕМ и ЕК коллиниарны, 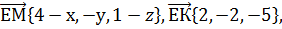
 =t
=t






