— для серого тела
6, Импульс фотона рg получим, если в общей формуле теории относительности положим массу покоя фотона 
= 0: 
7, Соотношение неопределенностей имеет вид (в проекциях на координатные оси):
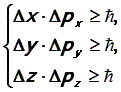
| (16) |
где 
Соотношение неопределенностей определяет допустимый принципиальный предел неточностей координат D x, D y, D z и значений проекций импульсов D px, D py, D pz, которые характеризуют состояние микрочастицы. Чем точнее определена координата x (малое значение D x), тем с меньшей точностью возможно охарактеризовать проекцию импульса px(большое значение D px), и наоборот.
8, 
10, Так, интерференция возникает при разделении первоначального луча света на два луча при его прохождении через тонкую плёнку, например плёнку, наносимую на поверхность линз у просветлённых объективов. Луч света, проходя через плёнку толщиной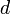 
, отразится дважды — от внутренней и наружной её поверхностей. Отражённые лучи будут иметь постоянную разность фаз, равную удвоенной толщине плёнки, от чего лучи становятся когерентными и будут интерферировать. Полное гашение лучей произойдет при 
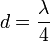, где 
— длина волны. Если 
нм, то толщина плёнки равняется 550:4=137,5 нм.
Лучи соседних участков спектра по обе стороны от нм интерферируют не полностью и только ослабляются, отчего плёнка приобретает окраску. В приближении геометрической оптики, когда есть смысл говорить об оптической разности ходалучей, для двух лучей
— условие максимума;
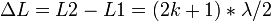— условие минимума,
где k=0,1,2... и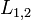 
— оптическая длина пути первого и второго луча, соответственно.
11, Статистика Фе́рми — Дира́ка в статистической физике — квантовая статистика, применяемая к системам тождественных фермионов (как правило, частиц с полуцелым спином, подчиняющихся принципу запрета Паули, то есть, одно и то же квантовое состояние не может занимать более одной частицы); определяет распределение вероятностей нахождения фермионов на энергетических уровнях системы, находящейся в термодинамическом равновесии; В статистике Ферми — Дирака среднее число частиц в состоянии с энергией 
есть
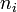— среднее число частиц в состоянии 
, — энергия состояния , 
— кратность вырождения состояния (число состояний с энергией ), 
— химический потенциал (который равен энергии Ферми 
при абсолютном нуле температуры), 
— постоянная Больцмана,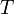 
— абсолютная температура.
В статистической механике статистика Бо́зе — Эйнште́йна определяет распределение тождественных частиц с нулевым или целочисленнымспином (таковыми являются, например, фотоны и атомы гелия-4) по энергетическим уровням в состоянии термодинамического равновесия Согласно статистике Бозе — Эйнштейна, количество частиц в заданном состоянии i, равняется
где 
, ni — количество частиц в состоянии i, gi — вырождение уровня i, εi — энергия состояния i, μ — химпотенциал системы, k — постоянная Больцмана, T — абсолютное значение температуры.
В пределе 
статистика Бозе-Эйнштейна переходит в статистику Максвелла — Больцмана, а в пределе 
— в распределение Рэлея:
.
Билет 18
Поперечность электромагнитной волны является одним из самых важных ее свойств. В силу поперечности электромагнитной волны световой вектор всегда перпендикулярен к направлению распространения волны. В бегущей плоской электромагнитной волне векторы напряженности E электрического поля и индукции B магнитного поля в каждой точке и в каждый момент времени образуют с волновым вектором k (совпадает с направлением распространения волны) правую тройку векторов (рис. 1) В этом заключается свойство поперечности электромагнитных волн. Поперечность электромагнитной волны лишает ее осевой симметрии относительно направления ее распространения из-за наличия выделенных направлений (векторов E и B).
2, Скорость распространения волны 
, входящая в волновое уравнение, есть скорость перемещения в пространстве фиксированного значения фазы волны, в связи с чем ее называют фазовой скоростью. Эту скорость легко определить, взяв дифференциал от произвольного постоянного значения фазы ωt – kx+ α = const. После чего находим:
3.Условие максимума освещенности при интерференции:
, где k = 2 m – четное число;
условие минимума освещенности при интерференции:
, где k = 2 m + 1 – нечетное число,
Δ – оптическая разность хода двух лучей (м); λ – длина волны (м); m – некоторое целое число (m = 0, ±1, ±2, …).
Условие максимума освещенности при интерференции:
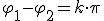, где k = 2 m – четное число;
условие минимума освещенности при интерференции:
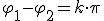, где k = 2 m + 1 – нечетное число,
φ 1 - φ 2 – разность фаз колебаний (рад); m – некоторое целое число (m = 0, ±1, ±2, …).
4. Закон Малюса — зависимость интенсивности линейно-поляризованного света после его прохождения через поляризатор от угла 
между плоскостями поляризации падающего света и поляризатора.
где I0 — интенсивность падающего на поляризатор света, I — интенсивность света, выходящего из поляризатора, ka - коэффициент прозрачности анализатора.
5. уравнение Шрёдингера запишется в виде:
где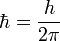 
, 
— постоянная Планка; 
— масса частицы, 
— внешняя по отношению к частице потенциальная энергия в точке 
, 
— оператор Лапласа (или лапласиан), эквивалентен квадрату оператора набла и в n-мерной системе координат имеет вид:
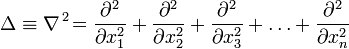
6.
7. Вы́нужденное излуче́ние, индуци́рованное излучение — генерация нового фотона при переходе квантовой системы (атома, молекулы, ядра и т. д.) из возбуждённого в стабильное состояние (меньший энергетический уровень) под воздействием индуцирующего фотона, энергия которого была равна разности энергий уровней. Созданный фотон имеет ту же энергию, импульс, фазу и поляризацию, что и индуцирующий фотон (который при этом не поглощается). Оба фотона являются когерентными.Процесс испускания фотона возбужденным атомом (возбужденной микросистемой) без каких-либо внешних воздействий называется спонтанным (или самопроизвольным) излучением
8. При́нцип Па́ули (принцип запрета) — один из фундаментальных принципов квантовой механики, согласно которому два и более тождественных фермиона (частиц с полуцелым спином) не могут одновременно находиться в одном квантовом состоянии. Принцип Паули можно сформулировать следующим образом: в пределах одной квантовой системы в данном квантовом состоянии может находиться только одна частица, состояние другой должно отличаться хотя бы одним квантовым числом.
В статистической физике принцип Паули иногда формулируется в терминах чисел заполнения: в системе одинаковых частиц, описываемых антисимметричной волновой функцией, числа заполнения могут принимать лишь два значения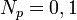 
10, Гармонической волной называется линейная монохроматическая волна, распространяющаяся в бесконечной динамической системе. В распределённых системах общий вид волны описывается выражением, являющимся аналитическим решением линейного волнового уравнения
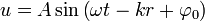
где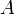 
– некоторая постоянная амплитуда волнового процесса, определяемая параметрами системы, частотой колебаний и амплитудой возмущающей силы; 
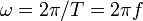– круговая частота волнового процесса, 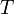– период гармонической волны, 
– частота; 
– волновое число, – длина волны, 
– скорость распространения волны;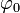 
– начальная фаза волнового процесса, определяемая в гармонической волне закономерностью воздействия внешнего возмущения.
Если искать решение для гармонической волны путём предельного перехода от соответствующих решений для динамических систем с сосредоточенными параметрами, то указанное выражение существенно уточнится, выявив связь, заложенную в амплитуду 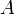. Это решение для амплитуды имеет вид
где,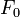 
– амплитуда воздействующей силы, 
– плотность распределённой упругой системы, 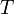– в данном случае, жёсткость линии с распределёнными параметрами
Электромагнитные волны поперечны – векторы и перпендикулярны друг другу и лежат в плоскости, перпендикулярной направлению распространения волны. Связь между значениями Е и Н. Запишем решение уравнения (3), а также решения аналогичных уравнений для других компонент полей, в виде
где f и g – произвольные функции. 
