Модуль к.ч.
Модулем числа  називається невід’ємне число
називається невід’ємне число  .
.
Модуль дійсного числа дорівнює його абсолютній величині. Справді, якщо 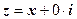 , то
, то  .
.
Приклади.
1)  .
.
2) 
3)  .
.
4) Показати, що модулі спряжених чисел рівні.
Розв¢язання. Досить обчислити модулі спряжених чисел



4.6. Додавання і віднімання к.ч.

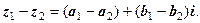
Приклади
1.  .
.
2.  .
.
Обчислити самостійно
1.  2.
2. 
3.  4.
4. 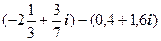
5.  6.
6. 
7.  8.
8. 
9.  10.
10. 
Відповіді. 1.  . 2.
. 2.  . 3.
. 3.  . 4.
. 4.  . 5.
. 5.  . 6.
. 6.  . 7.
. 7.  .
.
8.  . 9.
. 9.  . 10.
. 10.  .
.
Множення к.ч.
Множення к.ч. виконуємо згідно правила (вважаючи, що  ):
):


Приклади.

 .
.
Правильна тотожність 
 Дійсно,
Дійсно,

Спростити самостійно
1.  2.
2. 
3.  4.
4. 
5.  6.
6. 
7. 
Відповіді. 1.  . 2.
. 2.  . 3.
. 3.  . 4.
. 4.  . 5.
. 5.  .
.
6.  . 7.
. 7.  .
. 
4.8. Ділення к.ч.
Ділення к.ч. виконується згідно правила (при умові  ):
):


Приклади.
1) 

2) 
3) Розв’язати рівняння 
Розв’язання.  Відповідь:
Відповідь:  .
.
Перевірка: 
Спростити самостійно вирази
1.  2.
2.  3.
3.  .
.
Відповіді. 1.  . 2.
. 2.  . 3.
. 3.  .
.
Комплексне число як точка площини
У вибраній прямокутній системі координат число  зображається точкою
зображається точкою  (рис.1.1). Навпаки, якщо задана точка
(рис.1.1). Навпаки, якщо задана точка  , то їй співставляється к.ч.
, то їй співставляється к.ч.  . Таким чином, між множиною к.ч. і множиною точок площини (з заданою прямокутною системою координат) встановлюється взаємно однозначна відповідність.
. Таким чином, між множиною к.ч. і множиною точок площини (з заданою прямокутною системою координат) встановлюється взаємно однозначна відповідність.

Рис.1.1.
Очевидно, що дійсні числа зображуються точками на осі  , а чисто уявні - на осі
, а чисто уявні - на осі  ; з цієї причини
; з цієї причини  називають дійсною, а
називають дійсною, а  – уявною віссю; площину
– уявною віссю; площину  називають комплексною площиною, а к.ч. - точками цієї площини.
називають комплексною площиною, а к.ч. - точками цієї площини.
Приклади. Знайти множину к.ч., що задовольняють умову:
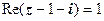 ;
;
 .
.
Розв’язання.
1) Нехай  . Умову перепишемо в рівносильній формі:
. Умову перепишемо в рівносильній формі: 
Відповідь: множина чисел  пряма
пряма 
2) Якщо  , то,
, то, 
 , отже,
, отже, 
Відповідь: множина чисел  - півплощина, що розміщена нижче прямої
- півплощина, що розміщена нижче прямої  .
.
Побудувати на площині ХОУ к.ч., записати їх дійсну та уявну частину. Обчислити модулі к.ч.
1.  . 2.
. 2.  . 3.
. 3. 
Відповіді. 1. 


2. 

 .
.
3. 

 .
.
4.10. Коло, круг, кільце
Нехай дано числа 
Рівнянню  задовольняють всі числа (і тільки вони), що розміщені на колі радіуса
задовольняють всі числа (і тільки вони), що розміщені на колі радіуса  з центром у точці
з центром у точці 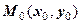 . Дійсно, якщо
. Дійсно, якщо  , то
, то 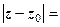

 .
.
Очевидно, що нерівності  і
і  задають відповідно круг і кільце. На рис. 1.2 зображено кільце
задають відповідно круг і кільце. На рис. 1.2 зображено кільце  з центром у точці
з центром у точці  .
.
Звернемо увагу на вироджені випадки кільця  :
:
(1)  – круг з виключеним центром
– круг з виключеним центром  ;
;
(2)  – зовнішність круга
– зовнішність круга  – круг з границею;
– круг з границею;
(3)  – вся площина з виключеною точкою
– вся площина з виключеною точкою  ;
;
(4) при  маємо пусту множину.
маємо пусту множину.

Рис. 1.2
Приклад. З’ясувати, чи належить точка 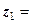 p до круга
p до круга  .
.
Розв’язання. Порівняємо радіус  з відстанню
з відстанню  від центра круга
від центра круга  до точки
до точки 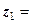 p:
p:
 .
.
Відповідь: точка 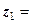 p розміщена поза кругом.
p розміщена поза кругом.
Комплексне число як вектор
Кожному к.ч.  відповідає єдиний радіус-вектор
відповідає єдиний радіус-вектор  , і навпаки, кожному радіусу-вектору
, і навпаки, кожному радіусу-вектору  відповідає єдине к.ч.
відповідає єдине к.ч.  (рис.1.1). Ми будемо зображати к.ч. відповідним йому радіус-вектором
(рис.1.1). Ми будемо зображати к.ч. відповідним йому радіус-вектором  або довільним направленим відрізком, який при паралельному переносі збігається з
або довільним направленим відрізком, який при паралельному переносі збігається з  . Зрозуміло, що модулі к.ч. і відповідного йому вектора рівні.
. Зрозуміло, що модулі к.ч. і відповідного йому вектора рівні.
Якщо вектор  зображає к.ч.
зображає к.ч.  , то домовимось писати
, то домовимось писати  .
.
Нехай  Розглянемо паралелограм
Розглянемо паралелограм  , див. рис.1.3.
, див. рис.1.3.

Рис.1.3
Очевидно, 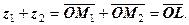
 , тобто сума і різниця к.ч. відповідають сумі і різниці векторів. Таким чином, додавання і віднімання набуває простого геометричного змісту.
, тобто сума і різниця к.ч. відповідають сумі і різниці векторів. Таким чином, додавання і віднімання набуває простого геометричного змісту.
Множення і ділення к.ч.в геометричній формі розглядаються в §1.14.
Приклад. Доведемо нерівність  , яка є узагальненням нерівності абсолютних величин дійсних чисел.
, яка є узагальненням нерівності абсолютних величин дійсних чисел.
Використовуємо простий факт: сума довжин довільних двох сторін трикутника більша довжини третьої сторони. З рис. 1.3 випливає, що  , тобто
, тобто  .
.
Випадок чисел, розміщених на одній прямій пропонуємо розглянути самостійно.
Приклад. Знайти суму і різницю  і
і  , де
, де  ,
,  . Переконатися за допомогою геометричної побудови, що ці вектори можна додавати і віднімати за правилом паралелограма.
. Переконатися за допомогою геометричної побудови, що ці вектори можна додавати і віднімати за правилом паралелограма.
Розв’язання. 
 .
.
Виконати самостійно
В умовах попереднього прикладу знайти  і
і  , де 1)
, де 1)  ,
,  ;
;
2)  ,
,  .
.
4.12. Кут нахилу вектора до осі
Розглянемо довільний ненульовий вектор  (див. рис. 1.4). Величина кута j, утвореного обертанням осі
(див. рис. 1.4). Величина кута j, утвореного обертанням осі  в площині навколо точки
в площині навколо точки  до суміщення її з напрямком вектора
до суміщення її з напрямком вектора  , називається кутом нахилу цього вектора до осі
, називається кутом нахилу цього вектора до осі  ; при цьому j
; при цьому j  , якщо обертання здійснюється проти годинкової стрілки, і j
, якщо обертання здійснюється проти годинкової стрілки, і j  при обертанні за годинковою стрілкою; якщо напрямок
при обертанні за годинковою стрілкою; якщо напрямок  збігається з напрямком
збігається з напрямком  , то j
, то j  .
.

Рис. 1.4
Таким чином, кут нахилу задає напрямок вектора. З рис.1.4. випливає, що додатний j+ і від’ємний j- кути визначають один і той же напрямок.
Очевидно також, якщо довільний кут j задає деякий напрямок, то такий же напрямок будуть задавати і кути  , де
, де  . Отже, за кут нахилу вектора
. Отже, за кут нахилу вектора  можна приймати будь-який з кутів
можна приймати будь-який з кутів  , де
, де  ціле число.
ціле число.
Приклад. Легко перевірити, що кути 1350,4950,-2250,-9450 визначають один і той же напрямок (відносно осі  ).
).






