ѕрактическое зан€тие 3. ќперации с треугольными матрицами
—ведени€ из теории. —ущность метода обращени€ верхней треугольной матрицы разберем на матрицах четвертого пор€дка, а формулы дл€ обращени€ верхней треугольной матрицы любого пор€дка приведем без вывода
ѕусть ј Ц верхн€€ треугольна€ матрица четвертого пор€дка
ј =  .
.
а искома€ обратна€ ей матрица, элементы которой  подлежат определению, запишетс€ в виде
подлежат определению, запишетс€ в виде
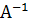 =
=  .
.
ѕо определению обратной матрицы должно выполн€тьс€ равенство

 ·
·  =
=  .
.
»спользу€ правило умножени€ матриц, перемножим матрицы в левой части равенства
 =
=
=  .
.
»сход€ из определени€ равенства двух матриц, дл€ отыскивани€ неизвестных величин получаем уравнени€, сравнив соответствующие элементы первых строк.
 = 1; = 1;
| (1) |
 = 0; = 0;
| (2) |
 = 0; = 0;
| (3) |
 = 0. = 0.
| (4) |
»з этих уравнений следует:
из (1)  ; ;
| (5) |
из (2) 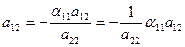 ; ;
| (6) |
из (3) 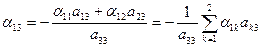
| (7) |
из (4) 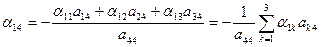
| (8) |
ѕроделав аналогичную работу дл€ второй, третьей и четвертой строк, получим дл€ второй строки
 = 0; = 0;
| (9) |
 = 1; = 1;
| (10) |
 = 0; = 0;
| (11) |
 = 0 = 0
| (12) |
из (9)  = 0. = 0.
| (13) |
— учетом, что  = 0, получаем:
= 0, получаем:
из (10) 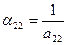 ; ;
| (14) |
из (11)  ; ;
| (15) |
из (12) 
| (16) |
ƒл€ третьей строки
 = 0; = 0;
| (17) |
 = 0; = 0;
| (18) |
 = 1; = 1;
| (19) |
 = 0. = 0.
| (20) |
»з этих уравнений следует:
из (17)  = 0. = 0.
| (21) |
”читыва€, что  = 0, из (18) получаем
= 0, из (18) получаем
 = 0, = 0,
| (22) |
а учитыва€, что и  = 0, и
= 0, и  = 0, находим:
= 0, находим:
из (19)  ; ;
| (23) |
из (20)  ; ;
| (24) |
» наконец, дл€ четвертой строки ищем
 = 0; = 0;
| (25) |
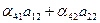 = 0; = 0;
| (26) |
 = 0; = 0;
| (27) |
 = 1. = 1.
| (28) |
»з (25), (26) и (27) следует, что
 = 0; = 0;
| (29) |
 = 0; = 0;
| (30) |
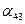 = 0, = 0,
| (31) |
| а с учетом этого и (28) получаем | |
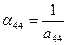 . .
| (32) |
–авенства (9), (21), (22), (29), (30) и (31) показывают, что равны нулю те элементы обратной матрицы 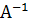 , у которых первый индекс i больше второго индекса j, т.е. если i > j, то
, у которых первый индекс i больше второго индекса j, т.е. если i > j, то
 . .
| (3.1) |
»з равенства (5), (14), (23), (32) диагональные элементы обратной матрицы 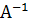 , у которой первый и второй индексы равны (i=j), определ€ютс€ так:
, у которой первый и второй индексы равны (i=j), определ€ютс€ так:
 ;
; 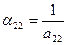 ;
;  ;
; 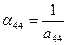 ,
,
что можно объединить одной записью: если i = j, то
 . .
| (3.2) |
ѕо формулам (6), (7), (8), (15), (16), (24) и (32) определ€ютс€ те элементы обратной матрицы дл€ верхней треугольной, у которых первый индекс i меньше второго индекса j (i<j), т.е. элементы, сто€щие над главной диагональю. ѕолученна€ по этим формулам обратна€ матрица будет также верхней треугольной.
огда верхн€€ треугольна€ матрица имеет пор€док n, элементы обратной ей матрицы наход€тс€ по аналогичным формулам, которые имеют следующий вид:
если i = j, то  ; ;
| (3.3) |
если i > j, то  ; ;
| (3.4) |
если i < j, то  ; ;
| (3.5) |
Ќапример, по формуле (3.5) элемент обратной матрицы п€того пор€дка
 . .
| (3.6) |
«амечани€. ѕримен€€ формулу (3.5), надо иметь в виду, что будут равны нулю те произведени€, в которых первый индекс элемента α больше второго индекса. ћожно указать простое правило дл€ определени€ элементов обращенной верхней треугольной матрицы.
|
|
|
1. ќпределить диагональные элементы обращенной матрицы по формуле (3.3)
2. ѕосле этого подписать матрицы одну под другой.
3. Ќа места элементов, сто€щих ниже главной, вписать нули.
4. „тобы определить элемент, сто€щий над главной диагональю обратной матрицы, надо составить алгебраическую сумму произведений элементов, сто€щих в обратной матрице 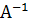 , левее определ€емого, на соответствующие элементы того столбца матрицы ј (т.е. той матрицы, дл€ которой ищетс€ обратна€), в котором стоит определ€емый элемент. Ёту алгебраическую сумму надо разделить на диагональный элемент матрицы ј, сто€щий в том же столбце, что и определ€емый элемент. ќпредел€емый элемент равен этому частному, вз€тому с обратным знаком.
, левее определ€емого, на соответствующие элементы того столбца матрицы ј (т.е. той матрицы, дл€ которой ищетс€ обратна€), в котором стоит определ€емый элемент. Ёту алгебраическую сумму надо разделить на диагональный элемент матрицы ј, сто€щий в том же столбце, что и определ€емый элемент. ќпредел€емый элемент равен этому частному, вз€тому с обратным знаком.
ѕо этому правилу выражение в скобках в (3.6) получаетс€ так: искомый элемент  матрицы
матрицы 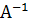 находитс€ в первой строке и п€том столбце. ѕеред ним в первой строке обратной матрицы
находитс€ в первой строке и п€том столбце. ѕеред ним в первой строке обратной матрицы 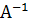 сто€т элементы
сто€т элементы 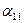 ,
,  ,
,  и
и  , а в п€том столбце матрицы ј Ц элементы
, а в п€том столбце матрицы ј Ц элементы  ,
,  ,
,  и
и  . —оставл€етс€ алгебраическа€ сумма произведений первого элемента в первой строке матрицы
. —оставл€етс€ алгебраическа€ сумма произведений первого элемента в первой строке матрицы 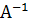 на второй элемент в п€том столбце матрицы ј и т.д. ƒл€ у€снени€ этого правила решим несколько задач.
на второй элемент в п€том столбце матрицы ј и т.д. ƒл€ у€снени€ этого правила решим несколько задач.
«адача 3.1 Ќайти обратную матрицу дл€ матрицы
ј =  .
.
–ешение. п. 1.Ќаходим диагональные элементы 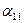 ,
,  ,
,  и
и  обращенной матрицы по формуле (3.3)
обращенной матрицы по формуле (3.3)
 ;
;  ;
;  ;
;  .
.
пп. 2 и 3. ѕодписываем матрицы одну под другой и вписываем нули на места элементов, сто€щих под главной диагональю
ј = 
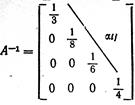
п. 4. ќпредел€ем элементы  , сто€щие над главной диагональю (i < j), по формуле (3.5), пользу€сь указанным в п.4 правилом.
, сто€щие над главной диагональю (i < j), по формуле (3.5), пользу€сь указанным в п.4 правилом.
 ;
;
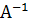 =
= 
ƒл€ проверки надо перемножить матрицы ј и 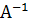 и убедитс€, что получитс€ единична€ матрица
и убедитс€, что получитс€ единична€ матрица
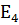 =
=  .
.
ѕри решении этой задачи все элементы обратной матрицы были представлены в виде простых дробей дл€ облегчени€ контрол€. Ќа практике же все вычислени€ ведутс€ в дес€тичных дроб€х.






