По окончанию изучения тем учебной дисциплины студентам необходимо выполнить контрольную работу.
Образец титульного листа представлен в ПРИЛОЖЕНИИ 1.
Темы контрольных работ представлены в ПРИЛОЖЕНИИ 2.
Требования к структуре, написанию и оформлению контрольной работы или реферату изложены в «Методических рекомендациях по написанию и оформлению письменных работ» ОТДИС/ЗО – 2012г.
Промежуточная форма аттестации - дифференцированный зачет (с оценкой), который осуществляется по результатам защиты темы контрольной работы.
ПРИМЕЧАНИЕ:
1) Решения должны сопровождаться краткими, но вразумительными объяснениями, в необходимых случаях должны быть ссылки на учебник. Например, “составляем уравнение прямой, проходящей через две точки…”, ”в силу геометрического смысла векторного произведения…”, “По определению непрерывности функции в точке…” и т.п.
2) Объяснения должны относиться строго к тексту задачи и, соответственно, к теме курса.
3) Формулы сокращенного умножения, решение квадратных уравнений объяснять не нужно.
4) При работе над ошибками – читать замечания и указания проверяющего и, по возможности, выполнять их в работе, присылаемой на повторную проверку – вместе с предыдущей работой!
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО контрольной работе
Вариант контрольной работы выбирается студентом в соответствии с 2-мя последними цифрами зачётной книжки. Задания - по таблице 2.
ОПРЕДЕЛЕНИЕ ВАРИАНТА ЗАДАНИЯ
Таблица 1
| Последние цифры шифра зачетной книжки студента | № варианта | Последние цифры шифра зачетной книжки студента | № варианта |
| 01, 21, 41, 61, 81 | 11, 31, 51, 71, 91 | ||
| 02, 22, 42, 62, 82 | 12, 32, 52, 72, 92 | ||
| 03, 23, 43, 63, 83 | 13, 33, 53, 73, 93 | ||
| 04, 24, 44, 64, 84 | 14, 34, 54, 74, 94 | ||
| 05, 25, 45, 65, 85 | 15, 35, 55, 75, 95 | ||
| 06, 26, 46, 66, 86 | 16, 36, 56, 76, 96 | ||
| 07, 27, 47, 67, 87 | 17, 37, 57, 77, 97 | ||
| 08, 28, 48, 68, 88 | 18, 38, 58, 78, 98 | ||
| 09, 29, 49, 69, 89 | 19, 39, 59, 79, 99 | ||
| 10, 30, 50, 70, 90 | 20, 40, 60, 80, 00 |
Таблица распределения заданий по вариантам
Таблица 2
| Варианты | № задания |
| 1.1; 2.1; 3.1; 4.1; 5.1; 6.1; 7.1; 8.1; | |
| 1.2; 2.2; 3.2; 4.2; 5.2; 6.2; 7.2; 8.2; | |
| 1.3; 2.3; 3.3; 4.3; 5.3; 6.3; 7.3; 8.3; | |
| 1.4;2.4; 3.4;4.4; 5.4;6.4; 7.4; 8.4; | |
| 1.5;2.5; 3.5;4.5; 5.5;6.5; 7.5; 8.5; | |
| 1.6;2.6; 3.6;4.6; 5.6;6.6; 7.6; 8.6; | |
| 1.7;2.7; 3.7;4.7; 5.7;6.7; 7.7; 8.7; | |
| 1.8;2.8; 3.8;4.8; 5.8;6.8; 7.8; 8.8; | |
| 1.9;2.9; 3.9;4.9; 5.9;6.9; 7.9; 8.9; | |
| 1.10;2.10; 3.10;4.10; 5.10;6.10; 7.10;8.10; | |
| 1.6;2.1; 3.6;4.1; 5.2;6.4; 7.2; 8.4; | |
| 1.7;2.3; 3.7;4.3; 5.1;6.2; 7.1; 8.2; | |
| 1.8;2.5; 3.8;4.5; 5.4;6.8; 7.4; 8.8; | |
| 1.9;2.7; 3.9;4.7; 5.5;6.10; 7.5; 8.10; | |
| 1.10;2.9; 3.10;4.9; 5.3;6.6: 7.3;8.6: | |
| 1.1;2.2; 3.1;4.2; 5.8;6.5; 7.8;8.5; | |
| 1.2;2.4; 3.2;4.4; 5.10;6.9; 7.10;8.9; | |
| 1.3;2.6: 3.3;4.6: 5.7;6.3; 7.7;8.3; | |
| 1.4;2.8; 3.4;4.8; 5.9;6.7; 7.9;8.7; | |
| 1.5;2.10; 3.5;4.10; 5.6;6.1; 7.6;8.1; |
ЗАДАНИЯ КОНТРОЛЬНОЙ РАБОТЫ № 1
Линейная алгебра
Задание № 1
Вычислить определитель.
1.1.  . 1.2.
. 1.2.  . 1.3.
. 1.3.  . 1.4.
. 1.4.  .
.
1.5.  . 1.6.
. 1.6.  . 1.7.
. 1.7.  . 1.8.
. 1.8.  . 1.9.
. 1.9.  . 1.10.
. 1.10.  .
.
Задание № 2
Решить систему уравнений по правилу матричным методом.
2.1.  2.2.
2.2. 
2.3.  2.4.
2.4. 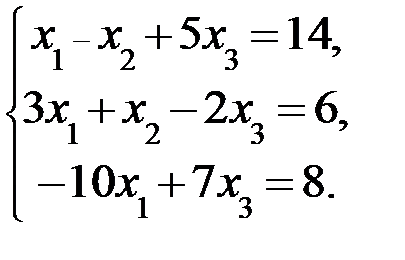
2.5.  2.6.
2.6. 
2.7.  2.8.
2.8. 
2.9.  2.10.
2.10. 
Задание № 3
Решить систему уравнений методом Гаусса.
3.1.  . 3.2.
. 3.2.  . 3.3.
. 3.3.  .
.
3.4.  . 3.5.
. 3.5.  . 3.6.
. 3.6.  .
.
3.7.  . 3.8.
. 3.8.  . 3.9.
. 3.9.  .
.
3.10.  .
.
Векторная алгебра. Задание № 4
Найти площадь и длины диагоналей параллелограмма, построенного на векторах  .
.
4.1.  .
.
4.2.  .
.
4.3.  .
.
4.4.  .
.
4.5.  .
.
4.6.  .
.
4.7.  .
.
4.8.  .
.
4.9.  .
.
4.10.  .
.
Задание № 5
5.1. Найти уравнение плоскости, проходящей через точки  .
.
5.2. Найти уравнение плоскости, проходящей через точки  и параллельной оси ОХ.
и параллельной оси ОХ.
5.3. Найти уравнение плоскости, проходящей через точки  и параллельной оси ОУ.
и параллельной оси ОУ.
5.4. Найти уравнение плоскости, проходящей через точки  и параллельной оси ОZ.
и параллельной оси ОZ.
5.5. Найти уравнение плоскости, проходящей через точку  и ось ОХ.
и ось ОХ.
5.6. Найти уравнение плоскости, проходящей через точку  и ось ОУ.
и ось ОУ.
5.7. Найти уравнение плоскости, проходящей через точку  и ось ОZ.
и ось ОZ.
5.8. Найти уравнение плоскости, проходящей через точку  и перпендикулярной плоскостям
и перпендикулярной плоскостям 
5.9. Найти уравнение плоскости, проходящей через точку  и параллельной векторам
и параллельной векторам  .
.
5.10. Найти уравнение плоскости, проходящей через начало координат и точки  .
.
Задание № 6
Установить, что каждое из следующих уравнений определяет гиперболу, и найти координаты ее центра С, полуоси, эксцентриситет, уравнения асимптот и уравнения директрис. Изобразить гиперболу на чертеже, указав фокусы, асимптоты и директрисы.
6.1. 
6.2. 
6.3. 
6.4. 
6.5. 
Установить, что каждое из следующих уравнений определяет эллипс, и найти координаты его центра С, полуоси, эксцентриситет, уравнения директрис. Изобразить эллипс на чертеже, указав оси симметрии, фокусы и директрисы.
6.6. 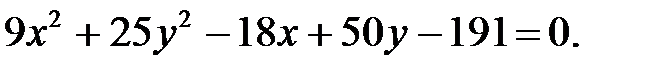
6.7. 
6.8. 
6.9. 
6.10. 
Задание № 7
Найти интеграл.
7.1.  . 7.2.
. 7.2.  . 7.3.
. 7.3.  .
.
7.4.  . 7.5.
. 7.5.  . 7.6.
. 7.6.  .
.
7.7.  . 7.8.
. 7.8.  . 7. 9.
. 7. 9.  .
.
7.10.  .
.
Задание № 8
Найти интеграл.
8.1.  . 8.2.
. 8.2.  . 8.3.
. 8.3.  8.4.
8.4. 
8.5..  . 8.6.
. 8.6.  . 8.7.
. 8.7.  ..
..
8.8.  . 8.9.
. 8.9.  . 8.10.
. 8.10.  .
.




