Функцияның нүктелік квадраттық аппроксимациясы

Лекция № 1-6. Функцияға жуықтау.

Кіші квадраттар әдісі.

Сплайндар арқылы жуықтау.

Кiшi квадраттар әдiсi

 

интервалында берілген -функцияға жуықтау деп, -функцияны оған жақын болған басқа функциямен алмастыруды айтамыз. Функцияны жуықтауға алып келетін есеп келесідей қарапайым жолмен құрылады:

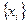торында функция кесте түрінде берілсін

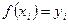, i=0,1, …,n.

Бастапқы 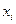торының түйіндерімен сәйкес келмейтіндей 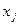нүктесіндегі функциясының мәнін табу керек.

Мысал қарастырып көрейік. ЭЕМ-де күрделі функциясының мәнін әртүрлі көп нүктеде есептеу керек болсын. Оны тікелей есептеудің орнына -тың мәндерін арнайы нүктелерде есептеп, ал қалған 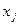нүктелерде осы белгілі мәндер туралы мәліметтерді пайдалана отырып функцияның мәндерін қандайда бір қарапайым формула арқылы есептеуге де болады.

Бұл қарапайым формула -ты, осы 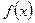-қа қарағанда қарапайым түрге ие болатын 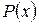функциясымен ауыстырып алудан келіп шығуы мүмкін.

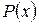функциясын жуықтауды көбінесе мына түрде қояды:

,

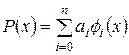мұндағы 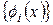- 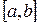кесіндісінде анықталған және тегіс болып табылатын (үздіксіз дифференциалданатын) функциялар жүйесі; - жиында 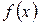-тың 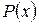-қа ең аз ауытқуындағы мәндерінің коэффициенттері.

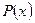полиномы аппроксимациялаушы немесе жуықтаушы деп аталады.

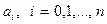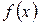Егер параметрлері торабында , яғни пен 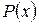-тың сәйкес мәндер шартымен анықталса, онда мұндай жуықтау әдісін интерполяция немесе интерполяцияланушы деп атаймыз, ал 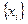кестесін интерполяциялық кесте деп атайды. Бұған қоса, 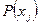-ды есептеу қажет болып отырған 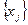кесте мәні (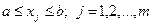) тордың шекарасынан аспайды. Егер біз 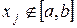нүктесіндегі 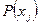мәнін есептейтін болсақ, онда жуықтауды экстраполяция деп атайды.

Егер 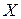жиыны 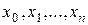нүктелерден құралса, онда жуықтау нүктелік деп аталады. Егер 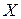жиыны аралықтан тұрса, онда жуықтауды интерполяция деп атайды.

 

 

Функцияның нүктелік квадраттық аппроксимациясы

 

Біз жоғарыда дәрежесі интерполяция түйіндерінің санымен сәйкес келетін аппроксимациялаушы полиномды құрдық. Егер түйіндер саны 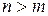болса, (мұнда 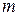- полином дәрежесі), ондай жағдай нүктелік квадраттық аппроксимацияға алып келеді.

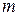-ші дәрежелі полиномды қарастырамыз

 

.

 

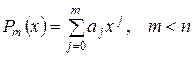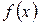функциясының 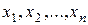нүктелер жиынында аппроксимациялық полиномынан ауытқу өлшемі ретінде квадраттық ауытқу деп аталатын

 

,

- шаманы қабылдайды.

 

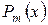интерполяциялық полиномын құру үшін 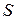минимальды болатындай 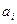коэффициенттерін алу қажет. 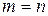болғанда коэффициенттер жүйеден табылады,

 

,

 

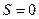сонда Лагранж полиномы үшін алда келтірілген формуласын аламыз.

Есепті шешу үшін көп айнымалы функцияның минимум болуының қажетті шартын пайдаланамыз

 

,

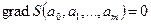Немесе

 

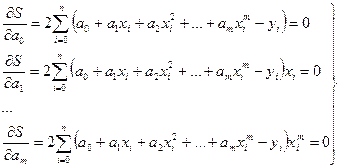. (6.6.1)

 

 

Белгілеулер енгіземіз

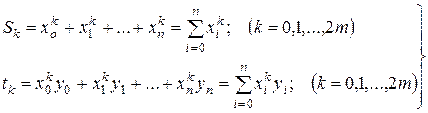. (6.6.2)

 

(6.6.1) жүйесін (6.6.2)-ге қатысты түрлендіреміз

 

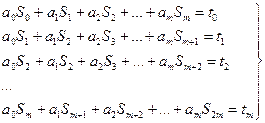, (6.6.3)

 

Мұнда .

Егер 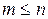және бір-бірімен сәйкес келмесе, онда (6.8.3) жүйесінің анықтаушы нөлден айрықша және жүйенің бір шешімі болады.

 

.

 

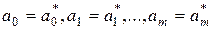Осындай коэффициенттермен алынған полином минимальды квадраттық ауытқуға ие.

Егер 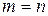болса, онда 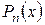аппроксимацияланған полином Лагранж полиномымен және 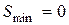сәйкес келеді.

Әсіресе, тәжірибеде дәрежелі полином 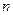-нен кіші болады, сондықтан бізге (6.6.3) формуласы бойынша жуықтау полиномын құруға тура келеді.