З урахуванням наведених вище співвідношень комплексне число можна представити у вигляді
.
Така форма запису комплексного числа називається тригонометричною, а множення, ділення та піднесення до натурального степеня виконуються за формулами
;
;
.
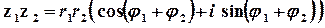З урахуванням формули Ейлера 
комплексне число може бути записано у показниковій формі
.
Якщо комплексні числа записані у показниковій формі, то дії множення, ділення та піднесення до натурального степеня виконуються за правилами
;
;
.
Коренем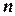 
-го степеня з комплексного числа 
називається таке число, 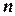-ий степінь якого дорівнює . Обчислення кореня виконується за формулою
, 
,
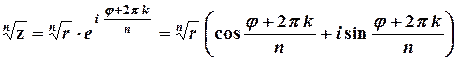тобто корінь 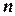-го степеня має 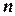значень.
ПИТАННЯ ТА ЗАВДАННЯ ДЛЯ
САМОСТІЙНО
ОПРАЦЮВАНОГО МАТЕРІАЛУ
Тема 1. Дії над комплексними числами.
Завдання для самоконтролю:
1.1 Виконати арифметичні дії з комплексними числами 
і 
1.2 Подати вираз у вигляді двох спряжених комплексних чисел: 1) 
;
2) 
; 3) 26.
1.3 Обчислити степені: 
; 
; 
; 
.
Питання для самоконтролю:
1. Чи можуть сума, різниця, добуток к і частка двох комплексних чисел дорівнювати дійсному числу?
2. Чому дорівнюють сума та добуток двох спряжених комплексних чисел?
3. Скільки різних степенів має уявна одиниця?
Тема 2. Геометрична інтерпретація комплексних чисел.
Завдання для самоконтролю:
2.1. Знайти геометричне зображення комплексних чисел: 
.
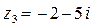2.2. Виконати додавання і віднімання комплексних чисел у геометричній формі:
а)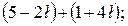 
б) 
Питання для самоконтролю:
1. В яких чвертях розміщені точки, що зображають комплексні числа: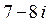 
; 
;
; 
.
2. Що можна сказати про взаємне розміщення точок, які зображують спряжені комплексні числа? протилежні комплексні числа?
3. Як можна геометрично інтерпретувати додавання і віднімання двох комплексних чисел?
Тема 3. Показникова форма запису комплексних чисел.
Завдання для самоконтролю:
3.1. Записати комплексне число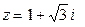 
в тригонометричній та показникові формах.
3.2. Знайти 
та 
, якщо 
.
Питання для самоконтролю:
1. Формули переходу від алгебраїчної форми запису комплексного числа z показникової форми.
2. Дії з комплексними числами, що задані в показникові формі (алгебраїчна сума,
множення, ділення, піднесення до степеня і добування кореня).
ЛІТЕРАТУРА:
1. Шкіль М. І., Колесник Т. В., Котлова В.М. Вища математика. – К.:Вища школа,1984.
2. Баврин И. И. Высшая математика. – М.: Просвещение. 1986.
3. Кривуца В.Г., Барковський В.В., Барковська Н.В. Вища математика. Практикум:
Навчальний посібник. – К.: Центр навчальної літератури, 2005.
ВІДПОВІДІ ДО ЗАВДАНЬ САМОКОНТРОЛЮ:
1.1 
; 
; 
; 
.
1.2 1) 
; 2) 
; 3) 
.
1.3 
; 
; 
; 
.
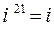2.1 2.2 а)
2.2 б)
3.1. 
3.2. 
; 
.
