Если бы расстояние между электродами точно равнялось 1 см, а площадь каждого электрода - 1 см2 и в прохождении тока участвовал только один объем раствора, заключенный между электродами, то электропроводность, измеренная в таких условиях, представляла бы собой удельную электропроводность раствора. Практически
Причем все ионы остаются между электродами, участвуя в переносе электричества. Следовательно, возрастание эквивалентной электропроводности раствора данного электролита при разбавлении определяется степенью электролитической диссоциации и вместе с ней, по мере разбавления, стремится к пределу, после которого остается постоянной. Это предельное значение электропроводности называется электропроводностью при бесконечном разведении и обозначается 
. Электропроводность при бесконечном разведении вычисляется как сумма подвижностей ионов (катионов - 
и анионов - 
): 
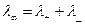
Определив эквивалентную электропроводность раствора и, зная подвижность ионов, можно вычислить степень диссоциации по формуле:
.
Степень диссоциации слабого электролита в водном растворе с разбавлением V определяется частным от деления значения эквивалентной электропроводности при этом разбавлении на значение электропроводности при бесконечном разведении.
В растворах слабых электролитов имеются недиссоциированные молекулы, а также катионы и анионы, образовавшиеся вследствие электролитической диссоциации некоторой части молекул. Между ними в растворе устанавливается динамическое (подвижное равновесие, характеризуемое при данной температуре и данной общей концентрации электролита постоянной величиной – константой электролитической диссоциации, которую можно вычислить на основании закона действующих масс. Для молекул, способных диссоциировать на два иона, КА Û К+ + А-:
, где /4/
К – константа электролитической диссоциации;
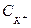- концентрация катионов;
- концентрация анионов;
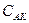- концентрация недиссоциированных молекул.
Если концентрацию электролита в объеме V принять равной С:
= 
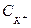= a . С, тогда концентрация недиссоциированных молекул определяется по формуле:
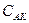= (1 - a) . С, учитывая это, получим для константы диссоциации:
. /5/
Учитывая, что V = 1/С, получим:
. /6/
Подставим значение степени диссоциации в /6/:
= 
/7/
Последние два уравнения носят название закона разведения Оствальда. Целью данной работы является проверка настоящего закона.
Экспериментальная часть
Методика измерений
Так как электропроводность – это величина, обратная сопротивлению, то, практически, определение электропроводности сводится к определению сопротивления. Наиболее пригодным в этом случае является метод, основанный на применении переменного тока по схеме мостика Уитстона. Допустим, ток идет из источника Е к точке А (рис.1), где он разветвляется и часть тока идет через D к С, а другая – через В к С. От точки С ток идет обратно к источнику тока.
Рис.1
Сопротивления частей цепи будут:
АВ = R1, BC = R2, AD = R3, DC = R4.
Если точки D и В соединить проводником, то по нему может пойти ток. По закону Кирхгофа, в проводнике ВD тока не будет в том случае, когда будет соблюдаться следующее соотношение:
.
Зная три из этих сопротивлений, можно вычислить четвертое. На опыте в качестве R2 берется определенное сопротивление магазина; R1 – сосуд с электролитом, электропроводность которого нужно определить; R3 и R4 – берется реохорд, плечи которого будут соответственно a и b. Для измерения сопротивления жидкостей применяют переменный ток, а не постоянный, чтобы избежать электролиза и поляризации.
Очень чувствительным прибором, обнаруживающим присутствие или отсутствие тока в мостике, является низкоомный телефон, вибрационный гальванометр или осциллограф. В качестве источника переменного тока применяется звуковой генератор ЗГ-1. Схема присоединения приборов для измерения сопротивления жидкостей изображена на рис. 2.
Лабораторная работа № 16
