Одним з головних розділів математичного програмування є лінійне програмування. Це область математики, що вивчає задачі відшукання екстремуму (максимум, мінімум) лінійної функції на області допустимих значень змінних, окресленої обмеженнями у вигляді лінійних рівнянь та нерівностей, які пов’язують ці змінні.
До задач лінійного програмування зводиться широке коло задач управління функціонуванням економічних систем.
Задачі лінійного програмування тісно пов’язані з задачами теорії ігор, тому щодо їхнього розв’язування можна застосовувати числові методи теорії ігор.
Важливими для економічного аналізу є положення теорії двоїстості у лінійному програмуванні, яка вивчає загальні властивості пари тісно пов’язаних між собою двоїстих задач лінійного програмування. Пара двоїстих задач лінійного програмування в інтерпретації найпоширенішої задачі виробничого планування виглядає так.
Головним досягненням математичного аналізу задач лінійного програмування є формулювання загальної ознаки оптимальності допустимого розв’язку задачі без необхідності порівняння цього розв’язку з усіма іншими допустимими розв’язками цієї задачі.
Лінійне програмування знаходить своє застосування у різних сучасних і класичних областях математики: теорії графів, комбінаториці, теорії наближення функцій, теорії лінійних нерівностей та інших.
Важливим розділом математичного програмування є нелінійнепрограмування. Цей розділ математичного програмування вивчає методи відшукання розв’язків багатовимірних екстремальних задач з обмеженнями, причому функціональні залежності у цих задачах не вважають лінійними. Суть загальної задачі нелінійного програмування полягає у визначенні n -вимірного вектора x=(x 1, x 2, …, x n ) з заданими функціями f (x), g 1 (x), g 2 (x), …, g m (x), який надавав би функції f(x) глобального екстремуму і задовольняв би умови:
g i(x)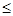 
0, i= 1, 2, …, m; xj 
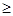0, j= 1, 2, …, n,
які означають множину M допустимих значень вектора X.
Нелінійне програмування охоплює дуже широке коло задач математичного програмування. Важливим для пошуку розв’язання задачі нелінійного програмування є метод множників Лагранжа, який передбачає побудову функції Лагранжа:
F(x,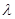 
)=f(x) + 
,
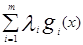де число 
– множники Лагранжа.
Блокове програмування
Блокове програмування – розділ лінійного програмування, який вивчає методи зведення розв’язування задач лінійного програмування великого обсягу до розв’язування послідовності задач меншої розмірності. Основу блокового програмування становить метод декомпозиції.
Дискретне програмування
