Признаки подобия треугольников
Тема: «Признаки подобия треугольников».
- признаки равенства треугольников?
- какие треугольники называются подобными?
- первый признак подобия треугольников?
І Признак подобия.
Если два угла одного треугольника равны соответствующим двум углам другого треугольника, то такие треугольники подобны между собой.
  
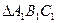
| ІІ Признак подобия.
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы между ними равны, то эти треугольники подобны.
Если  
 
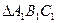
| ІІІ Признак подобия.
Если три стороны одного треугольника пропорциональны соответствующим трем сторонам другого треугольника, то эти треугольники подобны.
Если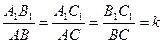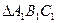 
|
Следствие 1
Если острый угол одного прямоугольного треугольник равен острому углу другого прямоугольного треугольника, то эти прямоугольные треугольники подобны.
 и  - прямоугольные.
Если 
| Следствие 2
Если два катета прямоугольного треугольника пропорциональны соответствующим двум катетам другого прямоугольного треугольника, то эти прямоугольные треугольники подобны
и - прямоугольные.
Если 
| Следствие 3
Если гипотенуза и катет одного прямоугольного треугольника пропорциональны гипотенузе и соответствующему катету другого прямоугольного треугольника, то эти прямоугольные треугольники подобны
и - прямоугольные.
Если 
|
Задача 1 (устно)
Будут ли подобны друг другу равносторонние треугольники?
Задача. Дано два треугольника две стороны, которого пропорциональны, а углы между этих сторон равны. Доказать что треугольники подобны.
. 
Рис. 2
Доказательство. Изобразим вспомогательный Рис. 3. На нем отложим в первом треугольнике 
, через точку 
проведем отрезок 
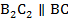до пересечения с продолжением стороны 
в точке 
.
Рис. 3
Рассмотрим треугольники 
и 
. 
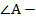общий, 
как соответственные при параллельных прямых, пересеченных секущей, следовательно, 
по первому признаку подобия.
По определению подобных треугольников, 
, а по условию 
, следовательно, 
, т.к. по построению. В результате
имеем: 
по первому признаку равенства треугольников. А т.к. доказано, что , то и 
, что и требовалось доказать.
Из данной задачи следует Второй признак подобия треугольников (по двум сторонам и углу между ними). Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы между этими сторонами равны, то такие треугольники подобны (см. Рис. 2).
Задача 2. В заданном треугольнике проведены все средние линии. Среди образованных таким образом треугольников покажите подобные.
Дано:
- средние лини.
Определить подобные 
-ки?
Решение:
подобен
подобен По 2 признаку
подобен
подобен по 3 признаку подобия.
А по 3 свойству преобразования подобия следует:
, , , , -подобны.
Теорема (3-й признак подобия треугольников). Если три стороны одного треугольника соответственно пропорциональны трём сторонам другого треугольника, то такие треугольники подобны.
Доказательство.
Делаем дополнительные построения:
Отложим от точки А угол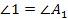 
, а из вершины С 
,. Они пересекутся в точке В2 . Тогда 
по первому признаку. Тогда из подобия треугольников следует пропорциональность сторон: 
, а по условию получаем что АВ=АВ2, ВС=В2С.
Тогда 
по 3 признаку.
Следовательно 
Так как 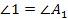, то 
Следовательно 
. Что и требовалось доказать.
Задача 3. Будут ли два треугольника подобны, если их стороны равны: 1 м, 1,5 м, 2 м и 10 см, 15 см, 20 см?
Дано:
и
;
;
;
-?
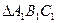
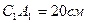
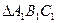Решение: Найдем отношение 
, 
, 
=>
подобен 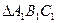по 3 признаку подобия треугольников, с коэффициентом подобия равным 
.
Задача 4. Будут ли треугольники и 
подобны, если в этих треугольниках: 
и 
Дано:
и 
;
;
;
-?
Решение: Найдем отношение соответствующих сторон треугольников: 
; 
, т.е стороны треугольников не являются пропорциональными, значит треугольники не подобны.
Задача 5. Дерево высотой 15 м закрывается монетой диаметром 2 см, если ее держать на расстоянии 70 см от глаз. Найдите расстояние от наблюдателя до дерева.
Д/з. Задача 1Будут ли два треугольника подобны, если их стороны равны: 1) 1,2 м, 1,6 м, 2,4 м и 3 см, 4 см, 6 см.
Задача 2. Будут ли два треугольника подобны, если их стороны равны: 1) 0,4 см, 0,6 см, 1 м и 8 см, 12 см, 20 см.
Задача 3. Будут ли треугольники и подобны, если в этих треугольниках: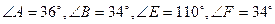 
?
Задача
Дано:
и
;
;
;
-?
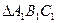
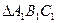Решение: Найдем отношение соответствующих сторон треугольников 
, 
, 
=>
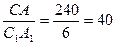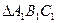подобен по 3 признаку подобия треугольников, с коэффициентом подобия равным 
.
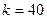№432 (2).
Дано:
и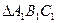
;
;
;
-?
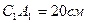
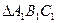Решение: Найдем отношение соответствующих сторон треугольников 
, 
, 
=> 
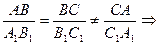
не является подобным .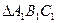
№ 435 (1).
Дано:
и 
-?
Решение: Вычислим величину угла 
треугольника : 
, значит 
и 
данные треугольники подобны по второму признаку.
