Проверка правильности алгоритма.

Постановка задачи

Прежде, чем понять задачу её, необходимо четко сформулировать. Обычно процесс точной формулировки задачи сводится к постановке правильных вопросов.

1. Понятна ли терминология?

2. Что дано?

3. Что нужно найти?

4. Как определить решение?

5. Каких данных не хватает и все ли они нужны?

6. Являются ли какие-то данные бесполезными?

7. Какие сделаны допущения?

Сформулируем постановку на примере.

"Задача Коммивояжера".

Агент по продаже компьютеров должен посетить 20 городов. Компания возмещает ему 50% стоимости дорожных расходов. Известна цена проезда между каждыми двумя городами. Коммивояжеру хотелось бы снизить дорожные расходы.

Что дано? Исходная информация в виде перечня городов. Известно:

· Количество городов

· Стоимость переезда из города i в город j

Комментарий: в принципе, можно сразу отметить, что дана матрица стоимостей С: с_ij- стоимость переезда из i в j.

Что хотим найти? Как снизить дорожные расходы. То есть, найти такую последовательность объезда городов, что стоимость всего пути будет наименьшей.

Необходима ли дополнительная информация? Есть ли приоритеты в городах?

Дополнительная информация: Маршрут начинается и кончается в базовом городе и проходит по одному разу через все остальные города.

Что надо получить? Список городов, содержащий каждый город только один раз, за исключением базового города, который стоит в списке первым и последним.

Сумма стоимостей между каждыми двумя городами маршрута - это общая стоимость маршрута представленного списка. Необходимо представить список наименьшей стоимости.

Построение модели

Задача четко сформулирована, теперь необходимо составить для неё математическую модель. Выбор модели существенно влияет на остальные этапы решения задачи. Невозможно предложить набор правил, автоматизирующих этап моделирования. Приступая к разработке модели, следует, по крайней мере, задать два основных вопроса:

· Какие математические структуры больше всего подходят для задачи (это может сразу упростить ее и повлиять на выбор алгоритма)

· Существует ли решенные аналогичные задачи. (На что похоже, в чем отличие)

Второй вопрос, возможно, самый полезный во всей математике.

В контексте моделирования он часто дает ответ на первый вопрос. Действительно, большинство решаемых в математике задач, как правило, являются модификациями ранее решенных. Большинство из нас просто не обладает талантом Ньютона, Гаусса или Эйнштейна, и для продвижения вперед нам приходится руководствоваться накопленным опытом.

Итак, отвечая на первый вопрос, мы должны описать на языке математики, что нам дано и что хотим найти, сделать выбор математических структур, а затем задачу необходимо сформулировать в терминах соответствующих математических объектов.

Это будет одна из возможных моделей, если мы можем утвердительно ответить на следующие вопросы:

1. Вся ли важная информация задачи описана математическими объектами?

2. Существует ли математическая величина, ассоциируемая с искомым результатом?

3. Выявлено ли какое-нибудь полезное соотношение между объектами модели?

4. Можно работать с моделью? Удобно ли с ней работать?

"Задача Коммивояжера".

Решали ли мы раньше подобные задачи? Вероятно, нет, однако мы сталкивались с задачей выбора пути по дорожным картам или в лабиринте. Представим нашу задачу наподобие карты. Города - это точки, соединенные отрезками, на которых проставлена стоимость проезда из первого города во второй. (Длины отрезков при этом роли не играют).

Очевидно, нужно взять лист бумаги и нанести на нем по одной точке, соответствующей каждому городу. Мы не собираемся изображать точки так, чтобы расстояние между каждой парой точек, соответствующих городам i и j, было пропорционально стоимости проезда с_ij Расположим точки любым удобным способом, соединим точки i и j линиями и проставим на них «веса» с_ij

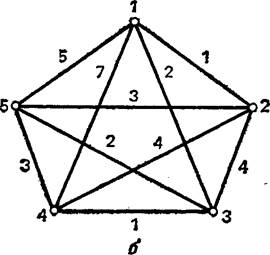
рис.1

Схема, которую мы только что изобразили,— это частный случай известного в математике графа, или сети. В общем случае сеть — это множество точек (на плоскости) вместе с линиями, соединяющими некоторые или все пары точек; над линиями могут быть проставлены веса., что мы и сделали.

Каждый граф можно представить на плоскости множеством точек, соответствующих вершинам, которые соединены линиями, соответствующими ребрам. Вершины графа на рисунке выделяют обычно кружочками или квадратиками, так как не всегда точки пересечения ребер являются вершинами графа.

Т.е., можно сказать, что граф - это конечное множество вершин V и набор E - пар вершин. Обозначение G=(V,E).

Известны различные способы представления графов в памяти компьютера, которые различаются объемом занимаемой памяти и скоростью выполнения операций над графами.

Для нашей задачи рассмотрим представление графа в виде матрицы стоимостей. Предположим, что стоимость проезда из города i в город j такая же как и из города j в город i, хотя, вообще говоря, это не всегда так. Как видно из примера на рис.1, в нашем случае число городов равно 5. Заполним матрицу стоимостей С

-

-

-

-

-

Что ищем? В терминах теории графов список городов определяет замкнутый цикл, начинающийся с базового города и возращающийся туда же после прохождения каждой вершины графа по одному разу. Такой цикл называется гамильтоновым циклом. Задача решена, если мы нашли гамильтонов цикл с наименьшей стоимостью.

Например, для графа на рис.1 гамильтонов цикл 1 – 5 – 3 – 4 – 2 – 1 имеет стоимость:

5+2+1+4+1=13

Является ли он маршрутом с минимальной стоимостью? Это пока неизвестно.

Рассмотренная задача, известная в литературе как задача коммивояжера, стала в какой-то мере классической. Это один из наиболее известных примеров таких задач, которые очень легко поставить и промоделировать, но очень трудно решить. Время от времени мы будем возвращаться к этой задаче в целях иллюстрации разных подходов к ее решению, оценки сложности алгоритма и т.п.

Разработка алгоритма.

Выбор алгоритма зависит от выбранной модели. Два разных алгоритма могут быть правильными, но сильно отличаться по эффективности работы. Критерии эффективности различных алгоритмов и способы оценки мы рассмотрим позже, а сейчас попытаемся описать самый очевидный подход к алгоритму решения нашей задачи.

«Исчерпывающий алгоритм» решения задачи коммивояжера

Произвольно пронумеруем города целыми числами от 1 до n. Базовому городу припишем номер n. Таким образом, каждый гамильтонов цикл однозначно соответствует перестановке целых чисел:

n 1, 2, 3, … n-1, n

n n-5, 2, 3, …, n-1, n-2 n и др.

Для любой перестановки мы можем проследить гамильтонов цикл на графе, и в то же время вычислить стоимость соответствующего пути.

Исчерпывающий алгоритм (ETS):

1. Образуем перестановки первых n-1 чисел

2. Выбираем первую перестановку, строим соостветствующий путь и вычисляем его стоимость. Принимаем данную стоимость за минимальную.

3. Выбираем перестановку, строим соостветствующий путь и вычисляем его стоимость.

4. Сравниваем стоимость текущего пути с минимальной. Запоминаем минимальную из них. Возвращаемся к шагу 3.

Такой алгоритм называется исчерпывающим или переборным алгоритмом.

Проверка правильности алгоритма.

Это один из наиболее трудных этапов. Проверка правильности алгоритма часто заменяется проверкой правильности программы, то есть прогонкой её на различных тестах. Если выданные программой ответы могут быть подтверждены известными или вычисленными вручную данными, возникает искушение сделать вывод, что программа работает. Для большинства алгоритмов очень сложно составить систему тестов, проверяющую все особенности, тонкости работающей программы. 3% ошибок считается нормой. В документации должны быть описаны ситуации возникновения ошибок (ограничения).