Лабораторная работа
“Изучение основных законов и соотношений в цепях постоянного тока”
Цель работы: Изучение основных законов и соотношений электрических цепей постоянного тока.
ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ
Закон Ома
Закон Ома для электрической цепи. Электрический ток может возникнуть в замкнутой электрической цепи только под действием э. д. с., создаваемой источником электрической энергии (рисунок 1). В электрических схемах направление э. д. с. обозначают стрелкой от отрицательного зажима источника электрической энергии к положительному. В то же время направление напряжения обозначают стрелкой от положительного зажима источника электрической энергии или приемника к отрицательному. В некоторых случаях линией с двумя стрелками показывают узлы электрической цепи, между которыми приложено данное напряжение.

Рисунок 1 – Ток, э. д. с. и напряжение в замкнутой электрической цепи
Закон Ома устанавливает связь между э. д. с. Е источника электрической энергии, сопротивлением r и силой тока I в электрической цепи. Согласно этому закону
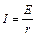 (1)
(1)
Полное сопротивление всей замкнутой электрической цепи можно представить в виде суммы двух сопротивлений: сопротивления внешней цепи rвн (например, какого-либо приемника электрической энергии) и внутреннего сопротивления r0 источника электрической энергии. Поэтому сила тока
 (2)
(2)
Чем больше э. д. с. Е источника и чем меньше сопротивление электрической цепи, тем больший ток проходит по этой цепи.
Закон Ома для участка электрической цепи. Закон Ома может быть применен не только ко всей цепи, но и к любому ее участку. В этом случае э. д. с. Е источника в формуле (7) должна быть заменена разностью потенциалов между началом и концом рассматриваемого участка, т. е. напряжением U, а вместо сопротивления всей цепи в формулу должно быть подставлено сопротивление данного участка:
 (3)
(3)
Законы Кирхгофа
Закон Ома определяет зависимость между силой тока, напряжением и сопротивлением для простейшей электрической цепи, представляющей собой один замкнутый контур. В практике встречаются более сложные (разветвленные) электрические цепи, в которых имеются несколько замкнутых контуров и несколько узлов, к которым сходятся токи, проходящие по ветвям. Значения силы токов и напряжений для таких цепей можно находить при помощи законов Кирхгофа.
Первый закон Кирхгофа (закон для токов). Согласно этому закону сумма токов, направленных к узлу электрической цепи, равна сумме токов, направленных от него (рисунок 2). Например, для узла А имеем:
 (4)
(4)
Преобразуя это уравнение, получим
 (5)
(5)
т. е. алгебраическая сумма токов в любом узле электрической цепи равна нулю. При этом значения токов, направленных к узлу А, считаются положительными, а значения токов, направленных от него, - отрицательными.

Рисунок 2 – Разветвленная электрическая цепь
Второй закон Кирхгофа (закон для напряжений). Согласно этому закону во всяком замкнутом электрическом контуре алгебраическая сумма э. д. с. равна алгебраической сумме напряжений на сопротивлениях, входящих в этот контур. При составлении формул, характеризующих второй закон Кирхгофа, значения э. д. с. и напряжений (Ir) считают положительными, если направления э. д. с. и токов на соответствующих участках контура совпадают с произвольно выбранным направлением обхода контура. Если же направления э. д. с. и токов на соответствующих участках контура противоположны выбранному направлению обхода, то значения таких э. д. с. и напряжений принимаются отрицательными.
Рассмотрим в качестве примера электрическую цепь (рисунок 3 а), в которой имеются два источника с электродвижущими силами E1 и Е2 и внутренними сопротивлениями r01 и r02 и два сопротивления r1 и r2. Применяя второй закон Кирхгофа для этой цепи, получим при обходе ее по показанной на рисунке 10 стрелке:


Рисунок 3 – Схемы электрической цепи с несколькими сопротивлениями и источниками э. д. с.:
а – неразветвленной, б - разветвленной
При этом э. д. с. Е1 и ток I совпадают с выбранным направлением обхода контура и их значения считаются положительными, а значение э. д. с. Е2, противоположной этому направлению, считается отрицательным.
Для электрической цепи (рисунок 3 б), по отдельным участкам которой проходят различные по силе токи I1 и I2, согласно второму закону Кирхгофа, имеем:
 .
.
Значения э. д. с. Е1 и тока I1 в этом уравнении считаются положительными (совпадают с принятым направлением обхода контура), а э. д. с. Е2 и тока I2 – отрицательными.
Способы соединения приемников электрической энергии
В большинстве случаев приемники электрической энергии, включенные в цепь постоянного тока, можно рассматривать как идеализированные резисторы, имеющие то же электрическое сопротивление, что и реальный приемник. Это обстоятельство дает возможность при составлении и изучении электрических схем вместо конкретных приемников рассматривать соответствующие идеализированные резисторы (сопротивления), не учитывая их конструкции. Различают следующие способы соединения сопротивлений: последовательное, параллельное и смешанное.
Последовательное соединение. При последовательном соединении нескольких сопротивлений конец первого сопротивления соединяется с началом второго, конец второго – с началом третьего и т. д. (рисунок 4).

Рисунок 4 – Последовательное соединение сопротивлений
При таком соединении ток одинаковой силы проходит по всем сопротивлениям цепи. Согласно второму закону Кирхгофа, можно написать:

Так как напряжения на отдельных участках цепи по закону Ома
 ;
; 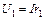 ;
;  ;
; 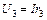 ,
,
то
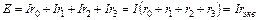 (5)
(5)
Следовательно, эквивалентное сопротивление цепи равно сумме всех последовательно соединенных сопротивлений:
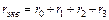 (6)
(6)
Напряжение U на зажимах источника в цепи с последовательно соединенными сопротивлениями равно сумме напряжений на каждом из них; например, при трех сопротивлениях
 (7)
(7)
Из указанных выше формул следует также, что напряжения распределяются между последовательно соединенными сопротивлениями пропорционально величинам их электрических сопротивлений:
 (8)
(8)
т. е. чем больше величина какого-либо сопротивления в последовательной цепи, тем большее напряжение приложено к нему.
Если последовательно соединяется несколько, например n, одинаковых сопротивлений r, то эквивалентное сопротивление цепи

напряжение U1 на каждом сопротивлении

Параллельное соединение. Несколько сопротивлений, соединенных параллельно, включаются между двумя узлами электрической цепи, образуя параллельные ветви. Например, три сопротивления r1, r2, r3 (рисунок 5), соединенных параллельно, включены в три параллельные ветви.

Рисунок 5 – Параллельное соединение сопротивлений
При параллельном соединении все сопротивления имеют одинаковое напряжение U. Поэтому согласно закону Ома,
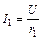 ;
;  ;
; 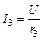 .
.
Общий ток согласно первому закону Кирхгофа
 ,
,
или
 (9)
(9)
Следовательно, эквивалентное сопротивление при параллельном соединении определяется формулой
 (10)
(10)
Заменяя электрические сопротивления обратными величинами – проводимостями 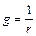 , получим, что общая проводимость при параллельном соединении равна сумме проводимостей отдельных ветвей, т. е.
, получим, что общая проводимость при параллельном соединении равна сумме проводимостей отдельных ветвей, т. е.
 (11)
(11)
Таким образом, при увеличении числа параллельно включаемых сопротивлений эквивалентная проводимость электрической цепи увеличивается, а эквивалентное сопротивление уменьшается.
Из приведенных формул следует, что токи распределяются между отдельными ветвями обратно пропорционально их электрическим сопротивлениям, или прямо пропорционально их проводимостям, например, при трех сопротивлениях
 .
.
Если параллельно соединяются несколько, например n, одинаковых сопротивлений r, то эквивалентное сопротивление цепи  , а ток In, проходящий по каждой ветви,
, а ток In, проходящий по каждой ветви,  .
.
При параллельном соединении приемники электрической энергии находятся под одним и тем же напряжением, и режим работы каждого из них не зависит от остальных. При выключении или обрыве провода в любом из приемников остальные приемники остаются включенными и продолжают нормально работать, в то время как при последовательном соединении приемников с изменением сопротивления одного из них изменяется напряжение на других приемниках. При выключении или обрыве электрической цепи в одном из приемников в остальных последовательно включенных приемниках прекращается ток. Поэтому параллельное соединение приемников получило наиболее широкое распространение. В частности, электрические лампы и двигатели обычно включаются параллельно.
Последовательное соединение приемников электрической энергии применяют в том случае, когда напряжение источника электрической энергии больше номинального напряжения, на которое рассчитан каждый приемник.
Смешанное соединение. При смешанном соединении часть сопротивлений включается последовательно, а часть – параллельно. Так, например, в схеме (рисунок 6 а) сопротивления rl и r2 включены последовательно, параллельно им включено сопротивление r3, а сопротивление r4 включено последовательно с группой сопротивлений r1 r2 и r3.

Рисунок 6 – Смешанное соединение сопротивлений:
а – схема, б, в – эквивалентные схемы
Определение эквивалентного сопротивления при смешанном соединении производят поэтапно. Например, для схемы (рисунок 6 а) вначале определяют эквивалентное сопротивление r12 последовательно включенных сопротивлений r1 и r2, т. е.  , при этом схема рисунка 6 а заменяется эквивалентной схемой рисунка 6 б. Затем определяют суммарное сопротивление r123 параллельно включенных сопротивлений r12 и r3 по формуле
, при этом схема рисунка 6 а заменяется эквивалентной схемой рисунка 6 б. Затем определяют суммарное сопротивление r123 параллельно включенных сопротивлений r12 и r3 по формуле

при этом схема рисунка 6 б заменяется эквивалентной схемой рисунка 6 в. После этого находят эквивалентное сопротивление всей цепи суммированием сопротивления r123 и последовательно включенного с ним сопротивления r4:
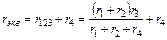
Следовательно, любое смешанное соединение сопротивлений последовательными этапами с использованием формул для последовательного и параллельного соединения сопротивлений может быть приведено к одному эквивалентному сопротивлению.
Схема электрического моста. При электрических измерениях, а также в некоторых других случаях сопротивления включают, как показано на рисунке 7. Такую схему называют схемой электрического моста или мостовой схемой.

Рисунок 7 – Схема электрического моста
Сопротивления r1 r2 r3 и r4 образуют так называемые плечи моста; участки цепи, соединяющие точки а и с, а также b и d, называют диагоналями моста. Обычно в одну диагональ, в данном случае а – с (питающая диагональ), подключается источник электрической энергии; в другую диагональ b – d (измерительная диагональ) включают электроизмерительный прибор или какой-либо регистрирующий аппарат. Если включить в диагональ b – d какое-либо сопротивление r и подобрать сопротивления плеч моста так, чтобы потенциалы точек b и d были одинаковыми, то сила тока I, протекающего через сопротивление r, будет равна нулю. Такой мост называется уравновешенным.
Для равновесия моста необходимо, чтобы напряжения
 и
и 
или же
 и
и 
В уравновешенном мосту  и
и  , так как
, так как  .
.
Следовательно, мост будет уравновешен при равенстве произведений сопротивлений противоположных его плеч:
 .
.
При несоблюдении этого условия через сопротивление r будет проходить ток I; такой мост называется неуравновешенным.






