Литература: Б-1, Б-2; О-1-4; Д-1-3
План лекции 3
1. Изучение методов расчета по кредитной карточке и процентов по кредиту.
2. Ежемесячный возврат части кредита с уплатой процентов (метод1)
3. Аннуитетный платеж (метод 2)
4. Единовременный возврат кредита с периодической уплатой процентов (Метод 3)
5. Вычисление параметров ссуды с нерегулярными платежами.
6. Формулы расчета процентов по кредиту в Excel.
План практического занятия 4
1. Расчеты по кредитной карточке.
2. Методы расчета процентов по кредиту.
Вопросы для самопроверки:
1. Как рассчитать ежемесячный возврат части кредита с уплатой процентов.
2. Как рассчитывается аннуитетный платеж.
3. Как рассчитывается единовременный возврат кредита с периодической уплатой процентов.
Темы эссе:
1. Как производятся расчеты по кредитной карточке.
2.Приведите конкретный пример использования формул расчета процентов по кредиту.
3. Опишите методы расчета процентов по кредиту.
Практические задания:
Пример 1. Допустим, у Вас есть кредитная карточка с определенной начальной суммой и Вы хотите узнать, на сколько месяцев хватит Вам этой суммы, если ежемесячно снимать с нее такое-то количество денег. На рис. 1 показан рабочий лист, на котором выполняются вычисления такого типа.
Рис. 1. Рабочий лист для расчетов по кредитной карточке
В диапазоне В1:В5 записаны входные данные по кредитной карточке. Например, начальная сумма на кредитной карточке составляет 10 000 руб., годовая процентная ставка равна 18,25%. Здесь принято, что минимальная сумма платежа составляет 2% от суммы, хранимой на карточке, т.е. в данном случае Вы можете снять не меньше 200 руб. Предположим, что такую сумму Вы и рассчитываете снимать ежемесячно (число в ячейке В5). Конечно, Вы можете ежемесячно снимать и другую сумму, не меньшую 200 руб., например 500 руб. Для этого просто измените число в ячейке В5.
В диапазоне В7:В9 выполняются вычисления.
Формула, записанная в ячейке В7, вычисляет, на сколько месяцев Вам хватит суммы, хранящейся на кредитной карточке: =КПЕР(В2/12;В5,–В1;0). Здесь предполагается, что в конце вычисленного периода на карточке должен остаться нуль рублей, поэтому последний аргумент в функции КПЕР равен нулю.
Простая формула =В7*В5 в ячейке В8 вычисляет общую сумму, которую Вы можете снять с кредитной карточки с учетом начисленных процентов.
Формула =В8–В1 в ячейке В9 вычисляет сумму, начисленную по процентам.
В этом примере 10 000 руб. вы можете потратить за почти 95 месяцев (более 7 лет), если ежемесячно будете снимать минимальную сумму в 200 руб. За это же время вам будет начислено 8 932,93 руб. процентов. Конечно, эти вычисления предполагают, что за все время пользования карточкой на ее счет никаких поступлений не было.
На рис. 2 показаны дополнительные вычисления, связанные с кредитной карточкой. Например, если Вы захотите исчерпать начальную сумму за 12 месяцев, то здесь Вы можете подсчитать, что в этом случае ежемесячно можно снимать с карточки 917,99 руб. (ячейка В15), при этом Вы получите общую сумму 11 015,88 руб.; начисления по процентам составят 1 015,88 руб.
В ячейке В15 записана формула =ПЛТ($B$2/12;A15;–$B$1)
Рис. 2 - Дополнительные расчеты по кредитной карточке
Задание 1. Постройте таблицу дополнительных расчетов по кредитной карточке в соответствии с рис. 2. Результаты расчетов представьте в виде графиков.
Задание 2. Составьте в Excel график ежемесячного погашения кредита (рис. 3), расположив исходные данные в диапазоне ячеек A1:B5. Значения ячеек в диапазоне B9:E21 должны быть рассчитаны с использованием соответствующих формул и функций.
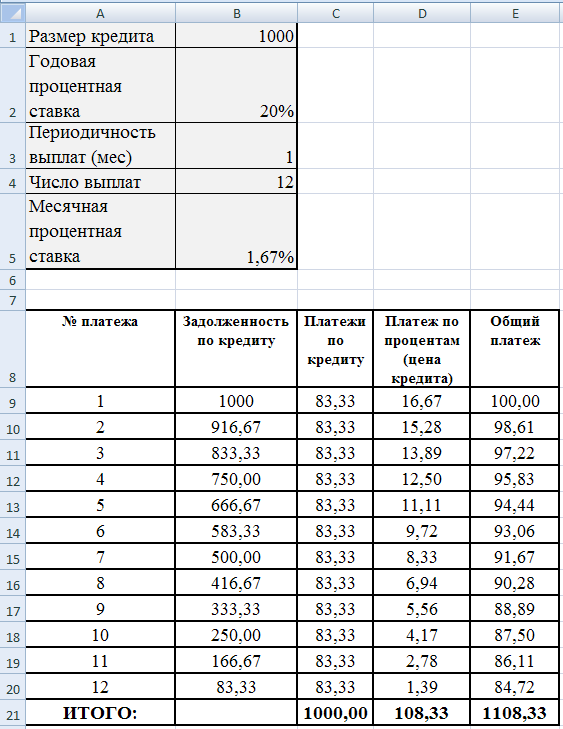
Рис. 3 - График ежемесячного погашения кредита
Задание 3. Составьте график погашения ссуды, представленный на рис. 4.
Параметры ссуды введены в диапазон В1:В4. Эти параметры используются в формулах, содержащихся в ячейках, начиная с девятой строки. В табл. 1 представлены формулы из строки 9 графика выплат. Формулы были скопированы во все остальные строки графика.
Рис. 4 - График выплат по ссуде
Таблица 1 – Расчетные формулы
| Ячейка | Формула | Описание |
| A9 | =A8+1 | Возвращает номер платежа |
| B9 | =ПЛТ($B$2*($B$3/12);$B$4;-$B$1) | Вычисляет размер выплаты |
| C9 | =C8+B9 | Возвращает общую (кумулятивную) сумму выплат |
| D9 | =ПРПЛТ($B$2*($B$3/12);A9;$B$4;-$B$1) | Вычисляет процентную часть выплаты |
| E9 | =E8+D9 | Вычисляет кумулятивную сумму выплат по процентам |
| F9 | =ОСПЛТ($B$2*($B$3/12);A9;$B$4;-$B$1) | Вычисляет основную часть выплаты |
| G9 | =G8+F9 | Вычисляет кумулятивную сумму основных выплат |
(Метод указания с практическими заданиями по дисциплине Компьютерный тренинг «Основы финансово-кредитного обслуживания фирм» 2014 г.)
Задания для самостоятельной работы:
Задание 1. Составьте график ежемесячного аннуитетного погашения кредита (рис. 5).
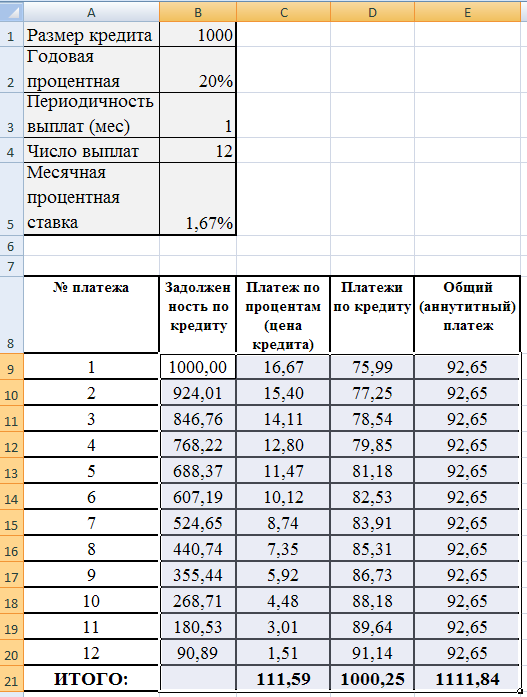
Задание 5. Постройте в Excel таблицу, представленную на рисунке 4 и заполните её в соответствии с таблицей 2
Таблица 2 - Формулы, используемые для вычисления параметров ссуды с нерегулярными платежами
| Ячейка | Формула | Описание |
| D6 | =ЕСЛИ(C6<>””;(C6-C5)/365*H5*ПС; “”) | По этой формуле вычисляется процент на основании даты платежа |
| E6 | =ЕСЛИ(C6<>””;B6-D6;””) | Чтобы получить основную часть платежа, из суммы платежа вычитается процентная часть |
| F6 | =ЕСЛИ(C6<>””;F5+B6;””) | Эта формула прибавляет сумму данного платежа к общей сумме |
| G6 | =ЕСЛИ(C6<>””; G5+D6;””) | Эта формула прибавляет процентную часть данного платежа к общей сумме |
| H6 | =ЕСЛИ(C6<>””;H5-E6;””) | Формула вычисляет остаток в конце каждого периода |
(Метод указания с практическими заданиями по дисциплине Компьютерный тренинг «Основы финансово-кредитного обслуживания фирм» 2014 г.)






