Лекция 5 Ряды динамики и их применение в анализе социально-экономических явлений
1. Ряды динамики и их виды.
2. Показатели динамического ряда.
3. Методы выявления основной тенденции развития.
Ряды динамики и их виды.
Ряд динамики – это ряд расположенных в хронологической последовательности статистических показателей, характеризующих изменение явления во времени.
Элементы ряда динамики.
1. Уровни ряда – это показатели, числовые значения которых составляют динамический ряд – У.
2. Момент времени – это период времени, к которому относится конкретный уровень динамического ряда – t.
 – ряд динамики.
– ряд динамики.
Классификация рядов динамики.
1. По времени.
а) Моментные ряды.
Характеризуют уровень какого-либо явления на определённый момент времени.
С помощью этих рядов анализируют динамику численности населения, ресурсов производства: ОПФ, земельных угодий, числа рабочих и других.
б) Интервальные ряды.
Характеризуют уровень явления за интервал времени.
С их помощью анализируют динамику объема производства, фонда заработной платы, объема товарооборота, числа родившихся и другие показатели.
2. По форме представления уровней.
А) Ряды абсолютных величин.
Пример: а) суммы продаж, млн. руб.; б) добычи нефти, млн. т.;
в) численности населения, млн. чел.
Б) Ряды относительных показателей.
Пример: а) доли городского и сельского населения; б) уровня безработицы; в) индексов цен.
В) Ряды средних величин.
Пример: а) средней зарплаты; б) урожайности; в) производительности.
3. По расстоянию между уровнями ряда.
А) Равноотстоящие.
Если уровни ряда представлены через равные следующие друг за другом интервалы времени.
Б) Нераноотстоящие.
Если уровни ряда представлены за неравномерные интервалы времени.
Правила построения динамических рядов.
1. Периодизация динамики.
Разделение ряда динамики во времени на однородные этапы, характеризующиеся одной закономерностью развития.
2. Сопоставимость статистических данных.
А) По территории.
Необходимо анализировать явление в одних и тех же территориальных единицах.
Б) По кругу охватываемых объектов.
Показатели динамического ряда должны быть однородны по экономическому содержанию и границам объекта.
Пример: При характеристике динамики численности студентов высших учебных заведений по годам нельзя в одни годы учитывать только численность студентов дневного отделения, а в другие численность студентов всех видов обучения.
В) По времени регистрации.
Для интервальных рядов должно обеспечиваться равенство периодов времени, за которые приводятся данные (нельзя сравнивать квартальную продукцию с годовой).
Для моментных рядов показатели следует приводить на одну и ту же дату.
Г) По единицам измерения.
Уровни динамического ряда должны выражаться в одинаковых единицах измерения, а стоимостные показатели в сопоставимых ценах.
Д) По методологии расчета.
Необходимо сравнивать показатели, рассчитанные по единой методике.
Пример:
Если в одни годы средняя урожайность сельскохозяйственных культур рассчитывалась с засеянной площади, а в другие с убранной. Или в одни годы производительность труда в промышленности определялась в расчете на 1 работника, а в другие – на одного работника промышленно-производственного персонала. В этих случаях необходимо показатели пересчитать по единой методике.
3. Упорядоченность рядов динамики во времени.
Замена пропусков уровней их расчетными показателями. Расчет недостающих уровней динамического ряда осуществляется при помощи метода интерполяции.
2. Показатели динамического ряда.
Абсолютные и относительные показатели:
1. Абсолютный прирост – ∆ у.
а) базисный:
∆ уiб = уi – у0i, где (1)
уi – сравниваемый i-й уровень ряда;
у0i – уровень, принятый за постоянную базу сравнения.
б) цепной:
∆ уiц = уi – уi - 1, где (2)
уi – 1 – уровень предшествующий i-му уровню ряда.
2. Темп роста - Тр.
а) базисный:
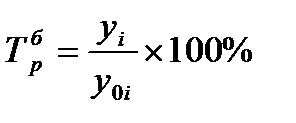 (3)
(3)
б) цепной:
 (4)
(4)
3. Темп прироста – Тпр.
а) базисный:
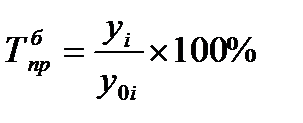 (5)
(5)
б) цепной:
 (6)
(6)
Если определён показатель темпа роста, то темп прироста можно рассчитать:
Тпр = Тр – 100 %
4. Абсолютное значение 1 процента прироста – А.
 (7)
(7)
Средние показатели динамического ряда.
Средний уровень динамического ряда.
А) В моментных рядах динамики с равноотстоящими уровнями средний уровень определяется по формуле средней хронологической:
 (8)
(8)
Б) В моментных рядах динамики с неравноотстоящими уровнями – по формуле:
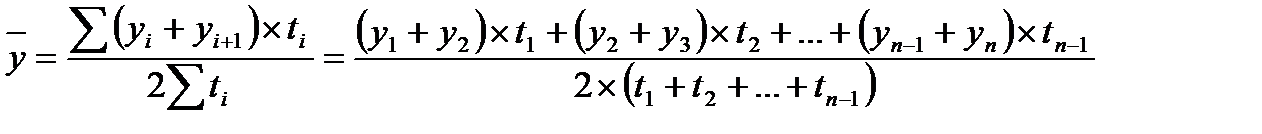 (9)
(9)
ti – длительность интервалов времени между уровнями.
В) В интервальных рядах с равноотстоящими уровнями – по средней арифметической простой:
 (10)
(10)
Г) В интервальных рядах с неравноотстоящими уровнями – по средней арифметической взвешенной:
 (11)
(11)






