Задача 1. Известно, что генеральная совокупность имеет распределение Пуассона 
, неизвестным является параметр λ. Используя указанный ниже метод получения точечных оценок, найти по выборке (x1,x2,….x8) оценку 
неизвестного параметра λ.
1. Метод моментов.
2. Метод максимального правдоподобия.
(См. исходные данные)
Задача 2. Известно, что генеральная совокупность имеет биномиальное распределение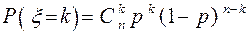 
, неизвестным является параметр p. Используя указанный ниже метод получения точечных оценок, найти по выборке (x1,x2,….x8) оценку 
неизвестного параметра p.
1. Метод максимального правдоподобия.
2. Метод моментов.
(См. исходные данные)
Задача 3. Генеральная совокупность имеет нормальное распределение с неизвестным математическим ожиданием aи известной дисперсией σ2. По выборке (x1,x2,…xn) объёма n вычислено выборочное среднее 
. Определить доверительный интервал для неизвестного математического ожидания, отвечающей заданной доверительной вероятности р.
(См. исходные данные)
Задача 4. Генеральная совокупность имеет нормальное распределение с неизвестными математическим ожиданием и дисперсией σ2. По выборке (x1,x2,…xn) объёма n вычислены оценки математического ожидания и дисперсии – выборочное среднее и исправленная выборочная дисперсия s2. Найти доверительный интервал для математического ожидания, отвечающей заданной доверительной вероятности р.
(См. исходные данные).
Задача 5. В результате n опытов получена несмещенная оценка в виде исправленной выборочной дисперсии s2для дисперсии нормальной генеральной совокупности. Найти доверительный интервал для дисперсии при доверительной вероятности р.
(См. исходные данные)
Задача 6. В серии из n выстрелов по мишени наблюдалось m попаданий. Найти доверительный интервал для вероятности р попадания в мишень при доверительной вероятности р.
(См. исходные данные)
Задача 7. В серии из n опытов событие А не наступило ни разу. Определить число опытов n, при котором верхняя доверительная граница для вероятности Р(А) равна заданному числу р1.Доверительную вероятность принять равной 0.95.
(См. исходные данные)
Задача 8. Для контроля взяты 200 узлов, собранных на заводском конвейере Число узлов miпри сборке которых пропущено i операций, сведено в таблицу:
| i | |||||||||
| mi | Всего 200 |
Согласуются ли полученные результаты с распределением Пуассона
, 
- случайное число пропущенных операций)по критерию 
при уровне значимости α? Решить задачу для заданного значения параметра λ и для случая, когда параметр λ оценивается по выборке.
(См. исходные данные)
Исходные данные
| № Вар. | Задача 1, 2 | Задача 3 | |||||||||||
| X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | n |
| n | σ2 | P | |
| 0.95 | |||||||||||||
| 0.94 | |||||||||||||
| 0.93 | |||||||||||||
| 0.92 | |||||||||||||
| 0.95 | |||||||||||||
| 0.94 | |||||||||||||
| 0.93 | |||||||||||||
| 0.92 | |||||||||||||
| 0.94 | |||||||||||||
| 0.93 | |||||||||||||
| 0.92 | |||||||||||||
| 0.95 | |||||||||||||
| 0.94 | |||||||||||||
| 0.93 | |||||||||||||
| 0.92 | |||||||||||||
| 0.95 | |||||||||||||
| 0.93 | |||||||||||||
| 0.92 | |||||||||||||
| 0.95 | |||||||||||||
| 0.94 | |||||||||||||
| 0.93 | |||||||||||||
| 0.92 | |||||||||||||
| 0.95 | |||||||||||||
| 0.94 | |||||||||||||
| 0.92 | |||||||||||||
| 0.95 | |||||||||||||
| 0.94 | |||||||||||||
| 0.93 | |||||||||||||
| 0.92 | |||||||||||||
| 0.95 | |||||||||||||
| 0.94 |
| № Вар | Задача 4 | Задача 5 | Задача 6 | Задача 7 | Задача 8 | |||||||
|
| s2 | n | р | n | s2 | р | n | m | p1 | a | α | |
| 2.1 | 0.5 | 0.8 | 0.98 | 0.01 | 1.70 | 0.002 | ||||||
| 2.1 | 0.5 | 0.9 | 1.5 | 0.98 | 0.02 | 1.71 | 0.01 | |||||
| 2.1 | 0.5 | 0.95 | 0.8 | 0.03 | 1.72 | 0.005 | ||||||
| 2.1 | 0.5 | 0.98 | 0.2 | 0.98 | 0.04 | 1.73 | 0.01 | |||||
| 1.7 | 0.8 | 0.8 | 0.96 | 0.05 | 1.74 | 0.05 | ||||||
| 1.7 | 0.8 | 0.9 | 0.96 | 0.06 | 1.75 | 0.005 | ||||||
| 1.7 | 0.8 | 0.95 | 0.8 | 0.07 | 1.76 | 0.02 | ||||||
| 1.7 | 0.8 | 0.98 | 0.96 | 0.08 | 1.77 | 0.002 | ||||||
| 2.1 | 0.5 | 0.9 | 0.8 | 0.09 | 1.78 | 0.01 | ||||||
| 2.1 | 0.5 | 0.95 | 0.9 | 0.011 | 1.79 | 0.2 | ||||||
| 2.1 | 0.5 | 0.98 | 0.98 | 0.012 | 1.80 | 0.05 | ||||||
| 2.1 | 0.5 | 0.8 | 0.9 | 0.013 | 1.81 | 0.01 | ||||||
| 1.7 | 0.8 | 0.9 | 0.8 | 0.014 | 1.82 | 0.02 | ||||||
| 1.7 | 0.8 | 0.95 | 0.96 | 0.015 | 1.83 | 0.002 | ||||||
| 1.7 | 0.8 | 0.98 | 0.98 | 0.016 | 1.84 | 0.1 | ||||||
| 1.7 | 0.8 | 0.8 | 0.8 | 0.017 | 1.85 | 0.01 | ||||||
| 2.1 | 0.5 | 0.95 | 0.8 | 0.018 | 1.86 | 0.02 | ||||||
| 2.1 | 0.5 | 0.98 | 0.96 | 0.019 | 1.87 | 0.01 | ||||||
| 2.1 | 0.5 | 0.8 | 3.5 | 0.98 | 0.02 | 1.88 | 0.005 | |||||
| 2.1 | 0.5 | 0.9 | 0.96 | 0.021 | 1.89 | 0.02 | ||||||
| 1.7 | 0.8 | 0.95 | 0.9 | 0.022 | 1.90 | 0.1 | ||||||
| 1.7 | 0.8 | 0.98 | 0.9 | 0.023 | 1.76 | 0.005 | ||||||
| 1.7 | 0.8 | 0.8 | 0.96 | 0.024 | 1.77 | 0.05 | ||||||
| 1.7 | 0.8 | 0.9 | 0.9 | 0.025 | 1.78 | 0.02 | ||||||
| 2.1 | 0.5 | 0.98 | 0.98 | 0.026 | 1.79 | 0.01 | ||||||
| 2.1 | 0.5 | 0.8 | 0.96 | 0.027 | 1.80 | 0.02 | ||||||
| 2.1 | 0.5 | 0.9 | 0.8 | 0.028 | 1.81 | 0.05 | ||||||
| 2.1 | 0.5 | 0.95 | 0.8 | 0.029 | 1.82 | 0.01 | ||||||
| 1.7 | 0.8 | 0.98 | 0.9 | 0.03 | 1.83 | 0.05 | ||||||
| 1.7 | 0.8 | 0.8 | 0.96 | 0.031 | 1.84 | 0.02 | ||||||
| 1.7 | 0.8 | 0.9 | 0.98 | 0.032 | 1.85 | 0.05 |
