Структурный анализ механизма
Примем следующие условные обозначения звеньев механизма: O и С – стойки; 1 – кривошип OA; 2 – шатун AB; 3 –коромысло CD; 4 – шатун DE; 5 – ползун E.
Количество подвижных звеньев  = 5.
= 5.
Кинематические пары: 1) стойка – кривошип OA; 2) кривошип OA – шатун AB; 3) шатун AB - коромысло CD; 4) коромысло CD – стойка; 5) коромысло CD – шатун DE; 6) шатун DE – ползун E; 7) ползун E – стойка; все пары низшие, плоские, накладывающие по 2 связи на относительное движение звеньев; количество пар 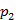 = 7.
= 7.
Степень подвижности механизма проверяем по формуле:
 = 3
= 3  5 – 2
5 – 2  7 = 1
7 = 1
Составим структурные группы механизма и определим класс и порядок:
1) стойка – кривошип OA – механизм I класса; 2) шатун AB - коромысло CD – группа II класса 1-го порядка; 3) шатун DE – ползун E – группа II класса 2-го порядка.
Формула строения механизма: I  II1
II1  II2.
II2.
механизм I классаf
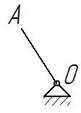
Структурная группа II1

Структурная группа II2

Кинематическое исследование механизма методом планов
Основные исходные данные
| Основные размеры (длины звеньев) в метрах | масштабный коэффициент  м/мм
м/мм
| Отрезки схемы соответствующих звеньев в миллиметрах | ||

| 0,15 | 0,004 | OA | |

| 0,7 | AB | ||

| 0,4 | CB | ||

| 0,8 | CD | ||

| 0,7 | ED | ||

| 0,6 | a | ||
| b | 0,72 | b |
 = 105 об/мин
= 105 об/мин
Для построения планов положений механизма переведём основные размеры в мм схемы: для этого назначаем масштабный коэффициент  :
:
 = 38 мм, ⇒
= 38 мм, ⇒  =
= 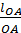 =
=  = 0,004 м/мм
= 0,004 м/мм
Строим план механизма в 8 положениях методом засечек.
Построение планов скоростей
Рассмотрим 1 положение
Определяем угловую скорость кривошипа  –
–  :
:
 = 11
= 11 
1)  т.к. они не подвижны
т.к. они не подвижны
2  Найдем скорость точки
Найдем скорость точки  : (принадлежит звену 1-кривошипу)
: (принадлежит звену 1-кривошипу)
 = 0,15 · 11 = 1,65 м/с; (⊥
= 0,15 · 11 = 1,65 м/с; (⊥  в сторону направления
в сторону направления  )
)
Произвольно выбираем точку  – полюс. Скорость полюса равна 0, а значит и все точки, скорость которых равна 0, находится в полюсе. Задаем отрезок схемы соответствующий вектору скорости точки
– полюс. Скорость полюса равна 0, а значит и все точки, скорость которых равна 0, находится в полюсе. Задаем отрезок схемы соответствующий вектору скорости точки  :
:
 ⇒ зададим масштабный коэффициент плана скоростей:
⇒ зададим масштабный коэффициент плана скоростей:
 =
= 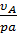 =
=  = 0,033
= 0,033 
3) Найдем скорость точки  (центр масс звена 1) из подобия:
(центр масс звена 1) из подобия:
 ⟹
⟹  = 0,5 · 50 = 25 мм
= 0,5 · 50 = 25 мм
 = 25 · 0,033 = 0,825 м/с;
= 25 · 0,033 = 0,825 м/с;
4) Найдем скорость точки  (принадлежит звену 2-шатуну и коромыслу 3)
(принадлежит звену 2-шатуну и коромыслу 3)

 = 46 · 0,033 = 1,564 м/с (относительная)
= 46 · 0,033 = 1,564 м/с (относительная)
 = 32 · 0,033 = 1,088 м/с (абсолютная)
= 32 · 0,033 = 1,088 м/с (абсолютная)
5) Найдем скорость точки  (центр масс звена 2) из подобия:
(центр масс звена 2) из подобия:
 ⟹
⟹  = 0,5 · 46 = 23 мм
= 0,5 · 46 = 23 мм
 = 35 · 0,034 = 1,190 м/с;
= 35 · 0,034 = 1,190 м/с;
6) Найдем скорость точки  из подобия:
из подобия:
 ⟹
⟹  =
=  · 32 = 64 мм
· 32 = 64 мм
 = 64 · 0,033 = 1,7 м/с;
= 64 · 0,033 = 1,7 м/с;
7) Найдем скорость точки  (центр масс звена 3) из подобия:
(центр масс звена 3) из подобия:
 ⇒
⇒  =
=  · 64 = 32 мм
· 64 = 32 мм
 = 32 · 0,033 = 1,088 м/с;
= 32 · 0,033 = 1,088 м/с;
8) Найдем скорость точки  : (принадлежит звену 5 – ползуну)
: (принадлежит звену 5 – ползуну)
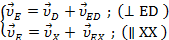
 = 20 · 0,033 = 0,680 м/с (относительная)
= 20 · 0,033 = 0,680 м/с (относительная)
 =61 · 0,033 = 2,074 м/с (абсолютная)
=61 · 0,033 = 2,074 м/с (абсолютная)
9) Найдем скорость точки  (центр масс звена 4)
(центр масс звена 4)  из подобия:
из подобия:
 ⇒
⇒  = 0,5 · 20 = 10 мм
= 0,5 · 20 = 10 мм
 = 62 · 0,033 = 2,108 м/с
= 62 · 0,033 = 2,108 м/с
10) Найдем угловые скорости звеньев - ω:
 =
=  =
=  =
=  = 2,12
= 2,12 
Направление определяется, приложением вектора  с плана скоростей в точку B
с плана скоростей в точку B
 =
=  =
=  =
=  = 2,39
= 2,39 
Направление определяется, приложением вектора  с плана скоростей в точку B
с плана скоростей в точку B
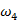 =
=  =
=  =
=  = 1,04
= 1,04 
Направление определяется, приложением вектора 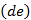 с плана скоростей в точку E
с плана скоростей в точку E
Результаты расчетов в остальных положениях механизма получены аналогичным способом и представлены в таблице 1.
Таблица 1
Значения длин отрезков с плана скоростей и скоростей характерных точек механизма.
| положения | 4’ | Ед изм | ||||||||
| значения | ||||||||||

| мм | |||||||||

| 1,65 | 1,65 | 1,65 | 1,65 | 1,65 | 1,65 | 1,65 | 1,65 | 1,65 | м/с |

| мм | |||||||||

| 0,825 | 0,825 | 0,825 | 0,825 | 0,825 | 0,825 | 0,825 | 0,825 | 0,825 | м/с |

| мм | |||||||||

| 1,65 | 1,485 | 0,924 | 0,165 | 1,023 | 1,650 | 2,673 | 1,353 | 1,155 | м/с |

| мм | |||||||||

| 0,000 | 0,957 | 1,650 | 1,716 | 0,726 | 0,000 | 1,716 | 2,244 | 1,122 | м/с |
| мм | |||||||||

| 0,825 | 1,122 | 1,584 | 1,683 | 1,155 | 0,825 | 1,023 | 1,848 | 1,353 | м/с |

| мм | |||||||||

| 0,000 | 1,914 | 3,300 | 3,432 | 1,452 | 0,000 | 3,432 | 4,488 | 2,244 | м/с |
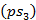
| мм | |||||||||

| 0,000 | 1,914 | 3,300 | 3,432 | 1,452 | 0,000 | 3,432 | 4,488 | 2,244 | м/с |
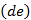
| мм | |||||||||
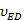
| 0,000 | 0,726 | 0,462 | 0,594 | 0,594 | 0,000 | 1,155 | 0,297 | 0,825 | м/с |

| мм | |||||||||

| 0,000 | 1,749 | 3,201 | 3,432 | 1,320 | 0,000 | 3,300 | 4,455 | 2,046 | м/с |

| мм | |||||||||

| 0,000 | 1,815 | 3,234 | 3,432 | 1,353 | 0,000 | 3,300 | 4,455 | 2,112 | м/с |

| с-1 | |||||||||

| 2,36 | 2,12 | 1,32 | 0,24 | 1,46 | 2,36 | 3,82 | 1,93 | 1,65 | с-1 |

| 0,00 | 2,39 | 4,13 | 4,29 | 1,82 | 0,00 | 4,29 | 5,61 | 2,81 | с-1 |
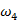
| 0,00 | 1,04 | 0,66 | 0,85 | 0,85 | 0,00 | 1,65 | 0,42 | 1,18 | с-1 |
Построение планов ускорений
Рассмотрим 4 положение
1)  т.к. они не подвижны
т.к. они не подвижны
2) Найдем ускорение точки  :
:
 ; где
; где  =
= 

 = const
= const 
 0 ⇒
0 ⇒  = 0 Таким образом получаем:
= 0 Таким образом получаем:
 =(11) 2
=(11) 2  0,15 = 18,15 м/с2 (направленно ∥ OA, от A к O)
0,15 = 18,15 м/с2 (направленно ∥ OA, от A к O)
Произвольно выбираем точку  –полюс. Ускорение полюса равно 0, а значит и все точки, ускорения которых равны 0, находятся в полюсе. Задаем отрезок схемы соответствующий вектору ускорения точки
–полюс. Ускорение полюса равно 0, а значит и все точки, ускорения которых равны 0, находятся в полюсе. Задаем отрезок схемы соответствующий вектору ускорения точки  :
:
 = 50 мм ⇒ зададим масштабный коэффициент плана ускорений:
= 50 мм ⇒ зададим масштабный коэффициент плана ускорений:
 =
=  = 0,363 м/с2
= 0,363 м/с2
3) Найдем ускорение точки  (центр масс звена 1) из подобия:
(центр масс звена 1) из подобия:
 ⟹
⟹  = 0,5 · 50 = 25 мм
= 0,5 · 50 = 25 мм
 = 25 · 0,363 = 9,075 м/с2
= 25 · 0,363 = 9,075 м/с2
4) Найдем ускорение точки  :
:

Нормальные ускорения:
 = (1,59)2
= (1,59)2  0,9 =2,28 м/с2 (нормальное)
0,9 =2,28 м/с2 (нормальное)
Переводим в мм схемы:
 =
=  =
=  = 5 мм (направленно ∥ BA, от B к A)
= 5 мм (направленно ∥ BA, от B к A)
 = (0,75)2
= (0,75)2  0,5 =0,28 м/с2 (нормальное)
0,5 =0,28 м/с2 (нормальное)
Переводим в мм схемы:
 =
= 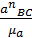 =
=  = 1 мм (направленно ∥ BC, от B к C) (точка т.к. < 2 мм)
= 1 мм (направленно ∥ BC, от B к C) (точка т.к. < 2 мм)
 = 12 · 0,4448 = 5,34 м/с2 (тангенциальное(касательное))
= 12 · 0,4448 = 5,34 м/с2 (тангенциальное(касательное))
 = 14 · 0,4448 = 6,23 м/с2 (относительное)
= 14 · 0,4448 = 6,23 м/с2 (относительное)
 = 45 · 0,4448 = 20,02 м/с2 (тангенциальное(касательное))
= 45 · 0,4448 = 20,02 м/с2 (тангенциальное(касательное))
 = 45 · 0,4448 = 20,02 м/с2 (абсолютное)
= 45 · 0,4448 = 20,02 м/с2 (абсолютное)
5) Найдем ускорение точки  из подобия:
из подобия:
 ⟹
⟹  = 0,5 · 14 = 7 мм
= 0,5 · 14 = 7 мм
 = 47 · 0,4448 = 20,91 м/с2
= 47 · 0,4448 = 20,91 м/с2
6) Найдем ускорение точки  из подобия:
из подобия:
 ⟹
⟹  =
=  · 45 = 90 мм
· 45 = 90 мм
 = 90 · 0,4448 = 40,03 м/с2
= 90 · 0,4448 = 40,03 м/с2
7) Найдем ускорение точки  из подобия:
из подобия:
 ⇒
⇒  =
=  · 90 = 45 мм
· 90 = 45 мм
 = 45 · 0,4448 = 20,02 м/с2
= 45 · 0,4448 = 20,02 м/с2
8) Найдем ускорение точки  :
:

 = (0,0,24)2
= (0,0,24)2  0,7 =0,04 м/с2
0,7 =0,04 м/с2
Переводим в мм схемы:
 =
=  =
=  = 0 мм, (точка т.к. < 2 мм) (направленно ∥ ED, от E к D)
= 0 мм, (точка т.к. < 2 мм) (направленно ∥ ED, от E к D)
 = 33 · 0,4448 = 14,68 м/с2 (тангенциальное(касательное))
= 33 · 0,4448 = 14,68 м/с2 (тангенциальное(касательное))
 = 33 · 0,4448 = 14,68 м/с2 (относительное)
= 33 · 0,4448 = 14,68 м/с2 (относительное)
 = 85 · 0,4448 = 37,81 м/с2 (абсолютное)
= 85 · 0,4448 = 37,81 м/с2 (абсолютное)
8) Найдем ускорение точки  (центр масс звена 4)
(центр масс звена 4)  из подобия:
из подобия:
 ⇒
⇒  = 0,5 · 33 = 16 мм
= 0,5 · 33 = 16 мм
 = 86 · 0,4448 = 38,25 м/с2
= 86 · 0,4448 = 38,25 м/с2
9) Найдем угловые ускорения звеньев - ε:
 т.к.
т.к.  = const
= const
 =
= 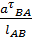 =
=  =
=  = 33,19
= 33,19 
Направление определяется, приложением вектора  с плана ускорений в точку B
с плана ускорений в точку B
 =
=  =
=  =
=  = 64,43
= 64,43 
Направление определяется, приложением вектора  с плана ускорений в точку B
с плана ускорений в точку B
 =
=  =
=  =
= 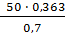 = 25,93
= 25,93 
Направление определяется, приложением вектора  с плана ускорений в точку Е
с плана ускорений в точку Е
Результаты расчетов в остальных пяти положениях механизма получены аналогичным способом и представлены в таблице 2
Таблица 2
Значения длин отрезков с плана ускорений и ускорений характерных точек механизма.
| положения | ед изм | |||
| значения | ||||

| мм | |||

| 18,15 | 18,15 | 18,15 | м/с2 |

| мм | |||

| 9,075 | 9,075 | 9,075 | м/с2 |

| мм | |||

| 3,90 | 1,49 | 1,91 | м/с2 |

| мм | |||

| 0,00 | 1,32 | 3,16 | м/с2 |

| мм | |||

| 3,27 | 23,23 | 21,05 | м/с2 |

| мм | |||

| 5,08 | 23,23 | 21,05 | м/с2 |

| мм | |||

| 14,52 | 25,77 | 15,97 | м/с2 |

| мм | |||

| 14,52 | 25,77 | 16,34 | м/с2 |

| мм | |||

| 16,34 | 18,88 | 13,43 | м/с2 |

| мм | |||

| 29,04 | 51,55 | 32,67 | м/с2 |
| мм | |||

| 29,04 | 51,55 | 32,67 | м/с2 |

| мм | |||

| 0,51 | 0,97 | м/с2 | |

| мм | |||

| 13,43 | 18,15 | 5,81 | м/с2 |

| мм | |||

| 13,43 | 18,15 | 5,81 | м/с2 |

| мм | |||

| 26,14 | 48,64 | 30,86 | м/с2 |

| мм | |||

| 26,86 | 49,37 | 31,58 | м/с2 |

| 4,67 | 33,19 | 30,07 | с-2 |

| 36,30 | 64,43 | 39,93 | с-2 |

| 19,19 | 25,93 | 8,30 | с-2 |
Построение кинематических диаграмм
Определяем перемещения S пятого звена (точка E) с плана механизма и уменьшаем в 2 раза. Зададим масштабный коэффициент
 · 3 = 0,004м/мм · 3 = 0,012 м/мм
· 3 = 0,004м/мм · 3 = 0,012 м/мм
По оси абсцисс откладываем углы поворота кривошипа  , масштабный коэффициент будет:
, масштабный коэффициент будет:
 = 0,026 рад/мм
= 0,026 рад/мм
Масштаб времени
 = 0,0024 с/мм
= 0,0024 с/мм
Далее методом графического дифференцирования(метод хорд) строим диаграммы скорости и ускорения. Масштабы по осям ординат определим по формулам:
Для диаграммы скоростей:
 = 0,143
= 0,143 
Для диаграммы ускорений:
 = 2,383
= 2,383 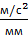
Где Н – произвольное полюсное расстояние
Аналогичным методом строим диаграммы изменения угловой скорости и ускорения звена 4 в функции угла поворота кривошипа.
Для этого по оси абсцисс откладываем угол поворота кривошипа, а по оси ординат будут значения 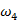 , далее графическим дифференцированием получаем диаграмму изменения угловой скорости звена 4 –
, далее графическим дифференцированием получаем диаграмму изменения угловой скорости звена 4 –  .Ординаты графика
.Ординаты графика 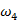 приведены в таблице 4
приведены в таблице 4
Масштабы диаграмм:
 = 0,0295 с-1/мм
= 0,0295 с-1/мм
 =
=  = 0,615 с-2/мм
= 0,615 с-2/мм
Таблица 4 Угловая скорость и ординаты графика
| 4' | |||||||||

| 0,00 | 1,04 | 0,66 | 0,85 | 0,85 | 0,00 | 1,65 | 0,42 | 1,18 |
| орд |
Построение годографа скорости
Строим годограф скорости центра масс  звена 2, перенося с построенных планов скоростей векторы
звена 2, перенося с построенных планов скоростей векторы  в общую точку. Соединяем концы векторов плавной лекальной кривой.
в общую точку. Соединяем концы векторов плавной лекальной кривой.
Определение погрешности расчетов
Скоростей точек
| положения | 4' | Ед изм | ||||||||
| значения | ||||||||||

| 0,000 | 1,735 | 3,234 | 3,315 | 1,298 | 0,000 | 3,279 | 4,428 | 2,076 | м/с |

| 0,000 | 1,749 | 3,201 | 3,432 | 1,320 | 0,000 | 3,300 | 4,455 | 2,046 | м/с |

| 0,00 | 3,31 | 1,04 | 0,76 | 4,41 | 0,00 | 0,57 | 0,84 | 0,44 | % |
Ускорений точек

| 25,87 | 47,16 | 31,24 | м/с2 |

| 26,14 | 48,64 | 30,86 | м/с2 |

| 5,57 | 2,15 | 6,09 | % |
Силовой расчет механизма
Рассмотрим 4 положение механизма.
Исходные данные:
| Веса звеньев: | Моменты инерции: | Усилие на ползун: |
 = 50 H = 50 H
|  = 0,03 кгм2 = 0,03 кгм2
|  = 2000 H = 2000 H
|
 = 140 H = 140 H
|  = 1 кгм2 = 1 кгм2
| |
 = 160 H = 160 H
|  = 1,2 кгм2 = 1,2 кгм2
| |
 = 100 H = 100 H
|  = 0,35 кгм2 = 0,35 кгм2
| |
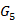 = 80 H = 80 H
|
1) Определение сил инерции звеньев –  .
.
 силы инерции приводятся к одной результирующей силе, приложенной в центре тяжести звена, и направленной противоположно ускорению центра тяжести звена.
силы инерции приводятся к одной результирующей силе, приложенной в центре тяжести звена, и направленной противоположно ускорению центра тяжести звена.
 =
=  =
= 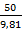 · 9,075 = 46,25 H
· 9,075 = 46,25 H
 =
=  · 18,88 = 269,44 H
· 18,88 = 269,44 H
 =
=  · 51,55 = 840,77 H
· 51,55 = 840,77 H
 =
=  · 49,37 = 503,26 H
· 49,37 = 503,26 H
 =
=  · 48,64 = 396,66 H
· 48,64 = 396,66 H
2) Определение моментов пары сил инерции звеньев – 
 моментов пары сил инерции звеньев направлены противоположно угловым ускорениям звеньев.
моментов пары сил инерции звеньев направлены противоположно угловым ускорениям звеньев.
 =
=  = 0 (т. к.
= 0 (т. к.  = const ⇒
= const ⇒  = 0)
= 0)
 = 1 · 33,19 = 33,19 Hм
= 1 · 33,19 = 33,19 Hм
 = 1,2 · 64,43 = 77,32 Hм
= 1,2 · 64,43 = 77,32 Hм
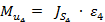 = 0,35 · 25,93 = 9,08 Hм
= 0,35 · 25,93 = 9,08 Hм
 = 0 (т к
= 0 (т к  = 0)
= 0)
3)Определение реакции в кинематических парах структурной группы второго класса второго вида (звенья 4 и 5).
Действие отброшенных звеньев заменено действием реакций  34 и
34 и  05 , которые необходимо определить. Разложим реакцию
05 , которые необходимо определить. Разложим реакцию  34 на две составляющие:
34 на две составляющие:
 – действующую вдоль звена DE
– действующую вдоль звена DE
 – действующую перпендикулярно звену DE;
– действующую перпендикулярно звену DE;
При этом 
Реакция  05 будет проходить через центр шарнира Е⊥ Х-Х (пара поступательная) так как все силы, действующие на звено 5, проходят через точку E.
05 будет проходить через центр шарнира Е⊥ Х-Х (пара поступательная) так как все силы, действующие на звено 5, проходят через точку E.
Порядок нахождения искомых реакций в структурной группе II2 представлен в табл. 5.
Таблица 5. Порядок силового расчета группы II2 (4;5)
| № П/П | Искомые реакции | Уравнения равновесия | Равновесие |

|  = 0 = 0
| Звена 4 | |
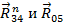
|  = 0 = 0
| Структурной группы 4 - 5 | |

|  = 0 = 0
| Звена 5 |
1. Величина  может быть непосредственно получена из уравнения равновесия звена 4.
может быть непосредственно получена из уравнения равновесия звена 4.
Звено 4 находится под действием следующих сил: веса  4 , силы инерции
4 , силы инерции 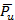 4 и момента
4 и момента  , составляющих
, составляющих  реакции
реакции  34 , и реакции
34 , и реакции  54 , которой заменено действие отсоединенного звена 5.
54 , которой заменено действие отсоединенного звена 5.
 = 0
= 0
Откуда
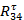 =
=  =
=  = 105,82 H
= 105,82 H
2. Составляем уравнение равновесия структурной группы, приравнивания нулю векторную сумму всех сил, действующих на группу II2:
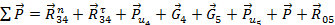 = 0
= 0
Для построения диады сил (плана сил) переведем силы, входящие в уравнение, в отрезки схемы:
Масштаб сил: 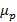 =
=  =
=  = 10 H/мм
= 10 H/мм
| Сила, Н | Масштаб сил, H/мм | отрезки плана, мм | |
| 10 H/мм | |||
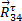
| 105,82 | ||

| 503,26 | ||

| |||
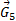
| |||

| 396,66 | ||

|
Начинаем строить план с точки 
Измерив отрезки с плана сил, получим искомые реакции:
 = 111 · 10 = 1110 H
= 111 · 10 = 1110 H
 = 11 · 10 = 1110 H
= 11 · 10 = 1110 H
 18 · 10 = 180 H
18 · 10 = 180 H

3. Реакция во внутренней кинематической паре определяется из условия равновесия звена 5:
 = 0
= 0
Из плана сил очевидно, что искомой реакцией будет отрезок 
 = 160 · 10 = 1600 H
= 160 · 10 = 1600 H

4) Определение реакций в структурной группе II1 (2;3)
Прикладываем в точке D силу  . Неизвестную силу
. Неизвестную силу  12 - реакция 1 звена (кривошипа) на 2 (шатун) раскладываем на две составляющие:
12 - реакция 1 звена (кривошипа) на 2 (шатун) раскладываем на две составляющие:  . Эта сила проходит через центр шарнира A, как всякая реакция во вращательной кинематической паре. неизвестную силу
. Эта сила проходит через центр шарнира A, как всякая реакция во вращательной кинематической паре. неизвестную силу  03 - реакция стойки на звено 3 (коромысло) раскладываем на две составляющие:
03 - реакция стойки на звено 3 (коромысло) раскладываем на две составляющие:  . Эта сила проходит через центр шарнира С, как всякая реакция во вращательной кинематической паре.
. Эта сила проходит через центр шарнира С, как всякая реакция во вращательной кинематической паре.
Порядок определения реакций приведен в таблице 6, и на соответствующих планах сил.
Таблица 6 Порядок силового расчета группы II1 (2;3)
| № П/П | Искомые реакции | Уравнения равновесия | Равновесие |

|  = 0 = 0
| Звена 2 | |

|  = 0 = 0
| Звена 3 | |

|  = 0 = 0
| Звенья 2 и 3 | |

|  = 0 = 0
| Звена 2 |
1. Сумма моментов всех сил звена 2 относительно точки B:
 = 0
= 0
Откуда
 =
=  =
=  = 60,5 H
= 60,5 H
2. Сумма моментов всех сил звена 3 относительно точки B:
 = 0
= 0
Откуда
 =
=  =
=  = 783,5 H
= 783,5 H
3. Из уравнения равновесия звеньев 2 и 3 определим реакции 
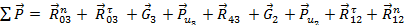 = 0
= 0
Для построения диады сил (плана сил) переведем силы входящие в уравнение в отрезки схемы:
Масштаб сил: 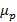 =
=  =
= 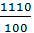 = 11,1 H/мм
= 11,1 H/мм
| Сила, Н | Масштаб сил, H/мм | отрезки плана, мм | |
| 11,1 H/мм | |||

| 783,5 | ||
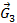
| |||

| 840,77 | ||

| |||

| |||

| 269,44 | ||

| 60,5 |
Измерив отрезки с плана сил, получим искомые реакции:
 = 3 · 11,1 = 33,3 H
= 3 · 11,1 = 33,3 H
 = 71 · 11,1 = 788,1 H
= 71 · 11,1 = 788,1 H
 = 79 · 11,1 = 876,9 H
= 79 · 11,1 = 876,9 H
 = 79 · 11,1 = 876,9 H
= 79 · 11,1 = 876,9 H
4. Из уравнения равновесия звена 2 определим реакцию  (реакция 3 звена на второе)
(реакция 3 звена на второе)
 = 0
= 0
Из плана сил очевидно, что искомой реакцией будет отрезок 
 = 98 · 11,1 = 1087,8 H
= 98 · 11,1 = 1087,8 H
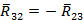
5) Силовой расчет механизма 1 класса.
Рассмотрим равновесие звена OA. К нему приложены силы:
В точке A – реакция  , в точке O реакция стойки
, в точке O реакция стойки  , в точке S1 – вес кривошипа
, в точке S1 – вес кривошипа 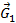 и
и 
1.Определим уравновешивающий момент  :
:
 = 0
= 0
 = 0,005 · (-50 · 29 + 876,9 · 19) = 76,06 Hм
= 0,005 · (-50 · 29 + 876,9 · 19) = 76,06 Hм
2.Из уравнения равновесия звена 1 определим реакцию  :
:
 = 0
= 0
Для построения диады сил (плана сил) переведем силы, входящие в уравнение, в отрезки схемы:
Масштаб сил: 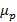 =
=  =
=  = 8,77 H/мм
= 8,77 H/мм






