Оба эти употребления ба существенно отличаются от его употребления в «Цзо чжуани». Здесь на место «восьми» не подставляется ни одна гексаграмма. Во втором фрагменте вообще фигурирует лишь одна единственная гексаграмма Тай (№11). В первом фрагменте указаны две гексаграммы, но термин ба со всей определенностью посредством квантороподобного распределителя подлежащего цзе отнесен к ним обеим. Кроме того, гексаграммы Чжунь (№3) и Юй (№16) различаются между собой тремя чертами (I, IV, V), что не отвечает принципу истолкования ба в «Цзо чжуани», согласно которому соответствующие гексаграммы должны совпадать или не совпадать в одной или пяти чертах.
Итак, достоверно известно, что ицзинистический термин ба обозначает гексаграммы, которые свободно могут не называться. Отсюда естественно заключить, что обозначаемые ба, но не называемые гексаграммы легко выводимы из предпосылаемых этому термину гексаграмм. Исходя из прямого смысла ба, нетрудно предположить, что он обозначает 8 гексаграмм. Данное предположение в свою очередь объясняет, почему в «Цзо чжуани» термин ба все-таки соотнесен с определенной гексаграммой. Подобная конкретизация требуется при необходимости выделения одной или нескольких гексаграмм из восьми.
Принадлежность каждой гексаграммы к какому-то набору из 8 гексаграмм является несомненным фактом, связанным с восьмеричностью всей совокупности 64 гексаграмм, членящихся на 8 триграмм. Внутреннюю закономерность гексаграммного ряда и в линейной последовательности и квадратном расположении Фу-си, и в мавандуйской последовательности, и в расположении 8 «дворцов» Цзин Фана (I в. до н.э.) (см. схему 12) составляет деление на восьмичленные блоки, идущие друг за другом. Хотя и без столь явного алгоритма, на 8 столбцов и 8 строк разбиты 64 гексаграммы в квадратном расположении Вэнь-вана. Однако исследуемый нами термин, видимо, обозначал не эти восьмерицы. Как кажется, стоящий за ним принцип предъявлен в уже не раз упоминавшемся ключевом фрагменте «Цзо чжуани» (Чжао, 29-й г.). Согласно этому принципу образуются восьмеричные наборы гексаграмм, включающие в себя две полярные гексаграммы, различающиеся всеми шестью чертами, и шесть промежуточных, совпадающих с полярными в одной или пяти чертах. Содержащаяся в данном фрагменте «Цзо чжуани» последовательность гексаграмм обнаруживает ясный алгоритм, с помощью которого, дополнив ее гексаграммами в квадратных скобках, мы получим два 8-членных набора: а)  №1,
№1,  №44,
№44,  №13, [
№13, [  №10,
№10,  №9],
№9],  №14,
№14,  №43,
№43,  №2 и б)
№2 и б)  №2,
№2,  №23, [
№23, [  №8,
№8,  №16,
№16,  №15,
№15,  №7,
№7,  №24,
№24,  №1]. В сумме они включают в себя все гексаграммы, необходимые для выделения каждой отдельной черты полярных гексаграмм Цянь (№1) и Кунь (№2) обоими возможными способами: привлечением гексаграммы с противоположной чертой в данной позиции или с противоположными чертами в остальных пяти позициях (последний способ здесь реализуется при считывании справа налево). Мы предполагаем, что именно такие наборы из 8 гексаграмм обозначались термином ба — «восемь» в «Цзо чжуани» и «Го юе». Связанный с этим термином фундаментальный нумерологический принцип воплощен в порядке триграмм, приписываемом Вэнь-вану (см. схему 4). В комментирующей части «Чжоу и» («Шо гуа чжуань», 8/10) данный порядок представлен разбитым на два ряда — мужских и женских триграмм, во главе которых стоят главные — отцовская и материнская триграммы Цянь и Кунь[47]z:\CorvDoc\infopedia2\shchu01\refer.htm - s48. Мужские триграммы: Цянь (Ц) — отец, Чжэнь (Ч) — старший сын, Кань (Ка) — средний сын, Гэнь (Г) — младший сын. Женские триграммы: Кунь (К) — мать, Сюнь (С) — старшая дочь, Ли (Л) — средняя дочь, Дуй (Д) — младшая дочь. Соотнесение с полом и старшинством основано на наличии у соответствующей триграммы одной одинаковой черты с отцовской (мужеобразующей) или материнской (женообразующей) триграммой в нижней (старшей), центральной (средней) или верхней (младшей) позиции. Эти «сыновья» и «дочери» в раздельном расположении между «отцом» и «матерью» образуют два 5-членных набора, по своему устройству (с учетом прямого и обратного считывания) идентичных двум вышеприведенным 8-членным наборам гексаграмм: а)
№1]. В сумме они включают в себя все гексаграммы, необходимые для выделения каждой отдельной черты полярных гексаграмм Цянь (№1) и Кунь (№2) обоими возможными способами: привлечением гексаграммы с противоположной чертой в данной позиции или с противоположными чертами в остальных пяти позициях (последний способ здесь реализуется при считывании справа налево). Мы предполагаем, что именно такие наборы из 8 гексаграмм обозначались термином ба — «восемь» в «Цзо чжуани» и «Го юе». Связанный с этим термином фундаментальный нумерологический принцип воплощен в порядке триграмм, приписываемом Вэнь-вану (см. схему 4). В комментирующей части «Чжоу и» («Шо гуа чжуань», 8/10) данный порядок представлен разбитым на два ряда — мужских и женских триграмм, во главе которых стоят главные — отцовская и материнская триграммы Цянь и Кунь[47]z:\CorvDoc\infopedia2\shchu01\refer.htm - s48. Мужские триграммы: Цянь (Ц) — отец, Чжэнь (Ч) — старший сын, Кань (Ка) — средний сын, Гэнь (Г) — младший сын. Женские триграммы: Кунь (К) — мать, Сюнь (С) — старшая дочь, Ли (Л) — средняя дочь, Дуй (Д) — младшая дочь. Соотнесение с полом и старшинством основано на наличии у соответствующей триграммы одной одинаковой черты с отцовской (мужеобразующей) или материнской (женообразующей) триграммой в нижней (старшей), центральной (средней) или верхней (младшей) позиции. Эти «сыновья» и «дочери» в раздельном расположении между «отцом» и «матерью» образуют два 5-членных набора, по своему устройству (с учетом прямого и обратного считывания) идентичных двум вышеприведенным 8-членным наборам гексаграмм: а) 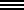 Ц,
Ц,  Ч,
Ч,  Ка,
Ка,  Г,
Г,  К и б)
К и б)  К,
К, 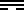 С,
С,  Л,
Л,  Д,
Д, 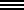 Ц. Примечательна также троично-пятеричная структура этих гексаграммных наборов, возможно, входившая в круг значений важного нумерологического термина сань у
Ц. Примечательна также троично-пятеричная структура этих гексаграммных наборов, возможно, входившая в круг значений важного нумерологического термина сань у 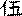
 — «троицы и пятерицы»[48]z:\CorvDoc\infopedia2\shchu01\refer.htm - s49.
— «троицы и пятерицы»[48]z:\CorvDoc\infopedia2\shchu01\refer.htm - s49.
В целом, анализ 22 фрагментов «Цзо чжуани» и «Го юя», содержащих ссылки на гексаграммы, позволяет сделать следующие выводы. В мантических фрагментах «Цзо чжуани» использовано 11 гексаграммных пар, в общетеоретических фрагментах — 9 пар. Во всех этих 20 случаях соотношение гексаграмм в парах основано на общем принципе выделения одной черты посредством противоположной ей черты в той же позиции (19 случаев) или посредством черт, противоположных остальным пяти чертам, в соответствующих позициях другой гексаграммы (1 случай). Последний вариант данного принципа в явном виде сформулирован в синхронном созданию «Цзо чжуани» и «Го юя» методологическом тексте, входящем в состав «Чжоу и», — «Шо гуа чжуани». Оба варианта одновременно реализуются для любой пары противоположных (находящихся в соотношении «супротивности» — дуй) гексаграмм, включенных в 8-гексаграммный набор, по нашему предположению, обозначаемый термином ба — «восемь».
В исследованных мантических фрагментах «Го юя» указаны две пары гексаграмм, различающихся между собой тремя чертами, что явно не соответствует модели «Цзо чжуани», хотя произведения аналогичны друг другу и, по традиционной атрибуции, принадлежат одному автору — ученику Конфуция — Цзо Цю-мину. Одна из этих пар приведена в составе малопонятного выражения дэ чжэнь Чжунь хуй Юй, цзе ба е, отличающегося от стандартной формулы юй А чжи В. Помимо проблематичного термина ба, отнесенного сразу к двум гексаграммам, но далее никак не расшифрованного, здесь гексаграммы загадочно определены терминами чжэнь и хуй, которые в ицзинистике обозначают нижнюю и верхнюю триграммы, образующие единую гексаграмму, что, кстати, отражено в «Цзо чжуани» (Си, 15-й г., зима)[49]z:\CorvDoc\infopedia2\shchu01\refer.htm - s50.
Другая пара гексаграмм в «Го юе» представлена с помощью стандартной формулы — юй Цянь чжи Пи [50]z:\CorvDoc\infopedia2\shchu01\refer.htm - s51, однако и она выглядит подозрительной. Если считать, что эта взаимосвязь Цянь (№1)  и Пи (№12)
и Пи (№12)  основана на трансформации трех «старых» янских черт первой в три «молодые» иньские черты второй гексаграммы, то получается слишком красивый результат, чтобы быть уверенным в его случайном характере. Действительно, ситуация кажется маловероятной: при первом же, наиболее значимом, упоминании в «Го юе» о гексаграммах выпадает гексаграмма №1, в которой изменяющиеся черты следуют друг за другом и охватывают целую нижнюю триграмму, что в итоге рождает одну из важнейших гексаграмм — Пи, сочетающую в себе две главные триграммы — Цянь и Кунь. В мысли об искусственности данного сочетания Цянь и Пи укрепляет также отмеченный выше факт, что именно эта пара стоит в начале мавандуйской последовательности гексаграмм. Указание же на две заглавные гексаграммы китайская научная традиция рассматривает в качестве возможного способа обозначения соответствующей последовательности гексаграмм или излагающего ее текста. Например, упоминавшееся нами сочетание гексаграмм Кунь и Цянь в «Ли цзи» (гл. 9) комментатор Чжэн Сюань (127—200) истолковал как обозначение книги «Гуй цзан»[51]z:\CorvDoc\infopedia2\shchu01\refer.htm - s52.
основана на трансформации трех «старых» янских черт первой в три «молодые» иньские черты второй гексаграммы, то получается слишком красивый результат, чтобы быть уверенным в его случайном характере. Действительно, ситуация кажется маловероятной: при первом же, наиболее значимом, упоминании в «Го юе» о гексаграммах выпадает гексаграмма №1, в которой изменяющиеся черты следуют друг за другом и охватывают целую нижнюю триграмму, что в итоге рождает одну из важнейших гексаграмм — Пи, сочетающую в себе две главные триграммы — Цянь и Кунь. В мысли об искусственности данного сочетания Цянь и Пи укрепляет также отмеченный выше факт, что именно эта пара стоит в начале мавандуйской последовательности гексаграмм. Указание же на две заглавные гексаграммы китайская научная традиция рассматривает в качестве возможного способа обозначения соответствующей последовательности гексаграмм или излагающего ее текста. Например, упоминавшееся нами сочетание гексаграмм Кунь и Цянь в «Ли цзи» (гл. 9) комментатор Чжэн Сюань (127—200) истолковал как обозначение книги «Гуй цзан»[51]z:\CorvDoc\infopedia2\shchu01\refer.htm - s52.
Итак, приемы мантического использования гексаграмм, описанные в «Цзо чжуани» и «Го юе», существенно расходятся. Попытаться объяснить этот странный факт можно исходя из разных предположений. Если считать, что в эпоху Чунь-цю, когда практиковались рассматриваемые гадания, существовала одна система мантического использования гексаграмм, то придется признать более вероятным ее описание в «Цзо чжуани», поскольку содержащийся там однородный материал по своему количеству и качеству намного превосходит малочисленные и подозрительные данные «Го юя». Отличительной характеристикой этой системы гадания является выделение лишь одной особенной черты (по признаку изменяемости или как-то иначе — пока неясно). Аналогичная система была описана великим сунским нумерологом Шао Юном (1011—1077) в трактате «Мэй хуа и шу» 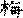
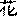
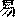
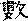 («Числа «Перемен», [открытые] цветением сливы»)[52]z:\CorvDoc\infopedia2\shchu01\refer.htm - s53. Согласно его методу, гексаграмма строится не из отдельных черт, а из триграмм, и в ней, уже после построения, особым вычислением выделяется только одна изменяющаяся черта.
(«Числа «Перемен», [открытые] цветением сливы»)[52]z:\CorvDoc\infopedia2\shchu01\refer.htm - s53. Согласно его методу, гексаграмма строится не из отдельных черт, а из триграмм, и в ней, уже после построения, особым вычислением выделяется только одна изменяющаяся черта.
По-видимому, этот метод в средние века получил достаточное распространение, о чем свидетельствует использование его варианта в сунском астрологическом трактате «Хэ Ло ли шу» 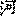
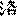
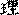
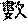 («Принципы и числа [Плана из Желтой] реки [и Писания из реки] Ло»)[53]z:\CorvDoc\infopedia2\shchu01\refer.htm - s54. В частности, там описан алгоритм для получения пары гексаграмм, соотносимой с временем рождения человека (годом, месяцем, днем и двухчасьем). От стандартной гадательной процедуры получения двух гексаграмм этот алгоритм отличается как раз теми особенностями, которые мы выявили на материале «Цзо чжуани» и «Го юя». Во-первых, гексаграммы в нем строятся из триграмм, а не из отдельных черт; во-вторых, взаимосвязь между парными гексаграммами основана на выделении одной черты, а не любого от 0 до 6 их количества; в-третьих, при переходе от первой гексаграммы ко второй изменяются все черты кроме единственной выделенной, а не наоборот, как в мантической практике, где изменяются именно выделенные («старые») черты[54]z:\CorvDoc\infopedia2\shchu01\refer.htm - s55.
(«Принципы и числа [Плана из Желтой] реки [и Писания из реки] Ло»)[53]z:\CorvDoc\infopedia2\shchu01\refer.htm - s54. В частности, там описан алгоритм для получения пары гексаграмм, соотносимой с временем рождения человека (годом, месяцем, днем и двухчасьем). От стандартной гадательной процедуры получения двух гексаграмм этот алгоритм отличается как раз теми особенностями, которые мы выявили на материале «Цзо чжуани» и «Го юя». Во-первых, гексаграммы в нем строятся из триграмм, а не из отдельных черт; во-вторых, взаимосвязь между парными гексаграммами основана на выделении одной черты, а не любого от 0 до 6 их количества; в-третьих, при переходе от первой гексаграммы ко второй изменяются все черты кроме единственной выделенной, а не наоборот, как в мантической практике, где изменяются именно выделенные («старые») черты[54]z:\CorvDoc\infopedia2\shchu01\refer.htm - s55.
Выявленные параллели позволяют предполагать, что разбираемый метод не был создан в эпоху Сун (X—XIII вв.), а существовал уже задолго до нее, во времена Чунь-цю наряду с другим или другими методами. Если отказаться от этого предположения и признать, что тогда была в ходу лишь одна-единственная система гадания посредством гексаграмм, то возникает затруднительное положение с объяснением соответствующих мантических фрагментов «Го юя». Кроме того, в тексте, синхронном созданию «Цзо чжуани» и «Го юя», — «Си цы чжуани» (I, 8/9) дано описание построения гексаграммы, издревле толкуемое комментаторами с помощью чисел 6, 7, 8, 9, т.е. как предполагающее возможность получения нескольких изменяющихся черт.
Эти трудности легко преодолимы при допущении одновременного существования двух или более систем мантического использования гексаграмм. В таком случае окажется, что в «Цзо чжуани» отражена система типа описанной Шао Юном, а в «Го юе» — типа описанной в «Си цы чжуани». Весьма вероятно также, что каждой системе соответствовал собственный порядок гуа (три- и гексаграмм), что представлено в «Чжоу ли» как применение при великом гадании «приемов трех Перемен»: «Смыкающихся гор», «Возвращения в сокровищницу» и «Всеохватно-круговых (Чжоуских) перемен».
В нумерологических схемах гуа располагаются в линию, квадратом (символ земли), соотносясь по вертикали, горизонтали и диагонали, а также кругообразно (символ неба), соотносясь по окружности и через центр (отношения цзун 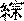 и цо
и цо 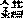 ); делятся на «мужские» и «женские»; образуют пары по двум главным принципам: «обратности» (фань
); делятся на «мужские» и «женские»; образуют пары по двум главным принципам: «обратности» (фань 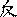 ), т.е. перевернутости членов пары относительно друг друга на 180º (например,
), т.е. перевернутости членов пары относительно друг друга на 180º (например,  и
и 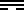 ), и «супротивности» (дуй
), и «супротивности» (дуй 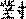 ), т.е. противоположности черт в одинаковых позициях (например,
), т.е. противоположности черт в одинаковых позициях (например, 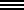 и
и  ). Эти два вида противопоставления[55]z:\CorvDoc\infopedia2\shchu01\refer.htm - s56 в традиционной китайской методологии охватывают все контрарные и контрадикторные отношения, т.е. и противоположность и противоречие.
). Эти два вида противопоставления[55]z:\CorvDoc\infopedia2\shchu01\refer.htm - s56 в традиционной китайской методологии охватывают все контрарные и контрадикторные отношения, т.е. и противоположность и противоречие.
Кроме того, они выражают два универсальных закона мироздания, синтезируемых в понятии дао. Сам исходный смысл иероглифа дао — «путь» — двуедин: путь — это и статический объект, дорога, и динамический процесс, движение по дороге. Соответственно наиболее общие определения дао выделяют в нем и универсальную статическую структуру «супротивности» в виде бинарной оппозиции сил инь и ян, и универсальный процесс «обращения вспять» в виде перехода от одного члена оппозиции к другому и наоборот: «Одна инь, один ян — это называется дао» («Си цы чжуань», I, 5)[56]z:\CorvDoc\infopedia2\shchu01\refer.htm - s57; «Обозначая иероглифом, говорим: это — дао... о [нем] далекоидущем говорим: обратное (фань)» («Дао дэ цзин», §25)[57]z:\CorvDoc\infopedia2\shchu01\refer.htm - s58; «Дао есть то, благодаря чему происходит обращение (фань) к корню и возвращение к началу» («У-цзы», гл. I)[58]z:\CorvDoc\infopedia2\shchu01\refer.htm - s59.
В динамическом плане взаимопревращения гуа (путем трансформации черт в противоположные) отражают все фазы циклического развития космоса в основополагающей для «Чжоу и» теории кругообразных перемен (чжоу и). В статике целая и прерванная черты гексаграмм обозначаются цифрами 9 и 6. Объяснение этого шифра, по мнению академика В.М. Алексеева, является «едва ли не основным» для понимания «Чжоу и»[59]z:\CorvDoc\infopedia2\shchu01\refer.htm - s60. В динамике (при мантическом построении) каждая из двух черт еще дифференцируется по двум состояниям — «старости» (лао) и «молодости» (шао). В результате образуются четыре элемента (сы сян), выражаемые числовыми и графическими символами: «старая инь» — 6,  («переплетенная» — цзяо), «молодая инь» — 8
(«переплетенная» — цзяо), «молодая инь» — 8  , («переломленная» — чжэ), «молодой ян» — 7
, («переломленная» — чжэ), «молодой ян» — 7  , («одинарный» — дань), «старый ян» — 9
, («одинарный» — дань), «старый ян» — 9  , («повторенный» — чун). Первый и последний элементы могут трансформироваться в противоположные по принципу: инь переходит в ян, ян — в инь [60]z:\CorvDoc\infopedia2\shchu01\refer.htm - s61.
, («повторенный» — чун). Первый и последний элементы могут трансформироваться в противоположные по принципу: инь переходит в ян, ян — в инь [60]z:\CorvDoc\infopedia2\shchu01\refer.htm - s61.
Используемые для описания трансформаций гексаграмм четыре «формирующих» числа 6, 7, 8, 9[61]z:\CorvDoc\infopedia2\shchu01\refer.htm - s62, на наш взгляд, производны от геометрической структуры триграмм. Последние традиционно изображаются в квадратной форме и в «Си цы чжуани» (I, 11) прямо определены термином фан («квадрат»)[62]z:\CorvDoc\infopedia2\shchu01\refer.htm - s63. В таком квадрате должно быть три строки (по количеству черт триграммы) и три столбца (в силу трехчастности каждой черты, что явствует из сопоставления целой и прерванной черт: 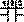 ), т.е. он должен быть девятиклеточным 3x3 (что определяется термином
), т.е. он должен быть девятиклеточным 3x3 (что определяется термином 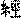 цзин — «канон»)[63]z:\CorvDoc\infopedia2\shchu01\refer.htm - s64. При вписывании в него всех восьми триграмм образуются четыре комбинации, разнящиеся числом заполненных и пустых клеток (см. схему 13). Цифры, выражающие количество заполненных клеток в этих комбинациях, оказываются именно 6, 7, 8, 9.
цзин — «канон»)[63]z:\CorvDoc\infopedia2\shchu01\refer.htm - s64. При вписывании в него всех восьми триграмм образуются четыре комбинации, разнящиеся числом заполненных и пустых клеток (см. схему 13). Цифры, выражающие количество заполненных клеток в этих комбинациях, оказываются именно 6, 7, 8, 9.
Главные в данной четверке цифры 9 и 6 предстали индексами главных триграмм Цянь и Кунь. В силу полной однородности черт в этих триграммах их числовые символы 9 и 6 могли быть перенесены с целого на часть и присвоены чертам ян и инь как простейшим эквивалентам Цянь и Кунь.
Остальные шесть триграмм на схеме 13 образовали две группы по три, представляемые цифрами 7 и 8. Следовательно, соотношение «старых» и «молодых» триграмм оказалось равным 1 к 3, что точно соответствует соотношению вероятностей получения стандартных числовых символов «старых» (9, 6) и «молодых» (7, 8) черт гексаграмм при гадании обоими классическими способами, как с помощью 50 стеблей тысячелистника: 9 — 3/16, 6 — 1/16, 7 — 5/16, 8 — 7/16, так и с помощью трех монет: 9 — 1/8, 6 — 1/8, 7 — 3/8, 8 — 3/8[64]z:\CorvDoc\infopedia2\shchu01\refer.htm - s65. Хотя вероятности получения указанных чисел при более авторитетном гадании с помощью стеблей тысячелистника отличаются от таковых в монетном варианте, суммарные вероятности «старых» и «молодых» там и тут совершенно одинаковы, соотносясь друг с другом, как 1 и 3:
| состояние черт гексаграмм | числовые символы черт гексаграмм | вероятность получения с помощью стеблей тысячелистника | вероятность получения с помощью монет |
| «старые» «молодые» | 9+6 7+8 | 3/16+1/16=1/4 5/16+7/16=3/4 | 1/8+1/8=1/4 3/8+3/8=3/4 |
Кроме того, объединенные на схеме 13 цифрами 7 и 8 тройки триграмм объединены в «Шо гуа чжуани» (§10-11) как три «сына (мужчины)» и три «дочери (женщины)»[65]z:\CorvDoc\infopedia2\shchu01\refer.htm - s66. Старший, средний и младший «сын» (Чжэнь, Кань, Гэнь) соотнесены с «отцом» (Цянь), что вполне совпадает со связью 7 — 9; старшая, средняя и младшая «дочь» (Сюнь, Ли, Дуй) соотнесены с «матерью» (Кунь), что вполне совпадает со связью 8 — 6. Каждая из «сыновних» и «дочерних» триграмм скоординирована с одной из черт «отцовской» или «материнской» триграммы (старшая — с нижней, средняя — с центральной, младшая — с верхней) соответственно наличию такой же черты в данной позиции, и в целом вся эта система образует линейную последовательность триграмм, приписываемую Вэнь-вану. Ее структура, судя по результатам нашего анализа, закономерно связана с мантической числовой символикой и представляет собой нумерологическую интерпретацию наложения триграмм на канонический девятиклеточный квадрат (цзин).
Связь триграмм с девятиклеточным квадратом прослеживается и еще по одной линии. В стандартном двухмерном расположении триграммы занимают восемь клеток такого квадрата (незаполненной в нем остается центральная клетка). Если в девятиклеточном квадрате с расположением триграмм, приписываемым Фу-си (см. схему 6), вместо триграмм поставить их числовые эквиваленты, показанные на схеме 13, то каждая из четырех пар диаметрально расположенных величин даст в сумме 15 (см. схему 14), что равно константной сумме троек чисел в девятиклеточном магическом квадрате Ло шу — «Писании [из реки] Ло» (см. схему 17). Если в этом же расположении вместо триграмм поставить другие соотносимые с ними числа, образуемые суммами числовых значений их черт (целая — 9, прерванная — 6), то каждая из четырех пар диаметрально расположенных величин даст сумму 45 (см. схему 15), которая также коррелирует с Ло шу, равняясь сумме всех его чисел.
После общего обзора основных принципов организации гуа рассмотрим несколько более подробно систему их пространственных расположений, поскольку вместе с «магическим крестом» Хэ ту — «Планом [из Желтой] реки» (см. схему 16), магическим квадратом Ло шу — «Писанием [из реки] Ло» (см. схему 17) и системой пространственных расположений пяти элементов она образует фундамент нумерологической символистики[66]z:\CorvDoc\infopedia2\shchu01\refer.htm - s67. Комментаторская традиция «Чжоу и» выделяет две главные линейные (цы сюй) последовательности триграмм (ЛПТ), связываемые с именами Фу-си (ЛПТФС) и Вэнь-вана (ЛПТВВ): ЛПТФС — Цянь, Дуй, Ли, Чжэнь, Сюнь, Кань, Гэнь, Кунь; ЛПТВВ — Цянь, Кунь, Чжэнь, Кань, Гэнь, Сюнь, Ли, Дуй. В первой мужскими считаются триграммы Цянь, Ли, Сюнь, Гэнь, женскими — Дуй, Чжэнь, Кань, Кунь; во второй мужскими — Цянь, Чжэнь, Кань, Гэнь, женскими — Кунь, Сюнь, Ли, Дуй[67]z:\CorvDoc\infopedia2\shchu01\refer.htm - s68.
Кроме них в источниках встречаются и другие последовательности. Например, в «Шо гуа чжуани» (§3-11)[68]z:\CorvDoc\infopedia2\shchu01\refer.htm - s69 приведены шесть последовательностей: 1) Цянь, Кунь, Гэнь, Дуй, Чжэнь, Сюнь, Кань, Ли (§3), 2) Чжэнь, Сюнь, Кань, Ли, Гэнь, Дуй, Цянь, Кунь (§4), 3) Чжэнь, Сюнь, Ли, Кунь, Дуй, Цянь, Кань, Гэнь (§5), 4) Чжэнь, Сюнь, Ли, Дуй, Кань, Гэнь (§6), 5) Кань, Ли, Чжэнь, Сюнь, Гэнь, Дуй (§6), 6) Цянь, Кунь, Чжэнь, Сюнь, Кань, Ли, Гэнь, Дуй (§7-11).
Но все они, как, впрочем, и ЛПТФС с ЛПТВВ, производны от квадратно-круговых расположений триграмм (КРТ), в которых триграммы размещаются равномерно по периметру квадрата или окружности (фан вэй). Таковых традиция «Чжоу и» выделяла опять-таки два — «преднебесное» (сянь тянь) и «после-небесное» (хоу тянь), связывая их с именами все тех же Фу-си и Вэнь-вана: первое (КРТФС) воспроизведено на схеме 6, второе (КРТВВ) — на схеме 7. На обеих схемах осями разделены четверки триграмм, считающиеся женскими и мужскими в данных расположениях. Сравнение по этому признаку их между собой, а также с ЛПТФС и ЛПТВВ хорошо демонстрирует функциональную амбивалентность триграмм, меняющих свои качества даже на противоположные в зависимости от образуемой ими символизационной системы (в данном случае неизменными в своих признаках оказались только мужская триграмма Цянь и женская Кунь, поскольку они являются исходными точками отсчета).
КРТВВ прямо зафиксировано в «Шо гуа чжуани» (§5, 6), его полным и сокращенным описанием являются воспроизведенные оттуда последовательности 3) и 4), которые задают периметрально-кольцевой (цзун) способ считывания элементов этой системы. В §5 «Шо гуа чжуани» не только указаны взаиморасположение триграмм и порядок перехода от одной к другой, но и дана их увязка со странами света (на соответствующих схемах, следуя китайской топографической традиции, мы соотносим юг с верхом, север с низом, восток с левой стороной, запад с правой), в частности, начальная Чжэнь отнесена к востоку.
Остальные воспроизведенные выше последовательности триграмм из «Шо гуа чжуани» комментаторы «Чжоу и» считали описанием КРТФС. Как показал проведенный нами специальный анализ[69]z:\CorvDoc\infopedia2\shchu01\refer.htm - s70, они когерентны, т.е. образуют единую систему, и, действительно, структурно связаны с КРТФС. Во всяком случае несомненно, что, описывая эти последовательности, автор «Шо гуа чжуани» имел перед глазами или мысленным взором какое-то квадратно-круговое расположение триграмм, аналогичное отраженному в §5 и 6. Общая идея квадратно-кругового расположения гуа передана в «Чжоу и» их определением термином фан («квадрат»), заключающем в себе представление о концентрическом двухмерном пространстве в виде многоугольника с количеством сторон, кратным 4 («Си цы чжуань», I, 11)[70]z:\CorvDoc\infopedia2\shchu01\refer.htm - s71. Кроме того, в четырех разбираемых последовательностях — 1), 2), 5), 6) — триграммы указаны стабильными парами, а в §3 «Шо гуа чжуани» такая парность квалифицирована как «взаимное перекрещивание» (сян цо), т.е. соотношение друг с другом через центр. Именно оппозиционность через центр (сян дуй) характерна для КРТФС.
Но все же графические изображения КРТФС известны лишь с эпохи Сун, поэтому теоретически можно допустить, что квадратно-круговое расположение триграмм, отвечающее принципу цо и отраженное в §3, 4, 6-11 «Шо гуа чжуани», по своей сути аналогично КРТФС, но в деталях отличается от него. Единственным претендентом на эту роль пока является пространственное расположение триграмм, реконструируемое из мавандуйской линейной последовательности гексаграмм. Последняя образована посредством двух последовательностей триграмм: верхних — Цянь, Гэнь, Кань, Чжэнь, Кунь, Дуй, Ли, Сюнь, каждая из которых в гексаграммах занимает по восемь позиций подряд (ВЛПТМВД), и нижних — Цянь, Кунь, Гэнь, Дуй, Кань, Ли, Чжэнь, Сюнь, каждая из которых чередуется через восемь позиций (НЛПТМВД). Эту закономерность видоизменяет одно правило: в каждой восьмерице гексаграмм первым стоит удвоение «возглавляющей» ее триграммы верхней последовательности, что начиная со второй восьмерицы приводит к соответствующим сдвигам в нижней последовательности (см. схему 11).
Анализ данной структуры позволяет предположить, что мавандуйская последовательность гексаграмм была получена с помощью простого приспособления, имеющего аналоги среди древнекитайских астрономо-астрологических инструментов и ритуальных предметов. Оно (КРТМВД) должно было представлять собой круг, в котором по странам и полустранам света располагались триграммы нижней последовательности, и окружающее его кольцо, в котором точно так же располагались триграммы верхней последовательности (см. схему 18). Путем их вращения относительно друг друга и поочередного совмещения каждой из верхних триграмм с восемью нижними можно механически получить мавандуйскую последовательность гексаграмм. С помощью подобного приспособления из КРТФС выводятся соответствующие последовательность и расположение гексаграмм, с той только разницей, что верхняя и нижняя последовательности триграмм тут идентичны и вращение идет не в одну сторону, а меняет свое направление на противоположное после прохождения половины окружности.
Как мы установили, сходный инструмент, основанный на этой же идее механического сочетания терминов, нанесенных на вращающиеся относительно друг друга концентрические круги и кольца, очевидно, использовался в комбинаторной практике, связанной с системой пяти элементов. Таким образом, в нумерологии был выработан принцип нумерологической машины, типологического аналога первой в Европе логической машины Раймунда Луллия (1235—1315). В данном случае не исключено и знакомство последнего с более древней китайской конструкцией через посредство мусульманской культуры, великолепным знатоком которой он был. Однако реальный теоретический параллелизм в решении нумерологических и логических задач тут, пожалуй, интереснее, чем возможные исторические взаимовлияния.






