Лабораторная работа №101
(для не физиков)
Изучение законов столкновения тел.
Принадлежности: прибор для исследования столкновения шаров ЛТЭ, набор шаров (стальные).
Цель работы: экспериментальная проверка выполнения закона сохранения импульса при столкновении шаров.
Введение. В механике, под ударом следует понимать кратковременное взаимодействие двух или более тел, возникающее в результате их соприкосновения.
Абсолютно упругий удар.
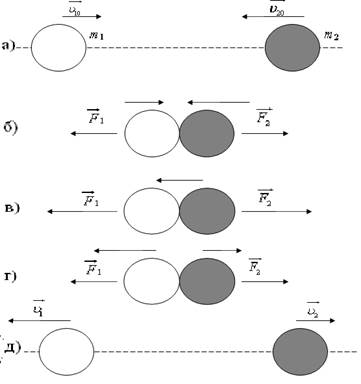Если в результате удара механическая энергия не переходит в другие формы энергии, то удар называется абсолютно упругим. При упругом ударе соударения двух тел, например, двух костяных или стальных твердо закаленных шариков, происходит упругая деформация шариков, поверхности соударяющихся тел вдавливаются и сила давления, вследствие деформации шариков, изменяет их скорость. Анализ явлений, имеющих место при ударе упругих сплошных тел, довольно сложен. Рассмотрим самый простой случай – центральный удар двух однородных шаров. Центральным называют такой удар, при котором скорости соударяющихся шаров до удара совпадают по направлению с линией, соединяющей центры масс шаров (рис 1а). Эта прямая линия называется линией центров. Процесс соударения происходит примерно следующим образом. Во время сближения шаров (рис.1б) силы, действующие на них (
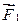и 
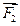), увеличиваются с увеличением деформации, пока скорости обоих шаров не сравняются (рис. 1в). В этот момент деформации достигают максиму Рис. 1
ма, а затем они начинают уменьшаться, при этом силы деформации расталкивают шары (рис. 1г) до тех пор, пока они не разойдутся; далее шары будут двигаться с различными скоростями (рис.1д).
Если удар можно считать абсолютно упругим, то для скоростей до и после удара должны быть справедливы уравнения, выражающие закон сохранения импульса и закон сохранения энергии.
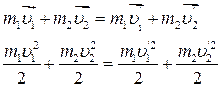(1)
Уравнение (1) в случае центрального удара можно рассматривать как скалярное (все скорость до и после удара направлены по линии центров и их разные направления различаются только знаком) и переписать его в виде
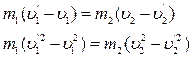(2)
где υ1 и υ2 – скорости шаров до удара, а υ’1 и υ’2 – скорости их после удара.
Разделив второе уравнение на первое, получим:
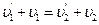(3)
Умножая это уравнение один раз на m 2, а другой раз на m 1 и вычитая его из уравнения (2), получим выражение для обеих скоростей после удара:
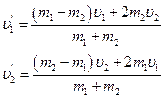(4)
В общем виде эти выражения сложны. Мы рассмотрим только два частных случая, охватываемых этими соотношениями.
1) Сумма импульсов обоих шаров до удара равна нулю, т.е.
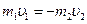(5)
Тогда уравнения (4) принимают вид
, 
,
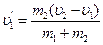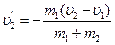Откуда, применяя (5), находим
, 
,
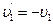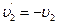т. е. импульсы обоих шаров при ударе только изменяют свой знак. Результат этот почти очевиден. Так как по закону сохранения импульса оба импульса после удара должны быть также равны по величине и противоположны по знаку, а по закону сохранения энергии они при этом не должны изменять своей абсолютной величины, то они могут только изменить знаки на обратное.
2) один шар до удара покоился: υ2=0. тогда
, 
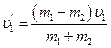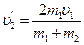
После удара второй шар движется в ту же сторону, куда двигался первый до удара. Скорость υ’2 и поведение первого шара зависит от соотношения масс.
а) Если m 1> m 2, то первый шар продолжает двигаться в том же направлении, как и до удара, но с меньшей скоростью. Скорость второго шара после удара больше, чем скорость первого до удара (рис. 2).
б) Если m 1< m 2, то направление движения первого шара при ударе изменится – шар отскакивает обратно. Второй шар движется в ту сторону, в которую двигался первый до удара, но с меньшей скоростью (рис. 3).
в) Массы шаров одинаковы: m 1= m 2. Тогда
, 
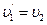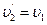
т.е. шары равной массы при ударе обмениваются скоростями.
Рис. 2. Рис. 3.
Абсолютно неупругий удар
Интересным примером, где имеет место потеря механической энергии под действием диссипативных сил, является абсолютно неупругий удар. Так называется столкновение двух тел, в результате которого они соединяются вместе и движутся дальше как одно тело. Примером может служить столкновение шаров из пластилина или глины.
Физически явления при столкновении тел довольно сложны. Сталкивающиеся теля деформируются, возникают упругие силы и силы трения, в телах возбуждаются колебания и волны и т. д. Однако, если удар неупругий, то, в конце концов, все эти процессы прекращаются, и в дальнейшем оба тела, соединившись вместе, движутся как единое твердое тело. Его скорость можно найти, не вдаваясь в механизм явления, а используя только закон сохранения импульса.
Пусть шары движутся вдоль прямой, соединяющей их центры масс, со скоростями υ1 и υ2. Обозначим через υ общую скорость шаров после столкновения. Закон сохранения импульса дает
,
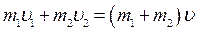где m 1 и m 2 – массы шаров. Отсюда получаем
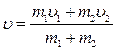
Кинетические энергии системы до удара и после удара равны соответственно
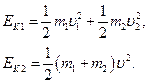
Пользуясь этими выражениями нетрудно получить
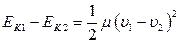
где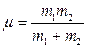 
– приведенная масса шаров.
Таким образом, при столкновении двух абсолютно неупругих шаров происходит потеря кинетической энергии макроскопического движения, равная половине произведения приведенной массы на квадрат относительной скорости.
Определение скорости шаров при соударении.
Эксперимент состоит в определении количества движения шаров до и после столкновения.Согласно закону сохранения энергии механическая энергия изолированной системы во время движения системы не изменяется. Импульс шаров до столкновения определяется по формуле
Р = m1υ1, (1)
Где m1 –масса ударяющего шара (шар №1), υ1 – скорость шара№1
Шар, отведенный из положения равновесия на угол α (рис.4) обладает запасом потенциальной энергии Еп=m1gh. Эта энергия в начальный момент соприкосновения полностью переходит в кинетическую энергию
,
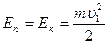Откуда
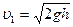(2)
Для определения высоты h рассмотрим тригонометрические соотношения в треугольнике АВС:
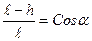
Откуда
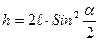
Подставив h в уравнение (2), получим:
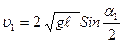(3)
Где g– ускорение свободного падения, ℓ- длина подвески, α- начальный угол отклонения шара от положения равновесия.
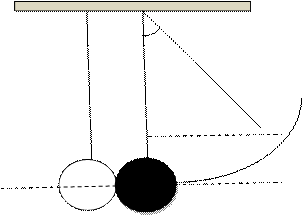
Рис.4.
Суммарное количество движения шаров после упругого столкновения определяется по формуле:
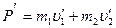(4)
Где m2 – масса ударяемого шара,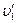 
- скорость ударяющего шара после столкновения, 
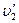- скорость ударяемого шара после столкновения. Скорост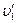и и 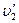определяются по формулам
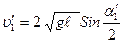(5)
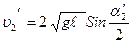(6)
Где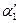 
- угол, на который после столкновения отскочил ударяющий шар, 
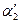- угол, на который после столкновения отскочил ударяемый шар.
Описание установки.
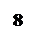
Рис.5
Для проведения лабораторной работы используется установка ЛТЭ рис.5. Установка состоит из механического блока 1 БМ2-02 и электронного секундомера 8 СЭ1 -8. Механический блок включает в свой состав основание 1, держатель нити 2, регулятор длины нити 3, электромагнит 4, шар№1 и шар№2- 5, указатель отклонения шара №1 -6, указатель отклонения шара №2 -7.
Электромагнит 4 служит для фиксации шара. Электромагнит отключается при нажатии кнопки «Пуск» секундомера 8. Включение секундомера производится кнопкой «Сеть».
Измерения.
1. Включить секундомер в сеть. Установить на секундомере режим 2.
2. Подвесить шарик 5 (рис.2) к электромагниту 4.Установить угол α=600 (начальный угол отклонения шара от положения равновесия).Контроль угла осуществляется с помощью указателя 6. Указатель 7 установить на нулевое положение.
3. Нажать кнопку «Пуск» секундомера. Провести измерения угла α2 на который после столкновения отскочит ударяемый шар. Данные записать в таблицу 1.
4. Повторить измерения для углов α=500,400,300,200.Для каждого угла проводится одно измерение.
5. Определить длину подвески шаров (расстояние между стержнем верхнего кронштейна и центром шара).
6. Используя весы определить массы m1 и m2шаров.
Обработка результатов измерений.
1. По формуле (3) определить скорость ударяющего шара(шар№1).
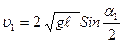
2. По формуле (1) определить импульс шаров до удара.
Р = m1υ1
3. По формуле определить скорость ударяемого шара (шар№2)после столкновения
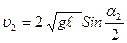
4.Определить импульс шаров после упругого столкновения по формуле
5. Сравнить значения Р и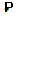 
до и после столкновения. Записать вывод о характере столкновения шаров.
Таблица.
| № | α1 | α2 | υ1 | υ2 | Р | 
|
| 600 | ||||||
| 500 | ||||||
| 400 | ||||||
| 300 | ||||||
| 200 |
Контрольные вопросы.
1. Что такое импульс системы материальных точек и как он изменяется под воздействием внешних сил?
2. Сформулируйте закон сохранения импульса. Для каких систем он справедлив? Почему к явлению удара можно применить закон сохранения количества движения?
3. Что называют кинетической и потенциальной энергией? Каковы особенности этих видов энергий?
4. Сформулируйте закон сохранения механической энергии. В каких случаях полная механическая энергия системы не сохраняется? Почему в данной работе можно применить закон сохранения энергии?
5. Какие виды ударов шаров известны вам? В каких случаях не выполняется закон сохранения механической энергии? Какой удар называется центральным?
6. Как определить скорости тел после центрального абсолютно упруго удара? Следствием каких законов являются эти выражения?
7. Как определяется скорость шаров? Вывод формулы.
Список рекомендуемой литературы
1. Савельев И. В. Курс общей физики. В 3-х т. М.: Наука, 1977. Т I.
2. Детлаф А. А., Яворский Б. М., Милковская Л. Б. Курс физики. В 3-х т. М.: Высшая школа, 1973. Т. 1.
3.СтрелковС.П. Механика. СПб.:Лань,2005.
4.Сивухин Д.В. Общий курс физики. Т.1.Механика. М.:Физматлит.2006.
5.Трофимова Т.И.Курс физики, М.:Академия, 2006.
